三项式xn-bx+a的二次不可约因式

吴华明

(湛江师范学院数学与计算科学学院，广东湛江 524048)

三项式xn-bx+a的二次不可约因式

吴华明*

(湛江师范学院数学与计算科学学院，广东湛江 524048)

三项式； 二次不可约因式； Lucas数； 本原素因数

设n是大于1的正整数，f(x)=xn-bx+a，其中a,b是非零整数.三项式f(x)在有理数域的可约性和因式分解在代数学及其应用领域有着重要的意义[1].根据Gauss引理可知：如果f(x)在有理数域上可约，则f(x)可表成2个次数都小于n且首项系数等于1的整系数多项式的乘积(参见文献[2]的定理1.13.2).本文主要讨论f(x)的首项系数等于1的二次整系数不可约因式(以下简称二次因式)的存在性.对此，陈宏基[3]证明了：当b=1且n>512 880时，如果f(x)有二次因式，则必有

n≡2(mod 6),a=1,b=1,g(x)=x2-x+1.

(1)

(2)

上述结果的证明要用到有关代数数对数线性型的下界估计.这里应该指出：当a=1,b=-1,n≡5(mod 6)时，因为x3≡-1(modx2-x+1)，故有f(x)≡-x2+x-1≡0(modx2-x+1),由此可知文献[5]遗漏了以下情况

n≡5(mod 6),a=-1,b=-1,g(x)=x2-x+1.

(3)

本文将运用有关Lucas数本原素因数的存在性方面的结果，修正并改进文献[5]得到的下界，即证明了：

1 若干引理

设g(x)=x2-sx+t是整系数二次多项式，又设r=s2-4t.已知g(x)在有理数域上不可约的充要条件是r为非平方整数.此时，g(x)有2个不同的根

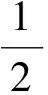
(4)

对于非负整数k，设

(5)

引理1[6]设m是正整数，u和v是任意复数.此时

对此，教师在平时的教学中可以让学生在阅读时养成积累写作素材的好习惯，调动学生写作的积极性，让学生能够在写作的过程中大胆进行创新，展示自我，另外，教师也要对学生的写作进行适当的鼓励，让学生逐渐喜欢上写作，培养其写作的积极性，增加写作和阅读的热情。

其中[m/2]表示m/2的整数部分，

都是正整数.

引理2 设d=gcd(s,t).当k是正整数时，Lk(α,β)是适合

Lk(α,β)≡0(modd[k/2])

(6)

的非零整数.

证明因为α≠β，所以当k是正整数时，Lk(α,β)≠0.由于d=gcd(s,t)，故有

r=dr1,s=ds1,t=dt1,

(7)

其中r1,s1,t1都是非零整数.当k是奇数时，根据引理1，从式(4)可知

(8)

从式(7)和式(8)可知此时式(6)成立.当k是偶数时，k可表成k=2lk1，其中l是正整数，k1是正奇数.此时，因为

(9)

所以根据引理1也可推出式(6).证毕.

引理3f(x)有二次因式g(x)的充要条件是b=Ln(α,β).

引理3的证明可参见文献[5]的引理3，在此略.

当gcd(s,t)=1且α/β不是单位根时，(α,β)称为一个Lucas对.此时，Lk(α,β)称为与Lucas对应的Lucas数.当k是大于1的正整数时，如果Lk(α,β)的素因数p不能整除tL1(α,β)…Lk-1(α,β)，则称p是Lk(α,β)的本原素因数.

引理4 当k>30时，Lucas数Lk(α,β)必有本原素因数.

引理5 如果p是Lucas数Lk(α,β)的本原素因数，则必有p≡±1(mod 2k).

引理4和引理5的证明可分别参见文献[7]、文献[8]，在此略.

2 定理的证明

设g(x)是f(x)的二次因式.根据文献[5]中定理的证明过程以及本文的分析可知：当α/β是单位根时，n,a,b必定满足式(1)、(2)或(3).因此，以下仅需考虑α/β不是单位根的情况.

设n是适合

(10)

的正整数，又设d=gcd(s,t).当d>1时，根据引理2可知

(11)

同时，从引理3可知

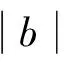
(12)

结合式(11)和(12)立得

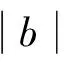
(13)

与式(10)矛盾，故不可能.

当d=1时，(α,β)是Lucas对，Ln(α,β)是相应的Lucas数.因为n>30，所以从引理4可知Ln(α,β)必有本原素因数p，故有

(14)

又从引理5可知p≥2n-1，故从式(14)立得

(15)

[1] 刘木兰.数学在密码中的某些应用[J].数学的实践与认识，1986，16(3):47-55.

[2] 华罗庚.数论导引[M].北京：科学出版社，1979:19-20.

[3] 陈宏基.关于三项式xn-x-a的二次因式[J].数学杂志，2002，22(3):319-322.

CHEN Hongji.On the quadratic factorization ofxn-x-a[J].Journal of Mathematics,2002,22(3):319-322.

[4] 乐茂华.三项式xn-x-a的二次不可约因式[J].数学杂志，2004，24(6):635-637.

LE Maohua.The irreducible quadratic factor of the trinomialxn-x-a[J].Journal of Mathematics,2004,24(6):635-637.

[5] 杨仕椿.关于三项式xn-bx-a的二次整系数因式[J].南京大学学报:数学半年刊，2004，21(1):178-183.

YANG Shichun.On the intergral coefficient quadratic factorization ofxn-bx-a[J].Journal of Nanjing University:Mathematical Biquarterly,2004,21(1):178-183.

[6] LIDI R,NIEDERREITER H.Finite fields[M].Massachusetts: Addison-Wesley,1983:176-178.

[7] BILU Y,HANROT G,VOUTIER P M.Existence of primitive divisors of Lucas and Lehmer numbers[J].J Reine Angew Math,2001,539:75-122.

[8] LEHMER D H.An extended theory of Lucas’ functions[J].Ann Math,1930,31:419-448.

Keywords： trinomial； irreducible quadratic factor； Lucas number； primitive divisor

【责任编辑 庄晓琼】

THEIRREDUCIBLEQUADRATICFACTORSOFTHETRINOMIALxn-bx+a

WU Huaming

(School of Mathematics and Computation, Zhanjiang Normal University, Zhanjiang, Guangdong 524048, China)

2010-06-01

国家自然科学基金项目(10771186,10971184)

*通讯作者,wuhuam3329@126.com

1000-5463(2011)02-0046-03

O156.7

A