基于巨磁阻抗效应表征材料磁结构的模型*
方允樟, 范晓珍
(浙江师范大学 数理与信息工程学院,浙江 金华 321004)
基于巨磁阻抗效应表征材料磁结构的模型*
方允樟, 范晓珍
(浙江师范大学 数理与信息工程学院,浙江 金华 321004)
研究了一种可用于磁结构表征的基于巨磁阻抗效应分析材料磁结构的模型.在建立巨磁阻抗效应与简化磁结构对应关系模型的基础上,结合磁化矢量正交分解手段,通过调节巨磁阻抗效应与简化磁结构对应关系模型特征参量的方法,获得了各种形状的巨磁阻抗曲线,根据拟合得到的解叠子谱特征,可获知材料内部磁结构的组成和特征.研究结果对于磁性材料内部磁结构的新型表征方法及其内部结构的控制具有重要的意义.
磁结构;巨磁阻抗效应;磁化矢量;计算机拟合;模型
0 引 言
磁结构的测量是一个常青的研究课题,为了更有效地提高和控制磁性材料的性能,以满足不断发展的应用需求,如何更有效、更灵敏、更准确和更简便地测量磁性材料内部的磁结构,一直是全世界磁结构研究者不懈探索的一个基本课题.粉纹法[1-2]和克尔磁光效应法[3-4]是人们常用的比较简便的磁结构测量方法,但这2种方法由于不能直接给出磁性材料的内部磁结构和测量精度不够高而难以满足不断深入的研究需求.磁力显微镜是继原子力显微镜后发展起来的一种新型磁结构测量手段[5-8],相比前2种手段,它大幅度提高了磁结构的分辨率,成为当前磁结构测量的先进手段.但是磁力显微镜仍然存在不尽人意的地方,它同样与前2种方法一样,只能直接给出材料表面磁结构的信息,无法直接给出磁性材料的内部磁结构.另外,这些当前常用的磁结构观测方法,对样品表面的平整度有较高的要求,除了用来观察薄膜样品表面磁结构的情况外,大多数样品表面的平整度通常都不符合要求,需要进行表面处理,而这种处理过程除了使测量过程变得复杂、不够简便外,还往往会使被观测样品的磁结构改变,导致被测结果的不可靠.因此,人们一直期待着有一种更有效、更灵敏、更准确和更简便的磁结构测量方法.巨磁阻抗(Giant Magneto-impedance,简称GMI)效应[9]是一种对材料内部磁结构十分敏感的效应.大量研究结果表明,材料内部磁结构的变化会显著地改变GMI效应[10-15].反过来,材料的GMI效应能灵敏地反映出材料本身的磁结构.因此,人们预言:GMI效应将成为一种很有前途的新型磁结构表征方法[16].然而,相关研究还未见报道.本文从GMI曲线出发,根据纯横向易磁化结构和纯纵向易磁化结构的2个理想化简单磁结构模型,采用计算机拟合的方法对GMI曲线进行拟合,并对模型中各组成部分特征参量进行调整,获得了各种形状的GMI曲线,根据GMI拟合曲线得到的解叠子谱特征,可获知材料内部磁结构组成,这对磁结构测量新方法和磁性材料的制备工艺研究具有指导意义.
1 GMI曲线与理想化简单磁结构对应模型
1.12种理想化简单磁结构模型
1.1.1 纯横向易磁化结构模型
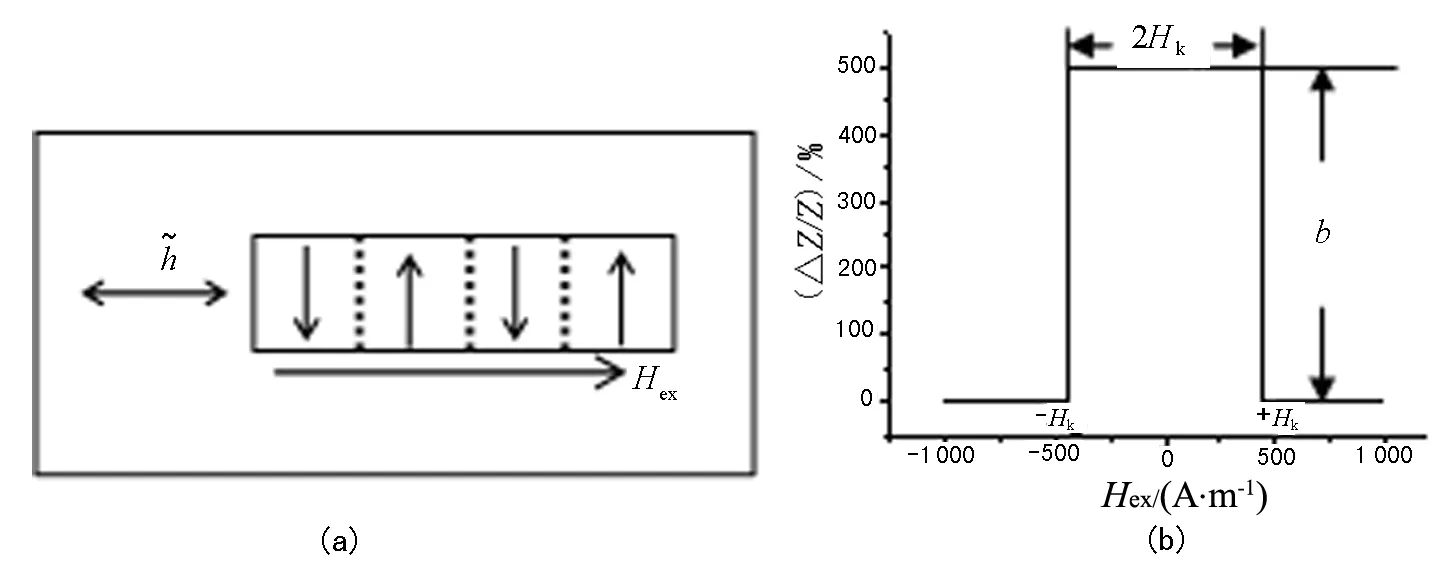
图1 理想化的纯横向易磁化结构模型及对应的GMI曲线
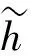
纯横向易磁化结构模型整齐划一的磁化行为,虽然图像清晰、简单明了,但是过于简化,与实际材料的磁化行为偏离太大,需要进行修正.在实际材料中,磁结构不可能完全一致,不可能呈现整齐划一的磁化行为,而是不可避免地存在磁结构的不均匀性.假设这种不均匀性服从高斯统计分布规律,则上述纯横向易磁化结构模型可以用高斯函数加以修正,此处用理想模型的“台阶状”磁阻抗曲线与高斯分布曲线“卷积”的计算机拟合方法实现,结果如图2所示.
图2(c)的巨磁阻抗比可用下式表示:

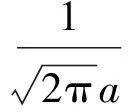
式(1)中:Hex是外加直流磁场值;a代表横向易磁化分量的整齐度;b是与横向易磁化结构对应的巨磁阻抗比值;Hk是横向易磁化结构的各向异性场;“*”是卷积运算符.
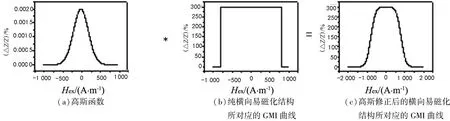
图2 纯横向易磁化结构模型的高斯修正过程
1.1.2 纯纵向易磁化结构模型

图3 理想化学的纯纵向易磁化结构模型及所对应的GMI曲线
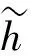

式(2)中:l代表纵向易磁化分量的整齐度;Hk为外加直流磁场值;c是与纵向易磁化结构对应的最大巨磁阻抗比值.
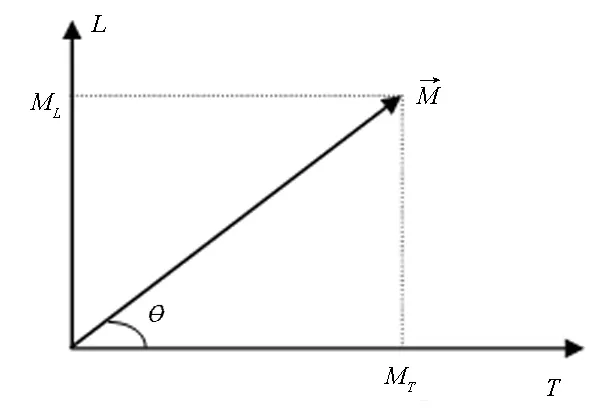
图4 磁结构矢量正交分解图
1.2正交分解法分解实际磁化矢量
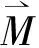
然而,在实际磁性材料中往往存在复合的磁结构,具有不同的易磁化矢量,使得横向易磁化分量和纵向易磁化分量也不同,用单个的横向易磁化结构和纵向易磁化结构组合往往与实际磁结构不够吻合.为此,需要取多个横向易磁化矢量分量和纵向易磁化矢量分量所对应的GMI曲线进行叠加,即:将式(1)中的A,B取不同值A1,A2,A3,…,An和B1,B2,B3,…,Bn,可得T1,T2,T3,…,Tn;式(2)中取不同的c,l值可得L1,L2,L3,…,Ln,然后进行叠加,得
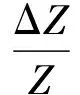
在GMI实验曲线的计算机拟合过程中,横向易磁化分量所对应的GMI曲线取前2项,纵向易磁化分量所对应的GMI曲线取前1项叠加即可获得比较理想的效果,即式(3)可简化为
2 GMI曲线的计算机拟合
按式(4)进行GMI曲线拟合,其中:
T1,T2分别代表横向易磁化分量1和横向易磁化分量2所对应的GMI曲线;L1表示纵向易磁化结构所对应的GMI曲线;a1,a2分别代表横向易磁化分量1和横向易磁化分量2的整齐度,b1,b2分别代表横向易磁化分量1和横向易磁化分量2对应的巨磁阻抗比值,Hk1,Hk2分别代表横向易磁化分量1和横向易磁化分量2的各向异性场;c代表纵向易磁化结构对应的巨磁阻抗比值,l代表纵向易磁化结构的整齐度;Hex是外加直流磁场值,“*”是卷积运算符.
通过对式(4)相关各特征参量的调整,可得到不同形状的GMI曲线.对特征参量a1的调整,可得如图5所示的拟合GMI曲线及解叠子谱图.
定义:T1面积分与F面积分的比值P1对应于横向易磁化分量1所占比例,T2面积分与F面积分的比值P2对应于横向易磁化分量2所占比例,L1面积分与F面积分的比值PL对应于纵向易磁化结构所占比例.通过计算机拟合,可得如图5所示的拟合GMI曲线解叠子谱图的各特征参量值,具体见表1.
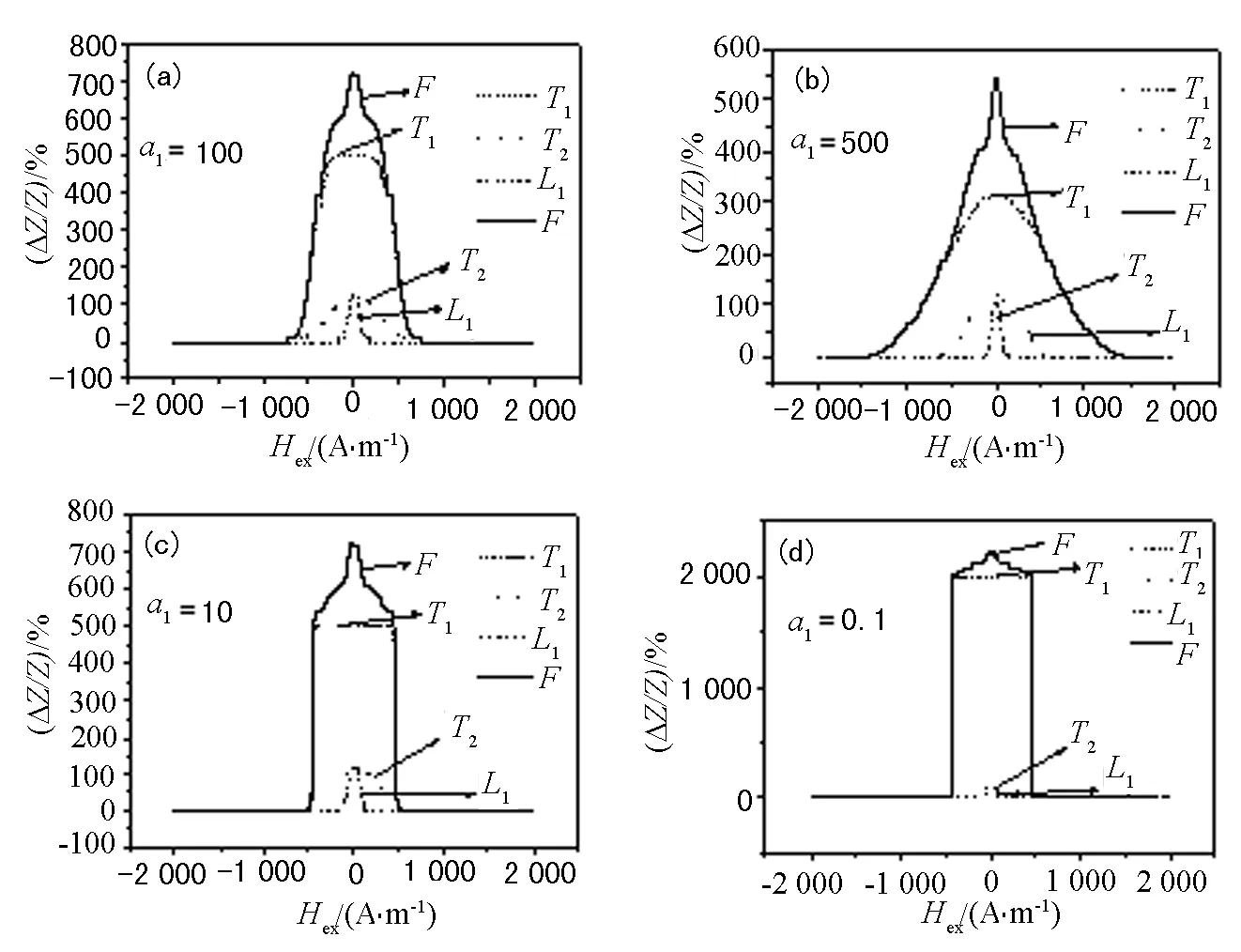
图5 a1取不同值时的拟合GMI曲线

表1 图5中拟合GMI曲线解叠子谱图的各特征参量值
通过对各向异性场Hk1的调整,可得如图6所示的拟合GMI曲线及解叠子谱图.

图6 Hk1取不同值时的拟合GMI曲线
通过对横向易磁化分量2的整齐度a2的调整,可得如图7所示的拟合GMI曲线及解叠子谱图;通过对横向易磁化分量2的各向异性场Hk2的调整,可得如图8所示的拟合GMI曲线及解叠子谱图.

图7 a2取不同值时的拟合GMI曲线
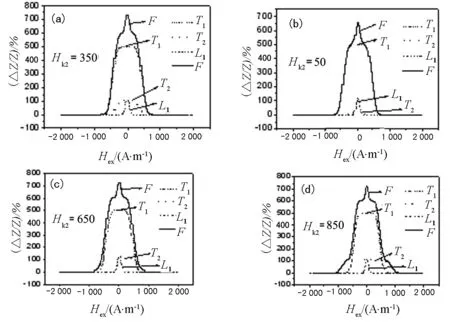
图8 Hk2取不同值时的拟合GMI曲线
通过对纵向易磁化结构对应的巨磁阻抗比值c的调整,可得如图9所示的拟合GMI曲线及解叠子谱图;通过对纵向易磁化结构的整齐度l的调整,可得如图10所示的拟合GMI曲线及解叠子谱图.
3 GMI实验曲线的磁结构分析
根据以上GMI曲线拟合方法可以对各种实验GMI曲线进行拟合,并根据拟合所得解叠子谱特征参量获得材料内部磁结构信息.图11为FeCo合金薄带在300 kHz,32 A/mm2直流电退火的纵向驱动的实验GMI曲线,图12(a)是按上述方法进行拟合所得曲线和实验曲线的对比图,图12(b)是拟合所得各解叠子谱,其特征参量列于表2.
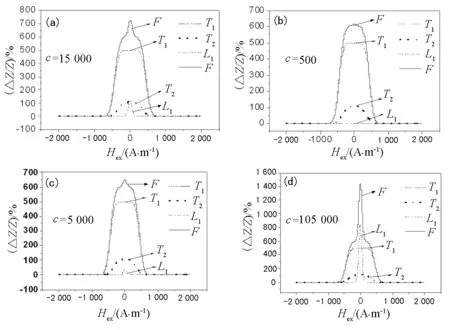
图9 c取不同值时的拟合GMI曲线

图10 l取不同值时的拟合GMI曲线
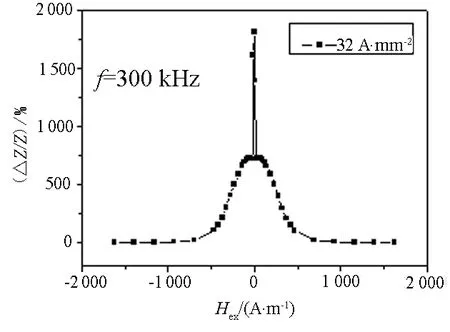
图11 FeCo合金薄带实验GMI曲线

图12 实验GMI曲线拟合效果图

表2 图12(b)GMI拟合曲线解叠子的各种特征参量值
由表2可知,实验样品具有复合磁结构,横向磁结构分量1的各向异性场为280 A/m,占总磁结构的55%,整齐度为98;横向磁结构分量2的各向异性场为150 A/m,占总磁结构的38.26%,整齐度为350;纵向磁结构分量占总磁结构的6.74%,整齐度为13.
由于测量磁性材料的纵向驱动巨磁阻抗效应曲线无需对材料进行任何处理,因此,采用本方法进行磁结构分析具有明显的简便易行的优势.
4 结 论
从简单的纯横向和纯纵向易磁化结构与GMI曲线对应的模型出发,结合磁化矢量的正交分解手段,通过拟合可以获得各种拟合GMI曲线;利用这种GMI曲线拟合方法,能够对实验GMI曲线进行拟合,并从拟合所得解叠子谱特征参量获得被测量磁性材料的横向各向异性场、纵向易磁化结构与横向易磁化结构比例、纵向易磁化结构及横向易磁化结构的整齐度等内部磁结构信息.
[1]Bitter F.On Inhomogeneities in the Magnetization of Ferromagnetic Materials[J].Phys Rev,1931,38:1903-1905.
[2]Nobuo S,Hideo F,Yutaka S.A New Type of Magnetic Domain Structure in Negative Magnetostriction Ni-Fe Films[J].J Phys Soc Japan,1964,19(7):1116-1125.
[3]单凤兰,李吉学.用纵向克尔磁光效应观察磁畴[J].物理实验,1990,10(4):159-160.
[4]Wolfgang R,Rudolf S,Alex H.Quantitative observation of magnetic domains with the magneto-optical Kerr effect[J].J Magn Magn Mater,1987,68:7-14.
[5]Löhndorf M,Wades A,van den Berg H A M,et al.Structure of cross-tie wall in thin Co films resolved by magnetic force microscopy[J].Appl Phys Lett,1996,68(25):3635-3637.
[6] García J M,Asenjo A,García D,et al.Properties of amorphous magnetic materials by magnetic force microscopy[J].J Non-cryst Solids,2001,287:55-59.
[7]CoÏsson M,Celegato F,Olivetti E,et al.Stripe domains and spin reorientation transition in Fe78B13Si9thin films produced by rf sputtering[J].J Appl Phys,2008,104:033902.
[8]白春礼.扫描隧道显微术及其应用[M].上海:上海科学技术出版社,1992:541.
[9]Mohri K,Kohsawa T,Kawashima K,et al.Magneto-inductive Effect (MI effect) in Amorphous Wires[J].IEEE Trans Magn,1992,28(5):3150-3152.
[10]Herzer G.Magnetic field induced anisotropy in nanocrystalline Fe-Cu-Nb-Si-B alloys[J].Mater Sci Eng A,1994,181/182:876-879.
[11]Herzer G.Creep induced magnetic anisotropy in nanocrystalline Fe-Cu-Nb-Si-B alloys[J].IEEE Trans Magn,1994,30(6):4800-4802.
[12]Hofmann B,Kronmüller H.Creep induced magnetic anisotropy in nanocrytalline Fe73.5Cu1Nb3Si13.5B9[J].Nanostructured Mater,1995,6:961-964.
[13]Hofmann B,Kronmüller H.Stress-induced magnetic anisotropy in nanocrystalline FeCuNbSiB alloy[J].J Magn Magn Mater,1996,152(1/2):91-98.
[14]Fang Yunzhang,Zheng Jinju,Wu Fengmin,et al.Mesostructural origin of stress-induced magnetic anisotropy in Fe-based nanocrystalline ribbons[J].Appl Phys Lett,2010,96:092508.
[15]Man Qikui,Fang Yunzhang,Sun Huajun.Fangmin,et al.A new type of longitudinally driven GMI effect of FeCo-based alloy[J].Chin Sci Bull,2008,53(3):329-334.
[16]Phan M H,Peng Huaxin.Giant magnetoimpedance materials:Fundamentals and applications[J].Prog Mate Sci,2008,53:323-420.
AmodelforcharacterizationonthemagneticstructureinmagneticmaterialswithGiantMagneto-impedanceeffect
FANG Yunzhang, FAN Xiaozhen
(CollegeofMathematics,PhysicsandInformationEngineering,ZhejiangNormalUniversity,JinhuaZhejiang321004,China)
A model for characterization on the magnetic structure in magnetic materials with Giant Magneto-impedance effect was investigated. A relation model for the dependence of giant magneto-impedance effect on simplified magnetic structure was proposed. A various of Magneto-impedance effect profiles were obtained by means of adjusting the characteristic parameters of the relation model combined with the method for orthogonal decomposition of the magnetized vector. The composition and characteristics of internal magnetic structure in the magnetic materials could be obtained by analyzing the characteristics in the unfolding sub-spectrum. These results showed important for the aim to develop new methods for characterization of magnetic structure in magnetic materials, to control the internal magnetic structure and improve the magnetic properties for developing new magnetic materials.
magnetic structure; Giant Magneto-impedance effect; magnetization vector; simulation; dodel.
1001-5051(2011)01-0001-08
O482.5
A
2010-11-15
国家自然科学基金资助项目(50871104;11079029);科技部资助项目(2009GJC20019);浙江省自然科学基金资助项目(Y4080324)
方允樟(1963-),男,浙江金华人,教授.研究方向:磁性功能材料.
(责任编辑 杜利民)

