基于蒙特卡罗模拟的岩石点载荷试验数据处理*
尚振华,徐必根
(长沙矿山研究院金属矿山安全技术国家重点实验室,湖南长沙410012)
基于蒙特卡罗模拟的岩石点载荷试验数据处理*
尚振华,徐必根
(长沙矿山研究院金属矿山安全技术国家重点实验室,湖南长沙410012)
结合某铁矿采空区研究的岩石力学试验,以蒙特卡罗模拟处理点荷载试验结果,利用概率论与统计理论,结合Excel插件@Risk对岩石点载荷强度指标进行分析及最终取值。该方法采用计算机多次模拟,较传统的处理方式易分析、易理解,同时提高了点载荷强度的精度与可信度,另外受问题条件限制的影响较小,可很好的提高可行性。
岩石强度;点载荷试验;试验数据;蒙特卡罗;概率分布;@Risk
点荷载试验由于具有现场操作简单、取样要求不高和试验周期短等特点,在岩土工程中得到越来越多的应用[1]。一般情况下,试验数据按传统方式处理后将其结果作为准确值的一个估计,但该估计值与实际值之间将会产生一个估计误差,而这个误差将会或多或少地带来一定的损失[2]。另外,在试验过程中,由于试验条件的限制使得操作无法严格按照设计执行,以致一些外部因素使试验结果出现了随机性,此外,岩体的空间变异性和不同的隶属关系使得工程岩组的分类具有了不确定性。
1 传统方式的数据处理
在现实中,一方面,并不能保证试验过程完全按照期望的要求进行,另一方面,过于保守或者过于乐观的估计结果所包含的错误综合在一起,常常会导致所得结果与真实结果有很大差异,于是根据该“预期”方式做出的试验值可能是错误的。
传统试验结果处理方法是通过综合分析模型变量的单“点”估计来预测一种结果,采用标准Excel电子表格进行简单的整理、计算,但是该计算的变量只能估计,因为无法确切得知实际将产生的值。
某铁矿采空区研究中要进行岩石力学实验,但由于该铁矿围岩之一花岗斑岩风化较为严重,较难取得完整的岩芯试样,于是在该矿+130m中段、+100m中段和+70m中段分别采集了部分试样,在长沙矿山研究院岩石力学实验室利用A125型携带式点载荷仪进行点载荷强度试验,按照传统的ISRM法及回归分析计算得出花岗斑岩的点载荷强度指标Is(50)=2.70,抗压强度σc=64.80MPa。
2 蒙特卡罗分析的基本原理
蒙特卡罗(MonteCarlo)方法,又称计算机随机模拟方法,是一种基于“随机数”的计算方法。这一方法源于美国在第二次世界大战研制原子弹的“曼哈顿计划”,该计划的主持人之一数学家冯·诺伊曼用驰名世界的赌城——摩纳哥的MonteCarlo来命名这种方法[3]。
它是用一系列随机数来近似解决问题的一种方法,是通过寻找一个概率统计的相似体并用试验取样过程来获得该相似体的近似解的处理数学问题的一种手段。运用该近似方法所获得的问题的解更接近于试验结果,而不是经典数值计算结果。
它的基本思想是为了求解数学、物理、工程技术以及生产管理等方面的问题,首先建立一个概率模型或随机过程,使它的参数等于问题的解;然后通过对模型或过程的观察或抽样试验来计算所求参数的统计特征;最后给出所求解的近似值,而求解的确定精确度可用估计值的标准误差来表示[4]。
假设所要求的量x是随机变量ε的数学期望E(ε),那么近似确定x的方法是对ε进行N次重复抽样,产生相互独立的ε值的序列ε1、ε2、…、εn,并计算其算术平均值:

根据柯尔莫哥罗夫(Komogorov)的加强大数定律有:

3 基于蒙特卡罗模拟的数据处理
3.1 试验数据的分布拟合
Excel插件@Risk采用蒙特卡罗模拟,对采集到的试验数据(岩心直径的平方、试样破坏时的总荷载P)应用MicrosoftExcel的插件@Risk进行分布拟合,利用蒙特卡罗抽样得出二者分别基本符合三角分布(Triangledistribution)和威布尔分布(Weibull distribution),见图1、图2。
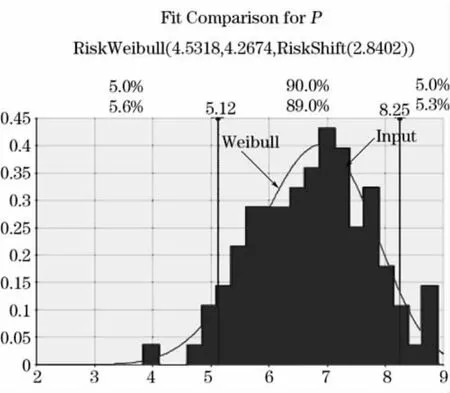
图1 岩心直径的平方的分布拟合
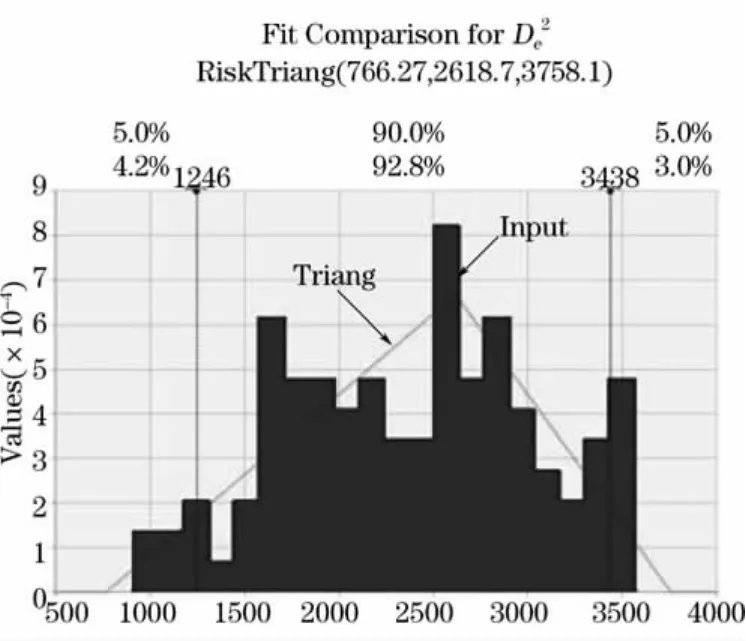
图2 试样破坏时的总荷载P的分布拟合
同样,对整理的数据(标准点载荷强度Is(50)、抗压强度σc)应用相同方法得出二者均基本符合正态分布(Normaldistribution),见图3、图4。
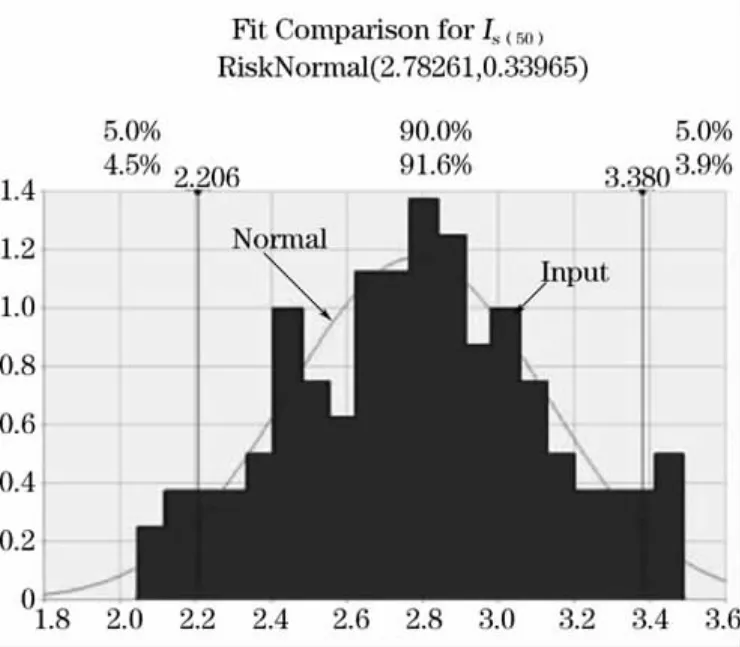
图3 标准点载荷强度Is(50)的分布拟合

图4 抗压强度σc的分布拟合
3.2 数学模型的建立
(1)定义输入变量及相关。将分布拟合得出的花岗斑岩的各个统计量(、P、Is(50)、σc)分别写入Excel不同的单元格,即对这些统计量的不确定值指定概率分布函数,该分布包含了每个参数的具体情况,如Is(50)服从正态分布RiskNormal(2.78261,0.33965)。利用传统的Excel功能对和P进行数值拟合,得出二者相关系数为0.89。然后通过@Risk的“定义相关”功能,以散点矩阵的方式输入并以散点图的方式显示二者之间的相关性。
(2)定义输出变量。利用@Risk的分布函数RiskOutput()输出重点关注的点载荷的强度指标Is(50)和σc。其中,Is(50)的输出为RiskOutput("Is(50)(MPa)")+的输出为RiskOutput("σc(MPa)")+24×Is(50)。这里添加的RiskOutput函数中的“+”,表示为根据输出函数需要来选择合适的单元格作为模拟输出,并将输出分别命名为“Is(50)(MPa)”和“σc(MPa)”。
3.3 模拟计算及结果分析
该模型利用@Risk对采集到的试验数据应用基于最优化的蒙特卡罗法进行分析处理,并在Excel中以概率分布的形式用图形显示可能的多种结果及其概率,这允许在存在不确定因素的情况下做出最好的点载荷试验处理结果。
此次点载荷试验的数据处理结果在蒙特卡罗模拟的基础上执行5个循环,每个循环迭代1000次,计算结果见图5,计算结果的分布拟合见图6。
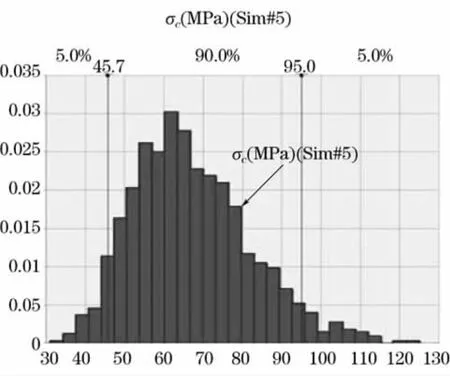
图5 σc的蒙特卡罗模拟结果
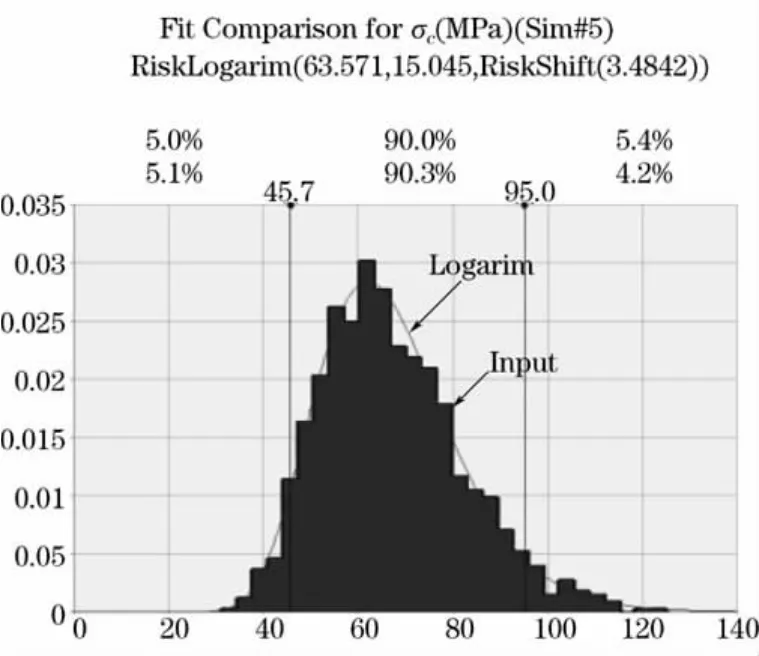
图6 σc模拟结果的分布拟合
该计算结果基本符合对数正态分布(Logarithmicnormaldistribution)。假设给定显著性水平n=0.05,即置信水平为95%时,由蒙特卡罗方法得出的置信区间为[45.7,95.0],最终σc的取值为期望值67.60MPa。较传统方式处理结果提高了2.80 MPa,约4.32%,也进一步验证了传统的“点”估计在该次试验结果的处理过程中略偏保守。
通过绘制“龙卷风”图(见图7),很直观地得出对σc的取值影响较大的参数系数分别为Is和,影响系数分别为0.9和0.3,其中π。这也进一步验证了点载荷试验中岩石试样的形状对最终的试验结果有较大的影响。
运用@Risk对所取得的试验数据进行多种组合的模拟计算,得到的模拟结果一方面提高了试验数据处理的精度,另一方面可以以更直观的角度显示多种试验组合带来的不同结果。在该模拟中通过对模拟结果的查看,至少可以得到1000组试验数据及组合,这对进一步了解和分析岩石点载荷试验过程中的各个环境变量对其最终结果的取值有一定的帮助。

图7 对σc回归分析的“龙卷风”
4 结论
点载荷试验是岩体工程中岩体分级(RMR,CSMR等)研究和强度参数的一个十分重要的指标,但由于传统方法以“点”估计的方法对试验结果处理,常常导致实际情况的结果与估计的结果有很大差异。借助@Risk基于蒙特卡罗法对后期试验数据分析处理,并针对现实情况中存在的不确定因素加以组合、模拟,能以更加直观、准确的方式显示所有可能“预期”的结果。
@Risk基于蒙特卡罗模拟以概率统计理论为基础,以随机抽样(随机变量的抽样)为手段,在很多方面有重要的应用。它在岩石点载荷试验数据处理方面的优点表现在3个方面:方法和程序的结构简单,易分析、易理解;收敛的概率性和收敛速度与问题的维数无关,很好地避免了维数问题;受问题条件限制的影响较小,很好地提高可行性。
[1]李茂兰,钟光宙.岩石点荷载试验及其应用[M].西安:西安交通大学出版社,1994.
[2]谭文辉,乔兰,李治平.岩石点荷载强度指标取值的模糊随机方法[J].金属矿山,2001,(10).
[3]王坤.MonteCarlo方法及其简单应用[J].科技信息,2010,(14).
[4]徐钟济.蒙特卡罗方法[M].上海:上海科学技术出版社,1985:5-6.
863计划重点课题(2008AA062104).
2011-09-08)
尚振华(1985-),男,河南安阳人,硕士研究生,主要从事矿山岩石力学及地压监控技术研究,Email:szh207@gmail.com。

