基于四面体的不规则表面文物体积计算

张小青，朱 光，2，侯妙乐，黄 鹤，2

(1.北京建筑工程学院测绘与城市空间信息学院，北京100044;2.现代城市测绘国家测绘地理信息局国家重点实验室，北京100044)

基于四面体的不规则表面文物体积计算

张小青1，朱 光1，2，侯妙乐1，黄 鹤1，2

(1.北京建筑工程学院测绘与城市空间信息学院，北京100044;2.现代城市测绘国家测绘地理信息局国家重点实验室，北京100044)

鉴于不规则表面的文物很难直接进行体积测量，提出一种从三角格网模型计算不规则表面文物体积的方法。该方法利用高精度三维激光扫描仪对复杂表面文物进行扫描获取三维点云数据，并通过对三维点云数据的处理和拓扑重建得到文物的三角格网模型，引入四面体的有向体积法，通过求四面体有向体积来计算文物三维模型的体积。同时，分析此类算法的误差，并在VC# 2008环境下利用OpenGL对该三维模型进行显示。

四面体;三维模型;三角格网;体积计算

一、引 言

随着自然的侵蚀和人类活动的影响，前人留下的珍贵而丰富的文化遗产正在逐渐被损毁、破坏和消失。如何利用先进的技术手段来保护、修复这些宝贵文物，成为迫在眉睫的问题［1］。在文物修复中经常需要估算修复材料的用量，然而一些文物结构非常复杂，表面呈不规则形状，传统测量方法无法直接求得精确体积以估算材料用量。因此，通常采用把体积参数转换成质量和密度的关系而进行间接测量。但间接测量方式易受条件、经验的约束，且测量速度慢、精度低、自动化程度不高［2］。而近年来不断发展和成熟的三维建模技术，却给文物保护工作开创了一个全新的局面。通过三维扫描手段，可将文物的几何、纹理等信息进行数字化，尤其是对不规则表面文物的保护、修复提供了测量保障。

二、研究现状

采用三维激光扫描仪的非接触扫描，可直接获得表征物体表面形状的点云数据，进而测量不规则表面体的体积。针对基于不规则表面体三维点云数据的体积计算方法，周会成等提出一种从三维点云计算活塞腔体积的方法［3］。该方法通过对三维点云的处理，分割出参考平面，重构其曲面几何模型，用数值积分的方法计算活塞腔的体积，但这种方法要求物体表面较规则。刘玉身提出拟蒙特卡罗(Quasi-Monte Carlo)方法计算点模型的体积［4］。该算法虽然克服了重建模型需要消耗大量时间和空间的不足，但判断点云边界时的程序繁琐，不宜处理大规模的数据处理。针对点云生成三角网格模型的体积计算，王泉德提出了一种根据三角网格模型的三角面片集合计算模型体积的方法［5］。该方法通过指定投影平面，计算每个三角面片及其在投影平面上的投影所围成的凸五面体的带符号体积，整个模型的体积为所有凸五面体带符号体积的代数和，但该方法需要判断三角形拓扑关系。戴文俊等提出计算三维实体模型体积的适应性方法［6］。该方法首先用一组等距的平行平面对网格模型进行分层剖分，并利用平面简单多边形的带符号面积公式求取相应截面的面积，然后根据相邻平面间的距离估算模型体积。这种算法可得到任意实体模型近似值和精确值计算方法，但算法中剖分模型的计算花费较大。

本文利用三维激光扫描仪对具有复杂表面的文物进行扫描获取其表面几何信息，将获取的表面点云数据通过拓扑重建得到文物的三角网格模型。针对文物的三角网格模型，提出一种四面体有向体积法来计算三角网格模型体积法，并对算法进行了改进。该算法首先对模型进行仿射变换将模型平移，然后计算三角网格中所有三角形与零向量点所构成的四面体的体积，所有的四面体带符号体积的代数和即为整个模型的体积。

三、基于四面体的网格模型体积计算法

四面体是三维空间最简单的不规则体单元，是进行三维几何拓扑关系描述的最基本元素之一。利用计算四面体有向体积来计算三角网格模型体积的实质是利用三维激光扫描仪对文物进行扫描获取其表面几何信息点云，然后经过对点云数据预处理并通过拓扑重建得到文物的三角网格模型，从而计算出表面复杂的文物的体积。其计算流程包括对文物三维空间数据采集、数据预处理、文物三维模型构建等数据准备部分和基于四面体的模型体积计算部分。

1.数据准备

为获取文物表面高精度三维空间点云数据，本文利用了便携式关节臂测量系统(CIMCORE Infinite 2.0)，其三维空间坐标测量精度为±0.045 mm。由于扫描实体模型的过程中难免会受到环境和载物装置等干扰而出现杂点与噪点，因此需要对数据进行剔除处理，并且要通过精简数据来减少信息处理量，对多视图扫描文件进行拼合处理。通过扫描获得的点云模型实质上是无数个具有三维坐标的离散点形成的表面形态，各个点之间不存在拓扑关系，并没有构成文物的实际表面。本文利用三角格网模型方法来构建三维形体，并以一种标准三维模型文件OBJ格式存储。

对于任一给定的网格模型，只有在它的网格面片围成有限封闭空间的情况下，求其体积才有意义。因此，在计算体积之前应确保模型的每个面片均为三角形，并且三角形的法向量与三角形的3个顶点编号顺序为右手规则，即所有三角形面片的法向一致，均指向体外。本文讨论的网格模型也属于此类模型，且满足以下条件:① 网格上的每个面片都是平面凸多边形;②网格上的每条边由且只由两个面片共有，并且共用网格上任一顶点的各面片在该顶点处形成的曲面与单位圆拓扑同构。

2.基于四面体的模型体积计算

对于构建完成的文物三角格网模型，采用的基于网格模型体积计算方法如下。

设网格模型中的任意一个三角形的3个顶点为A(x1，y1，z1)，B(x2，y2，z2)，C(x3，y3，z3)，如图1所示，则以△ABC为底(按逆时针顺序排列)，以坐标原点O(0，0，0)为顶点的四面体体积为［7］

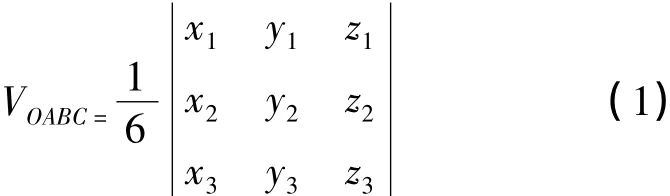
设OA方向的单位向量N，△ABC所在平面一侧的单位法向量为NABC，△ABC按逆时针排列时与N成右手系，则当内积(N，NABC)＞0，四面体体积VOABC为正数，否则为负数。

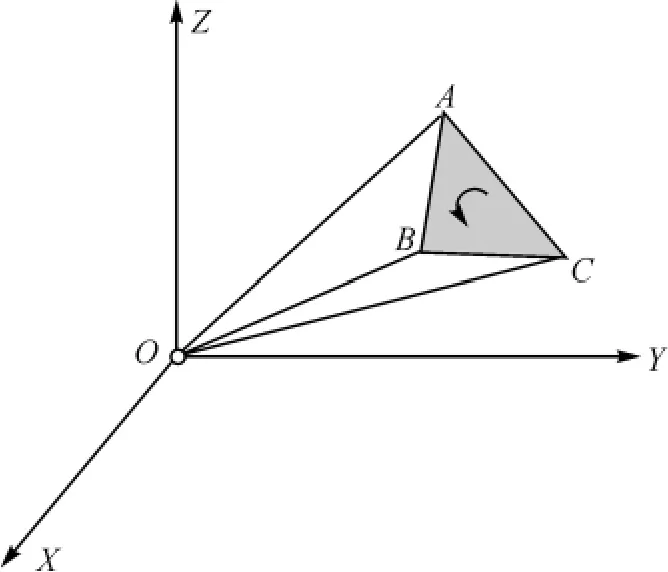
图1 四面体体积计算

如图2所示，设三角格网模型表面由n个分片三角形所组成，外侧面第i个三角形的三个顶点为Ai1(xi1，yi1，zi1)，Bi2(xi2，yi2，zi2)，Ci3(xi3，yi3，zi3)，3个顶点的顺序按曲面外侧逆时针方向排列，则三维模型总体积计算公式为

式中，Vi为第i个三角形与坐标原点构成的带符号体积，其正负符号同样根据原点O和三角形中一顶点构成的向量与三角形的法向量的内积的正负号确定。

图2 三维模型体积计算

由于本文计算的三维模型表面极其复杂且不规则，为了提高体积计算精度，专门对其算法进行了改进。首先在体积计算之前对模型数据进行预处理，将原始三角网模型进行仿射变换，使模型中心平移到坐标原点。然后搜索三角网模型顶点坐标在3个坐标轴方向上的最大值、最小值，分别记为(xmin，xmax)，(ymin，ymax)，(zmin，zmax)，再以点(xmin，ymin，zmin)和点(xmax，ymax，zmax)为对角顶点构成一个包围边界包围整个模型，最后求出模型中心，并在此基础上进行体积计算(如图3所示)。

图3 四面体模型体积计算算法及改进算法

四、试验结果与误差分析

本文以重庆大足石刻千手观音为例(如图4所示)。该千手观音修复中需要贴金箔，而其造型相当复杂，其中准确计算需要修复金箔数量是千手观音修复的关键。本文截取了千手观音的一只手作为试验样品(如图4(a)所示)，构建了其三角格网模型(如图4(c)所示)，并基于上述算法及改进算法进行了计算。计算算法是在VC#2008环境，调用OpenGL函数库编程实现。图5表示针对千手观音单只手计算出的体积，四面体模型体积算法结果为5 681.594 cm3(M1);四面体模型体积计算的改进算法结果为5 683.660 cm3(M2)。将两种算法得到的结果和该只手的体积理论值比较，改进算法能提高0.4%的精度。

图4 千手观音部分数据体积计算实例

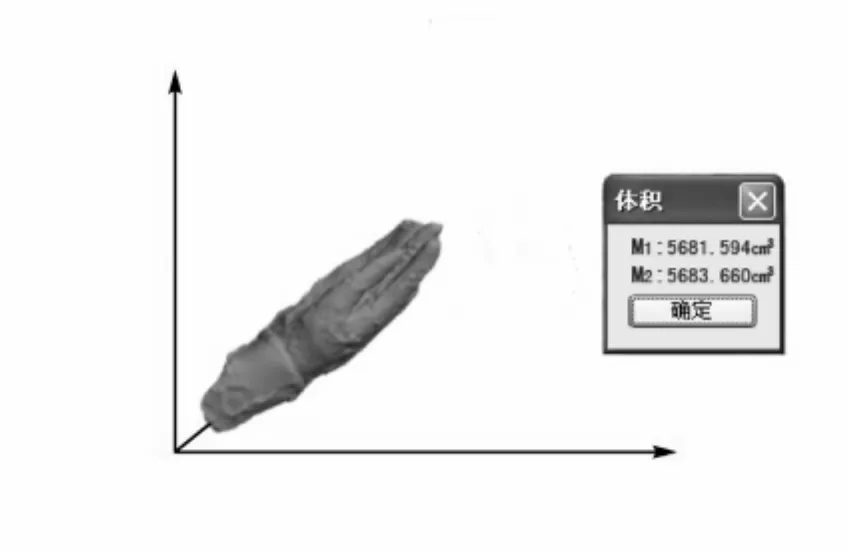
图5 四面体模型体积算法及改进算法的计算结果

通过对此试验数据计算的整个过程可见，影响模型体积计算精度的因素主要有两个方面:①三维点云获取过程。在三维点云数据的获取过程中，扫描仪扫描的点云的密度大小直接影响其精度的离散性，而扫描仪本身的误差与环境因素，也影响实际获得点云数据的精度，因此数据准备过程中的预处理非常必要。②数据建模误差，其体积计算精度与三角格网模型构建数量、精度有关。

五、结束语

本文提出基于三维激光扫描仪获得复杂表面文物三维点云数据，并通过三角格网模型的四面体体积计算算法及改进算法计算其体积的方法。此方法可有效提高复杂表面目标物的体积计算精度，并可利用OpenGL实现简易、高效的模型可视化，可广泛利用于复杂表面文物的体积、面积等计算。

［1］ 张瑞，骆岩林，周明全，等.文物数字化的关键技术［J］.北京师范大学学报:自然科学版，2007，43 (2):150-153.

［2］ 刘震.逆向工程对不规则表面物体的体积测量［J］.计算机技术应用，2009(3):19-20.

［3］ 周会成，陈吉红，黄生华，等.用三维点云计算活塞腔的体积［J］.现代测量与实验室管理，2003(2):16-17.

［4］ 刘玉身.离散模型光滑算法的研究［D］.北京:清华大学，2006.

［5］ 王泉德.任意三角网格模型体积的快速精确计算方法［J］.计算机工程与应用，2009，45(18):32-35.

［6］ 戴文俊，庞明勇，武港山，等.一种任意三维实体网格模型的体积特征提取算法［J］.计算机科学，2006，33(4):198-201.

［7］ ZHANG Cha，CHEN Tsuhan.Efficient Feature Extraction for 2d/3d Objects in Mesh Representation［C］∥ICIP2001.Greece:Thessaloniki，2001:935-938.

Volume Calculation of Surface Irregular Cultural Relic Based on Tetrahedron

ZHANG Xiaoqing，ZHU Guang，HOU Miaole，HUANG He

0494-0911(2011)10-0050-03

P258

B

2011-05-05

张小青(1980—)，女，江西抚州人，硕士生，主要研究方向为精密工程测量。