Newton-Leipnik系统混沌控制

李贤丽， 秦显荣， 王 升， 张秀龙， 严晓波

( 东北石油大学 电子科学学院，黑龙江 大庆 163318 )

0 引言

自1963年Lorenz在确定性系统中发现混沌运动以来，混沌及相关问题研究取得许多进展.由于混沌现象普遍存在于复杂的非线性系统中，混沌控制是混沌应用的关键技术，已经成为非线性科学的重要研究领域.自1990年Ott E等提出OGY方法[1]实现混沌控制以来，许多控制方法，如周期激励法[2]、参数周期扰动法[3]、自适应控制法[4]、线性反馈法等均可实现混沌控制，并在许多领域中得到应用.

混沌控制方法可以分为反馈控制和无反馈控制[5].反馈控制方法可以根据受控系统的状态进行调节，具有微扰较小的优点，但需要预先了解系统的运动状态.实际的非线性系统常常无法预先了解系统的动力学特性.无反馈控制方法不必预先了解系统的状态变量，在实际控制中简单易行，因而在许多领域得到应用.无反馈控制方法多应用于非自治系统的混沌控制，对于自治系统的控制研究较少.李贤丽等[6-8]采用参数周期扰动、周期激励、周期脉冲等无反馈控制方法，对自治系统，如CHAY模型、Rossler系统、Lorenz超混沌系统等进行研究，得到较好的控制结果.

Leipnik R B等在研究具有线性反馈的刚体运动模型时，提出具有双吸引子的Newton-Leipnik混沌系统[9]，该系统在初始条件不同时，存在2个不同的吸引子，因而系统动力学性质更为复杂[10-12].笔者采用周期激励法和参数扰动控制法对Newton-Leipnik双吸引子系统的混沌进行控制，以实现有效控制，并对不同初始条件混沌控制的影响进行比较.

1 Newton-Leipnik系统的动力学性质

1.1 动力学性质

具有双吸引子的Newton-Leipnik混沌系统，为三维非线性自治系统，方程为

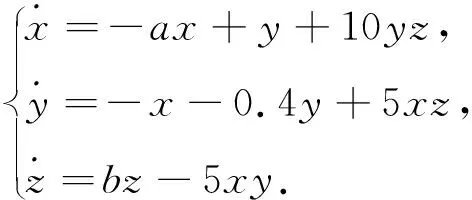
(1)

式中：a，b为参数.

当a=0.4，b=0.175时，系统的初始状态取(0.349,0,-0.160)T和(0.349,0,-0.180)T时，系统的相轨迹见图1.由图1可以看出，系统存在着上、下2个不同的奇怪吸引子，因而Newton-Leipnik系统的动力学行为相对其他单奇怪吸引子系统更为复杂，对初始条件具有较强的敏感依赖性.

对式(1)求解，得到系统具有5个不稳定平衡态分别为(0,0,0)T，(0.239 0,0.030 8,0.210 3)T，(-0.239 0,-0.030 8,0.210 3)T，(0.031 5,-0.122 4,-0.110 3)T，(-0.031 5,0.122 4,-0.110 3)T，其中：第2、3个平衡态处于上吸引子的中心，第4、5个平衡态处于下吸引子的中心.根据线性稳定性分析，对第1个平衡态，在平衡点邻域将方程线性化，得到3个特征值：

λ1=0.175 0,λ2=-0.4+i,λ3=-0.4-i.

对第2、3个平衡态，得到3个特征值：

λ1=-0.799 8,λ2=0.087 4+1.211 5i,λ3=0.087 4-1.211 5i.

对第4、5个平衡态，得到3个特征值：

λ1=-0.799 5,λ2=0.087 3+0.875 2i,λ3=0.087 3-0.875 2i.

因而这5个平衡态为不稳定焦结点.系统的初始条件决定系统相轨迹的运动趋势，最后形成双吸引子的复杂结构.当a变化时，在平衡态(0,0,0)T处，系统的线性化方程的特征值为

当a=-0.4时，系统从不稳定态经hopf分岔转变为稳定的极限环型振荡，即非线性周期运动.

1.2 数值计算

采用四阶龙格—库塔法，对非线性微分方程式(1)求数值解，得到xmax随参数a变化分岔结构图(见图2)，其中：横坐标为a，纵坐标为x的极大值，可以观察到明显的倍周期分岔通向混沌的过程，当a=0.36时，系统为2周期运动；当a=0.368时，系统为4周期运动.z随t变化的时序图见图3和图4.

图1 系统的奇怪吸引子

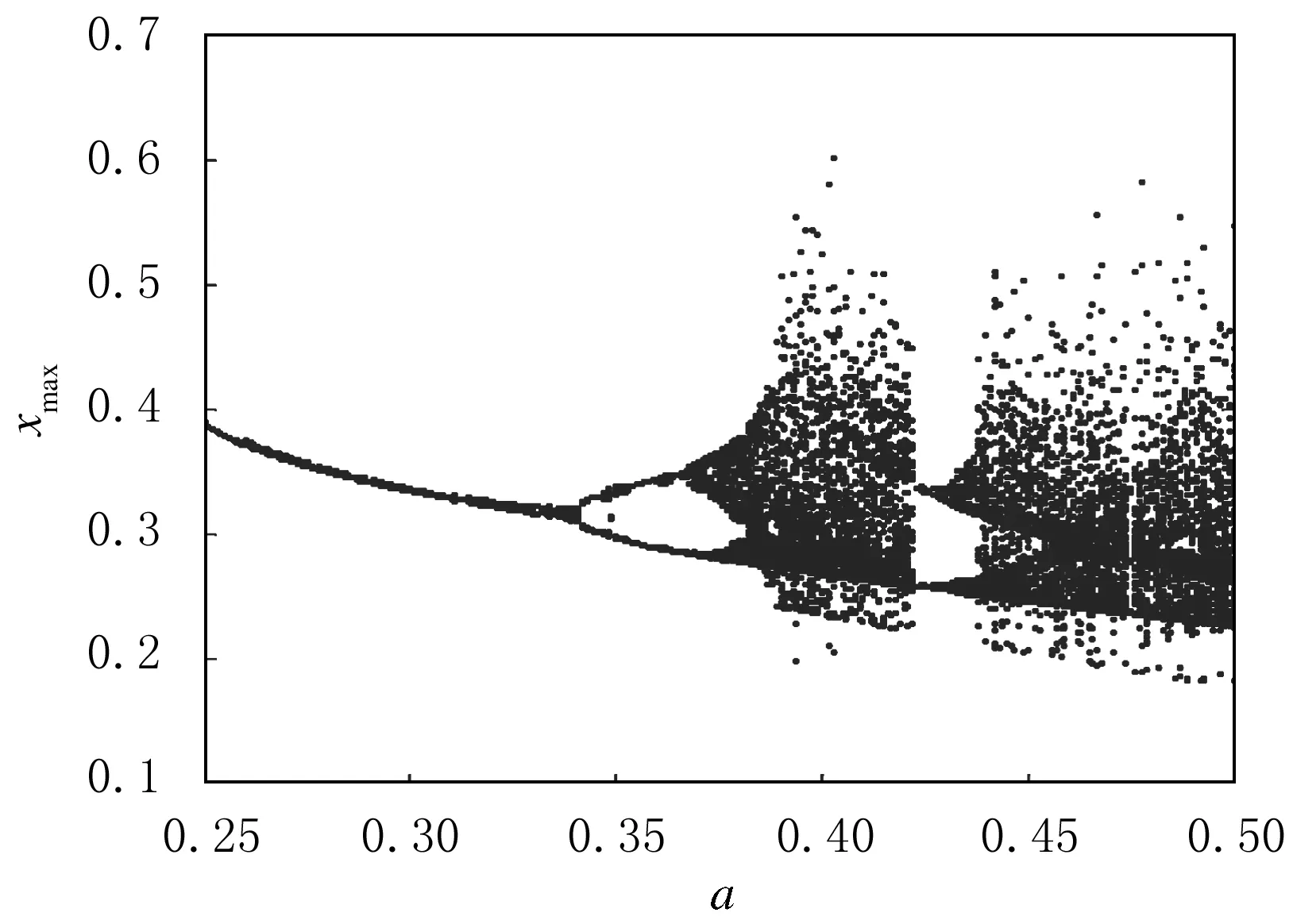
图2 系统随a变化的分岔图

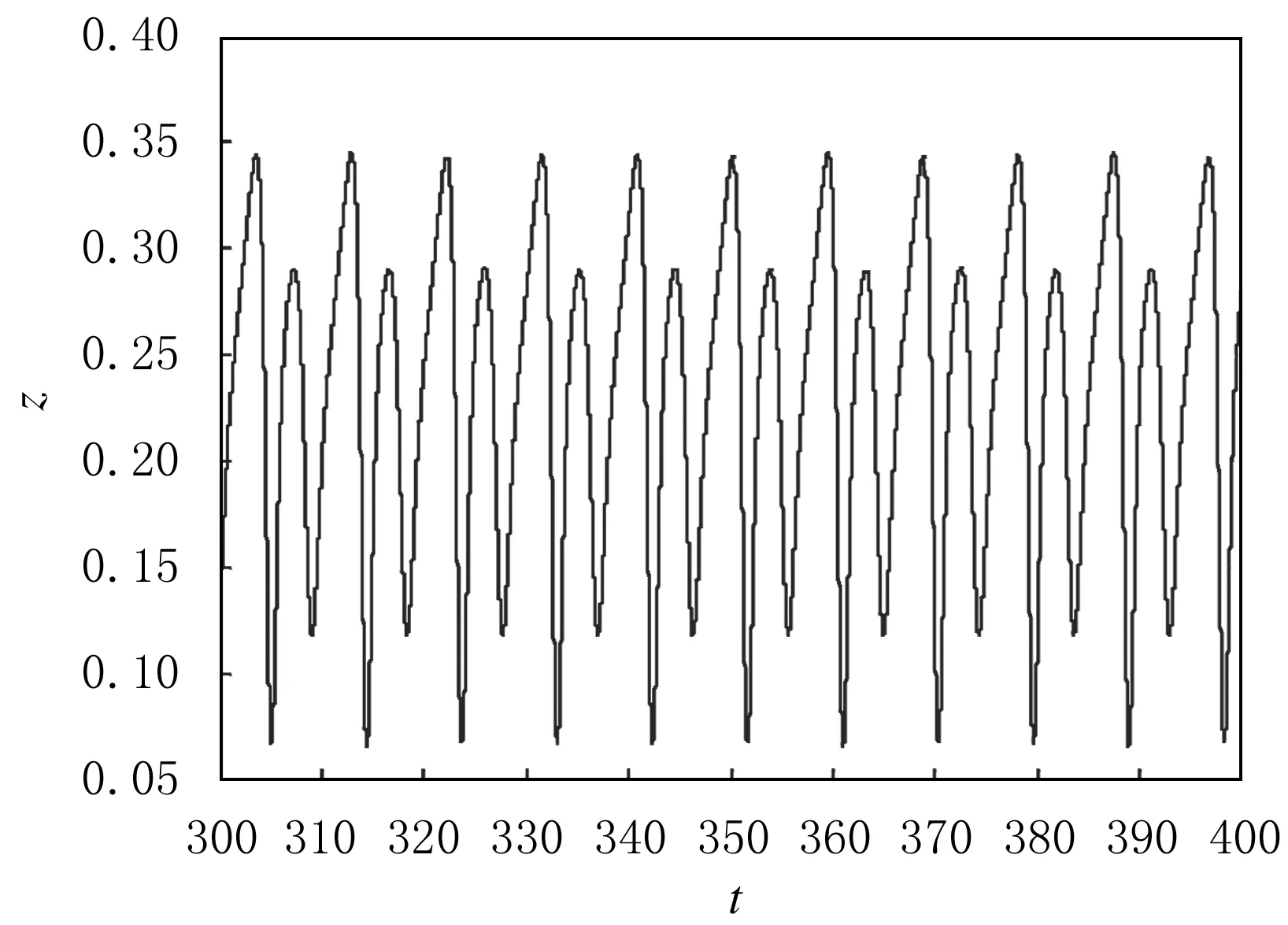
图3 系统的2周期时序图

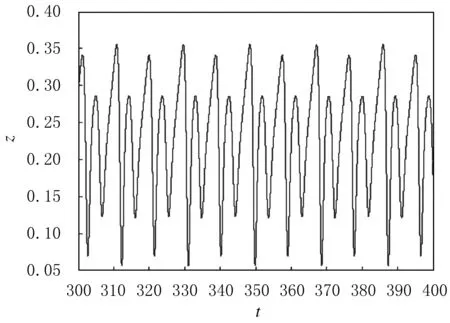
图4 系统的4周期时序图

2 混沌控制计算

在Newton-Leipnik系统中，取a=0.4，b=0.175时混沌运动状态，选取初始条件为(0.349,0,-0.160)T作研究.采用周期激励和参数周期扰动控制方法对Newton-Leipnik系统的混沌运动进行控制，它们根据混沌运动对初始条件的高度敏感性和混沌轨道中镶嵌着无穷多个不稳定的周期轨道性质，利用共振原理和混沌轨道的遍历性对系统的混沌运动进行抑制.

2.1 周期激励控制

周期激励法是通过给系统加入附加的周期强迫力的方法，控制动力学体系的混沌运动状态.在方程(1)右侧加入周期激励项F：

F=rcosωt,

(2)

式中：r为周期激励振幅；ω为激励频率.该方法可调参数为r和ω，通过适当调节它们实现混沌运动控制.

在系统方程(1)的第1式的右侧加入周期性外力式(2)，方程为

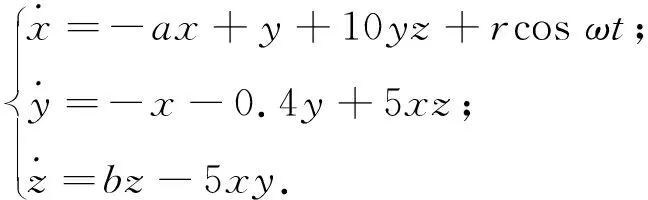
(3)

计算结果表明，当ω=3.2时，对控制参数r循环运算，得到控制结果随激励振幅r变化的结果见图5(a)；当0.30≤r≤0.42时，能够将混沌运动控制为规则周期运动，r=0.4时的系统三维相图见图5(b).

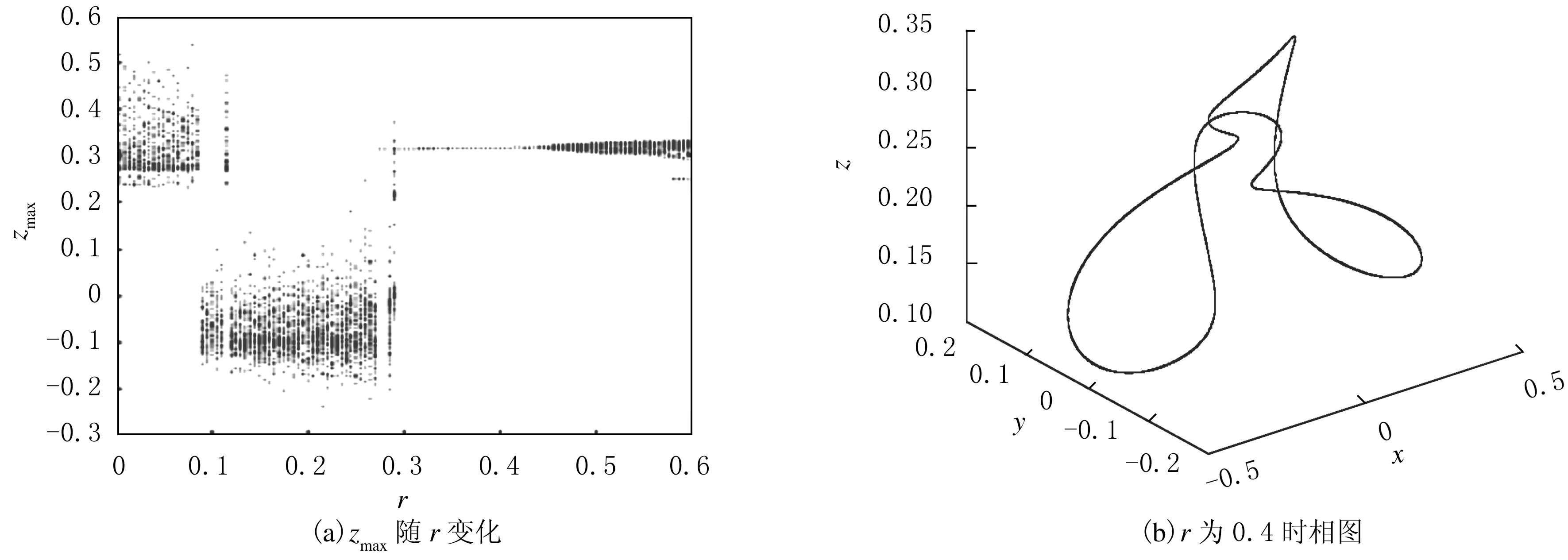
图5 ω为3.2时的周期激励控制

将式(2)加在系统方程(1)的第3式中，进行周期激励控制.当ω=2.0时，得到控制结果随激励振幅r的变化(见图6(a)).由图6(a)可以看出：当0.14≤r≤0.3时，系统被控制为1周期运动.当r=0.2时，系统相图见图6(b).

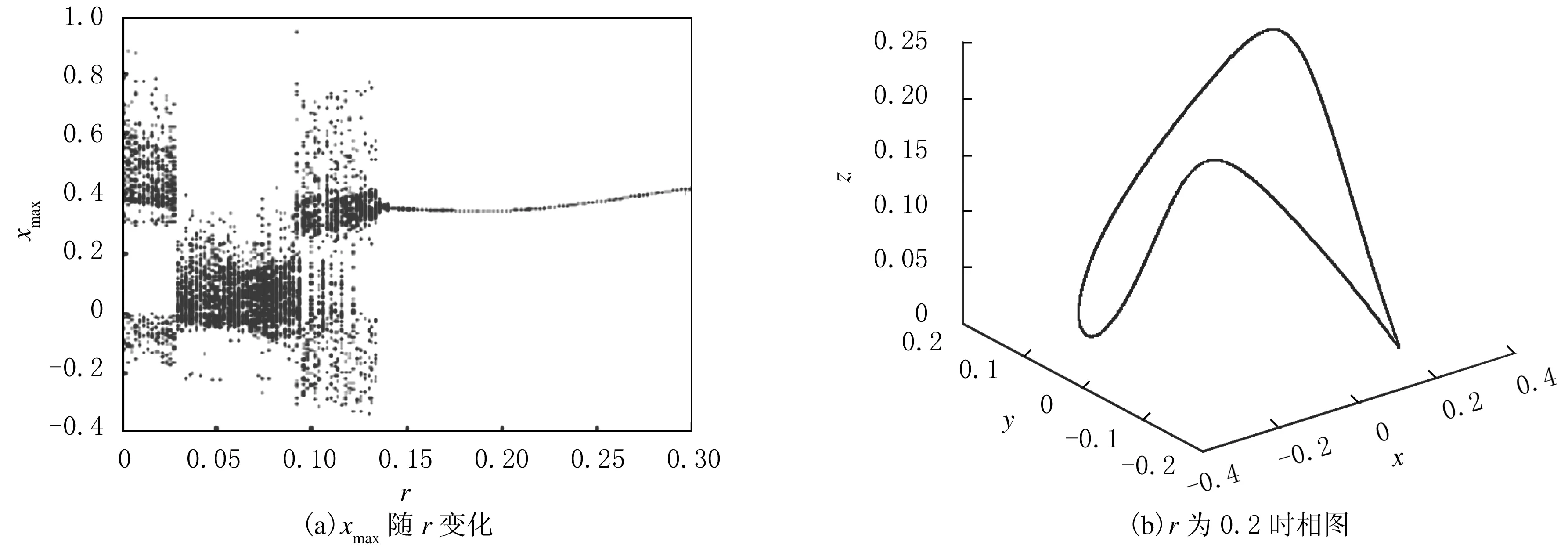
图6 ω为2.0时的周期激励控制

对系统方程第1和3式进行控制，均可实现控制.将控制后得到的周期态与原系统的周期态进行比较，控制得到稳定的周期轨道并不是原系统的周期轨道，系统的性质发生变化，产生新的动力学行为.

2.2 参数周期扰动控制

在系统方程中，选取a作为控制参数，对其进行周期扰动，即把式(1)的a改为

a′=(1+rcosωt)a,

(4)

式中：r为参数周期扰动的幅值；ω为参数周期扰动频率.可以通过调节的控制参数r和ω，将系统的混沌态抑制为规则的周期运动，从而实现混沌控制.

将式(4)代入系统方程(1)中，则方程(1)的形式为

(5)

调节控制参数r和ω：当T=7.3时，改变控制幅值r得到稳定控制，当0.78≤r≤1.2时，除个别值外，系统能够被稳定控制成1周期运动，系统受参数周期扰动后，得到控制结果随r的变化(见图7(a))；当r=0.8时，系统相图见图7(b).

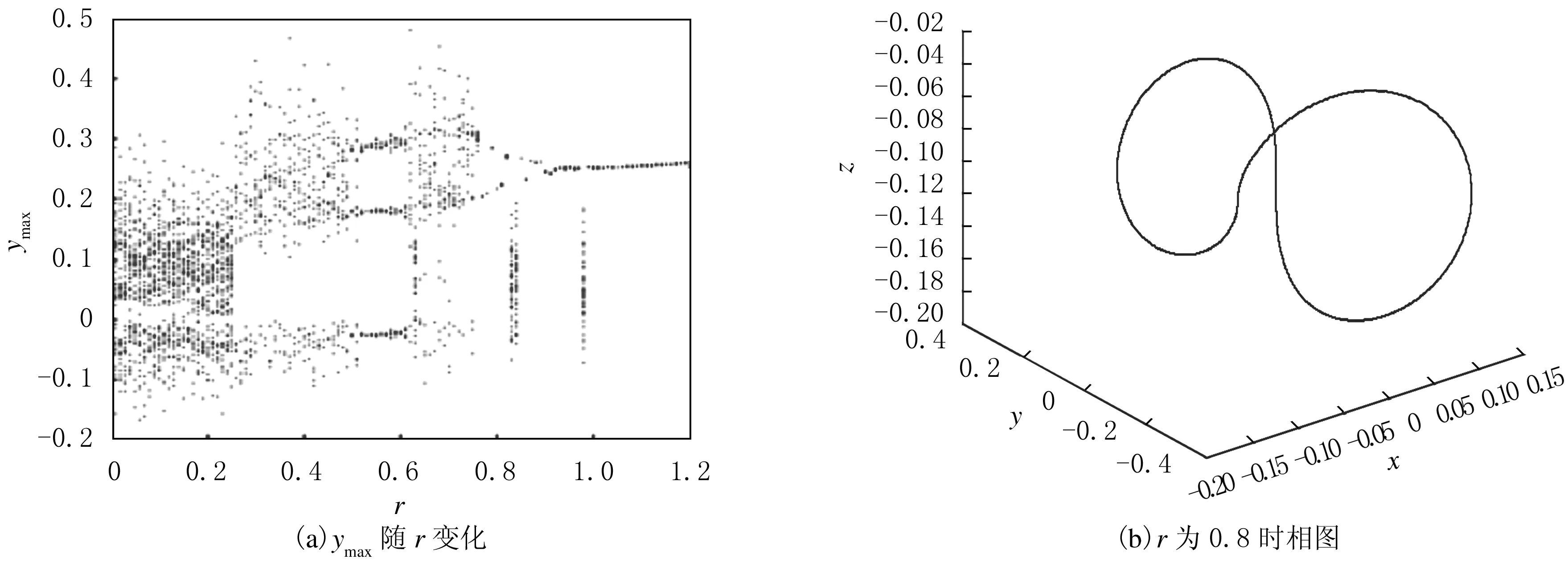
图7 参数周期扰动控制

3 初始条件影响

由于双吸引子结构特殊，受初始条件影响较大，不同初始条件对应上、下2个不同的吸引子，在控制过程中可能被吸引于不同的吸引域内，因而控制时达到的状态有可能不同.当初始条件不同时，比较2种控制方法的控制结果.

对于周期激励控制，当ω=5.0时，初始条件分别取 (0.349,0,-0.160)T和(0.349,0,-0.180)T时，控制结果与r变化关系见图8.由图8可以看出，2种方法存在一定差异.r=0.4时的控制相图见图9(a)，分别处于混沌和1周期运动状态.r=0.55时的控制相图见图9(b)，分别处于1周期和混沌运动状态.当r=0.6时均为1周期运动，且2条曲线完全重合，说明初始条件不同的2个吸引子最终控制的结果相同.

图8 ω为5.0时周期激励控制ymax随r变化图

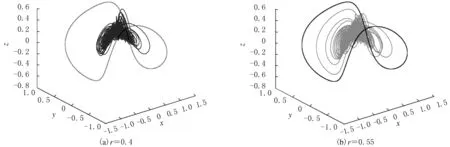
图9 不同r时的相图

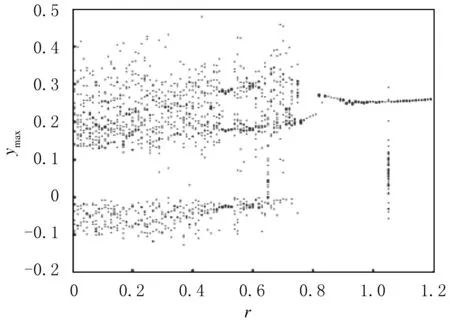
图10 参数周期扰动控制

计算参数扰动控制，当T=7.3(ω=T/(2π))、初始条件取(0.349,0,-0.180)T时，控制结果见图10.由图10与图8可以看出，在参数取某些特定值时，控制结果不同.对双吸引子复杂系统，初始条件的微小变化对应系统的上、下2个吸引子，控制对系统性质有一定影响，致使控制结果出现差异，但对结果影响不大，可控区域重合范围较大.

4 结论

(1)分析Newton-Leipnik双吸引子系统的动力学性质，5个不稳定平衡态的存在导致该系统的性质较为复杂.采用周期激励和参数周期扰动2种无反馈的控制法，研究该系统的混沌态控制，结果表明2种方法均可实现对该系统的混沌控制.

(2)2种方法的优点是无需预先了解体系的性质，即可对体系的混沌态进行控制，得到的稳定的周期轨道并不是原系统的周期轨道，系统的动力学性质发生变化.由于双吸引子系统的复杂性质，具有对初始条件的高度敏感依赖性，对比不同初始条件下的2种混沌控制方法得到的结果，表明初始条件不同对控制结果有一定影响，但影响不大.

(3)实际复杂的混沌系统很难预先了解动力学特性，为解决这类问题的混沌控制提供依据，并且在混沌控制过程中能够得到丰富的信息及新的动力学行为.