初始几何缺陷对海底管道横向屈曲的影响
刘羽霄, 葛 涛, 李 昕, 周 晶
( 1. 山东工商学院 管理科学与工程学院,山东 烟台 264005; 2. 山东工商学院 工商管理学院,山东 烟台 264005; 3. 大连理工大学 海岸与近海工程国家重点实验室,辽宁 大连 116023 )
0 引言
随着深水和边际海洋油气田的开发,越来越多高温/高压海底管道应用于工程实际.海底管道在内压和温度等工作荷载作用下,易发生整体屈曲.对于埋设在海床以下的管道,易发生垂向隆起屈曲;对于直接铺设在海床上的管道,易发生水平横向屈曲.
Hobbs R E给出理想直管道隆起及横向屈曲临界荷载的计算公式,其研究基于小坡角、线弹性假设,且没有考虑初始几何缺陷的影响[1].Taylor N等对海底管道的隆起屈曲进行理论和实验研究,针对3种不同的缺陷,分别给出管道的临界屈曲荷载,并通过实验结果对理论研究进行验证[2].James G A C采用简化模型研究隆起热屈曲,考虑初始几何缺陷及残余应力影响,给出管道隆起屈曲段的临界荷载的计算公式[3].刑静忠等研究部分悬跨管道的悬跨段和埋地段的临界屈曲荷载和变形[4].刘润等基于编制的软件探讨地基土摩阻力、管道上覆土厚度对埋地管道安全温度的影响及膨胀弯的作用[5].贾旭等研究海底管道在静水压力下的局部屈曲问题[6].苗同臣等分析初始弯曲变形对A型石油井架稳定性的影响[7].
整体屈曲理论公式仅用于判断初始几何缺陷对管道临界屈曲荷载的影响,无法用于判断初始几何缺陷对管道后屈曲的变形、应变及弯矩的影响.对于初始几何缺陷对管道后屈曲的影响分析需要采用有限元方法,如基于有限元分析软件ANSYS、ABAQUS等建立海底管道整体屈曲分析的有限元模型.初始几何缺陷是海底管道整体屈曲分析中的关键因素,基于有限元分析软件建立的海底管道整体屈曲分析的有限元模型,必须引入几何缺陷才能进行整体屈曲分析.关于海底管道横向屈曲问题的相关研究较少,基于ANSYS软件建立平坦海床上裸铺管道的非线性有限元模型,分析建模过程中初始几何缺陷的引入方法,以及初始几何缺陷幅值及缺陷长度对管道前屈曲及后屈曲的影响,以对海洋管道工程设计提供指导.
1 裸铺管道非线性有限元模型
1.1 管道模型
为了研究管道材料非线性的影响,选择PIPE20单元模拟管道.整体屈曲分析主要研究屈曲段的变形,因此管道屈曲段单元长度取1倍管道外直径,屈曲段之外单元长度逐渐增加.
管道钢的材料应力应变关系采用Ramberg-Osgood本构关系[8-9],可以表示为
(1)
(2)
(3)

图1 X65号钢应力-应变关系
式中:n为材料的硬化系数;σR为Ramberg-Osgood应力;下标1和2分别代表屈服强度和极限抗拉强度对应的应力-应变点;E为弹性模量.X65号钢的应力-应变关系见图1.
1.2 土体模型
由于土体的高度非线性及管道易变形,管-土之间的相互作用复杂.所建立的非线性有限元模型中,土体采用弹簧单元模拟.对于平坦海床上裸铺管道的横向屈曲,因管道的屈曲主要在水平面内发生,因此只需要建立二维平面模型.为了模拟土体的非线性摩擦特性,选用COMBIN39号弹簧单元.
海床与管道之间的非线性弹塑性的轴向/横向相互作用力采用弹簧单元模拟,土弹簧单元的力-位移关系见图2.其中:Fly为屈服力,Δly为屈服位移.海床与管道之间相互作用的轴向/横向摩擦力采用库仑定律计算[10]:
F=μW,
(4)
式中:F为土弹簧对应的屈服力;μ为管道与海床之间的摩擦因数;W为单位长度管道的有效重力.
1.3 管道与海床的相互作用模型
基于ANSYS软件,建立平坦海床上裸铺管道的非线性有限元模型[9-12],管-土相互作用模型见图3.主要研究管道横向的屈曲,模型中约束管道竖向的运动.根据实际模拟情况,管道两端采用完全约束或自由边界条件,主要考虑压力及温度荷载.引入初始几何缺陷后的管道有限元剖分见图4.
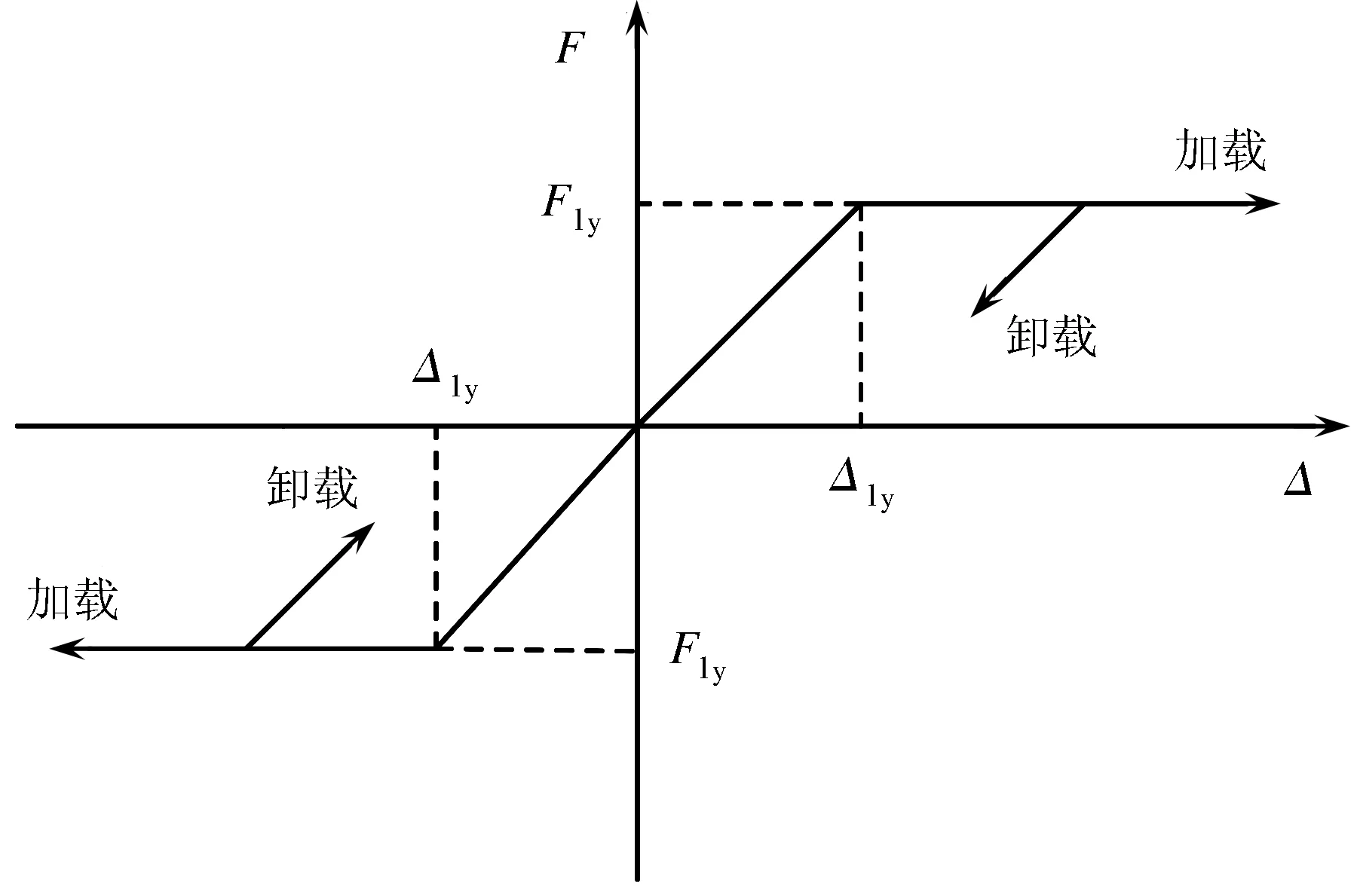
图2 土弹簧的力-位移关系
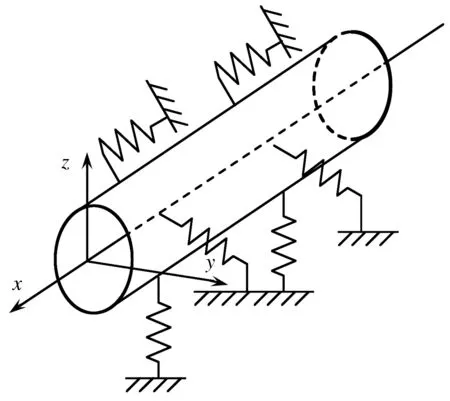
图3 管-土相互作用模型
2 初始几何缺陷
2.1 形状
数值分析中采用管道初始几何缺陷的形状[3,11]见图5.

图4 管道有限元剖分

图5 管道初始几何缺陷形状
(5)
式中:y0为缺陷段相对于x轴的横向变形;w0为初始几何缺陷幅值;L0为初始几何缺陷长度.
屈曲幅值与屈曲段长度之间的关系[2]为
(6)

(7)
式中:μl为管道与海床间的横向摩擦因数;wm为屈曲幅值,wm=y|x=0.
2.2 引入方法
2.2.1 建模引入

图6 含初始几何缺陷的管道模型
此种方法在建立管道有限元模型时引入初始缺陷,即管道初始轴向力为零[11](见图6).在计算过程中,忽略管道形成初始几何缺陷时在管道中产生的残余应力的影响.此种方法适用于在铺设管道时人为设置缺陷,且管道设置缺陷后其轴向力为零的情况.
2.2.2 加载引入
此种方法在加载过程中引入初始几何缺陷,考虑管道形成初始缺陷时引起的残余应力影响.它适用于
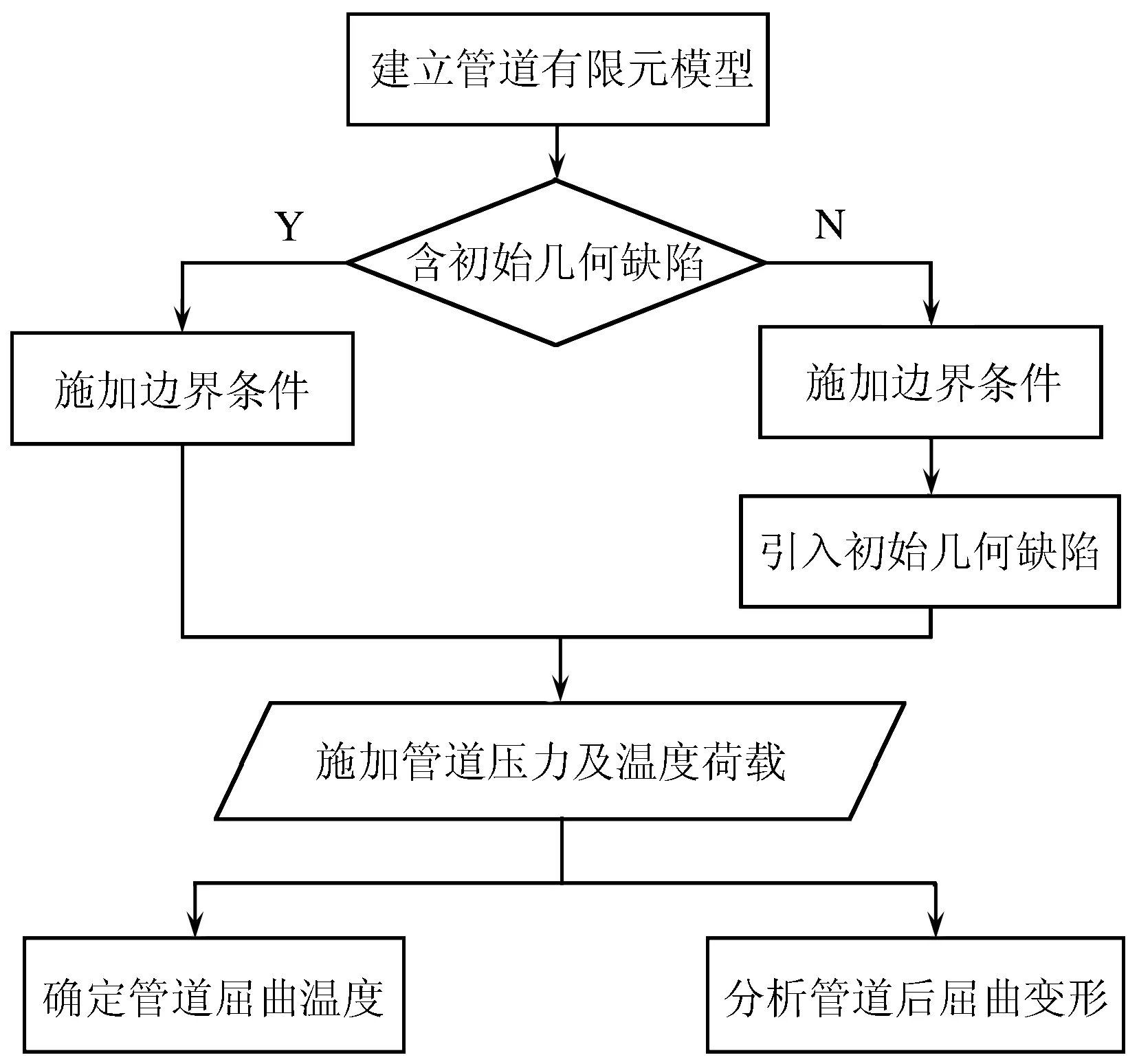
图7 管道非线性有限元分析流程
管道在铺设时为直管道,在铺设过程中或在管道运行过程中形成随机几何缺陷的情况.加载及引入缺陷的流程[9]:
(1)施加管道淹没重力、静水压力和有效残余力.
(2)通过移动管道节点和弹簧节点施加初始缺陷.
(3)释放缺陷段管道节点的约束.
(4)释放管末端.在步骤(3)之后,步骤(4)之前,约束轴向弹簧.
(5)施加内压荷载.
(6)施加温度荷载.
2.3 横向屈曲数值分析
结合初始几何缺陷的引入方法,给出管道非线性有限元分析流程(见图7).
2.4 结果分析
2.4.1 缺陷幅值
缺陷是引发管道整体屈曲的关键因素,这里所取缺陷长度为100 m,缺陷幅值分别为0.8,1.0,1.2,1.5 m.数值分析时管道相关参数见表1.

表1 管道相关参数
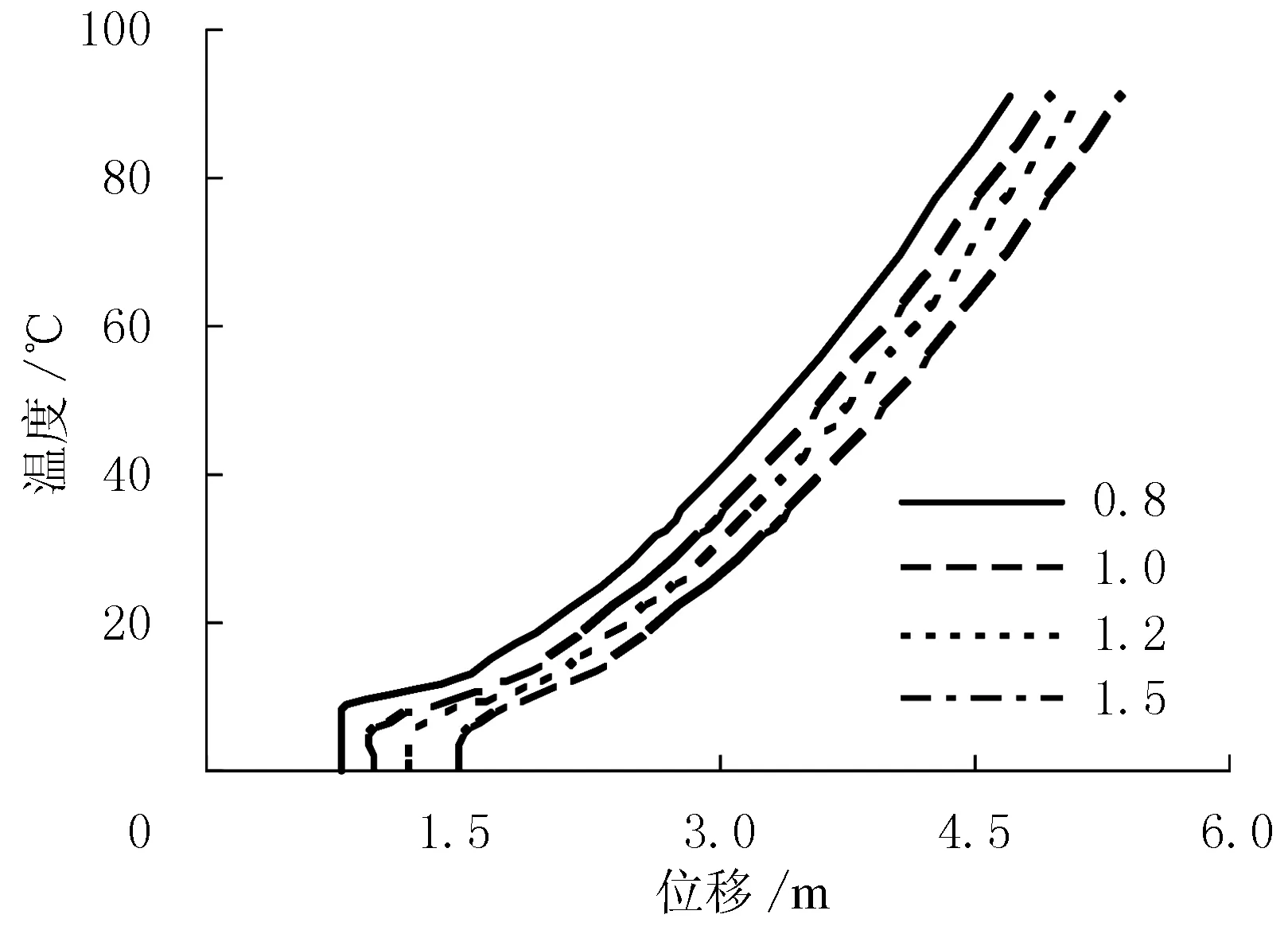
图8 不同初始缺陷幅值时的温差-最大横向位移曲线
不同初始几何缺陷幅值时的温差-最大横向位移曲线见图8.由图8可见,初始几何缺陷幅值对管道前屈曲临界温差有明显影响,临界温差随着初始几何缺陷幅值的增加而降低.
达到目标温度时不同初始缺陷幅值对管道后屈曲响应的影响曲线见图9.由图9可见,初始几何缺陷幅值对管道后屈曲的变形、弯矩、轴向应变影响不大.
2.4.2 缺陷长度
缺陷幅值为0.8 m,初始几何缺陷长度为52,64,80,100,110 m时临界温差变化曲线见10.由图10可见,临界温差随着缺陷长度的增加呈现先降低后增加的趋势.


图9 不同初始几何缺陷幅值对后屈曲响应的影响曲线

图10 不同初始几何缺陷长度时的临界温差变化曲线
达到目标温度时初始几何缺陷长度对管道后屈曲响应的影响曲线见图11.由图11可见,在缺陷幅值一定时,改变缺陷长度对管道后屈曲的变形、弯矩及轴向应变影响不大.
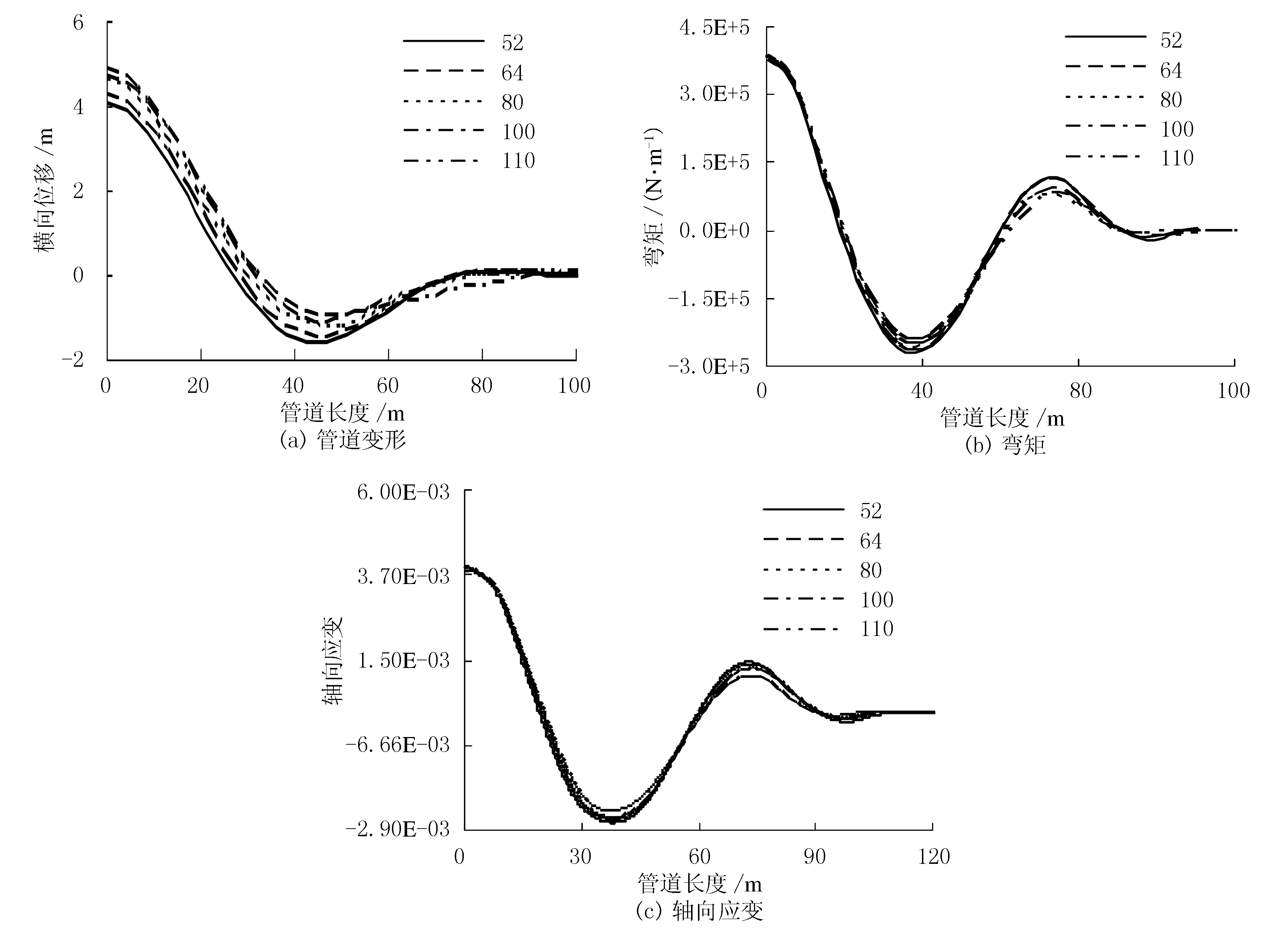
图11 不同初始缺长度对后屈曲响应的影响
3 结论
(1)基于ANSYS软件建立平坦海床上裸铺管道的非线性有限元模型,分析建模过程中初始几何缺陷的引入方法,以及初始几何缺陷幅值及缺陷长度对管道前屈曲及后屈曲响应的影响.
(2)改变初始几何缺陷幅值对管道前屈曲临界温差有明显影响;临界温差随着初始几何缺陷幅值的增加而降低,对管道后屈曲的变形、弯矩、轴向应变影响不大.
(3)临界温差随着缺陷段长度的增加呈现先降低后增加的趋势;在缺陷幅值一定时,改变缺陷段长度对管道后屈曲的变形、弯矩及轴向应变影响不大.

