一类概率依赖的不完全测量非线性系统的H∞滤波
,
车 艳 舒慧生
(1.莆田学院电子信息工程学系,福建莆田351100;2.东华大学信息学院,上海 201620)
一类概率依赖的不完全测量非线性系统的H∞滤波
,
车 艳 舒慧生
(1.莆田学院电子信息工程学系,福建莆田351100;2.东华大学信息学院,上海 201620)
阐述了一类具有不完全测量的,随机离散非线性系统的H∞滤波问题.不完全测量信息包括了测量数据丢失和随机发生地通讯延时.通过一组Kroneckerδ函数,采用一个测量输出方程同时描述了网络化控制系统中随机出现地通讯时延和测量数据丢失现象.文章的目的是使得对所有允许的时滞、测量数据丢失、随机非线性及系统内外部随机扰动,滤波误差动态系统满足均方指数稳定和H∞范数约束.最后,通过数值例子来证明文章所述H∞滤波器的有效性.
不完全测量;测量数据丢失;随机通讯时延;H∞滤波;网络化控制系统
0 引 言
本文研究了一类具有不完全测量的,随机离散非线性系统的H∞滤波问题.首先阐述H∞性能指标.众所周知,它是用来估计系统干扰抑制水平的.在过去三十年中,自Zames[1]开创性研究以来,H∞控制、滤波理论得到了快速发展[2-10],尤其是1988年Doyle等人[11]在美国控制年会上发表了著名的DGKF论文,证明了H∞控制器设计问题归结为求解两个适当的Riccati方程.同样,已经证明H∞滤波问题的可解性对于线性情况归结为一个适当的Riccati不等式,对于非线性情况归结为一个Hamilto-Jacobi不等式.
非线性存在于几乎所有的现实系统中,对于状态方程或量测方程是非线性时,为了简化系统模型和研究方便,现有文献对非线性增加了不同的约束条件,广泛采用的如Lipschitz条件[12-13].本文考虑的是扇形有界非线性,Lipschitz条件作为其特例,使得这一非线性的描述,更具一般性,更加贴近实际工程情况.
不完全测量包括了测量数据丢失和随机发生地通讯延时.在各类网络化控制系统中,例如因特网,传感器网络等,多个网络节点共享网络信道,由于网络带宽有限且网络中的数据流量变化不规则,当多个节点通过网络交换数据时,常常出现数据碰撞、多路径传输、连接中断、网络拥塞等现象,因而不可避免地出现信息交换时间延迟及丢包现象.本文通过一组Kroneckerδ函数,建设性地用一个测量输出方程同时描述了网络化控制系统中随机出现地多重时延和测量数据丢失现象.通过仿真证明了文章所述H∞滤波器的有效性.
1 问题描述
考虑下面一类随机离散非线性系统:

其中x(k)∈ℜn是状态向量,y(k)∈ℜp是测量输出,z(k)∈ℜq是要估计的系统输出,ω(k)是定义在概率空间(Ω,F,{Fk∈I+},P)上的一个一维零均值Gaussian白噪声序列并且满足Eω(k)2=1,υ(k)∈ℜp,是外部随机信号,A,Bi,C,Di,E1,E2,E3,L1是相适维已知矩阵,di∈I+(i=1,2,…,q)是已知时延满足d1<d2<…<dq,为研究方便设d0=0,Ψ(k)是给定初始条件.
{τk}是独立同分布的随机变量,表示在时刻k发生时延的大小及测量丢失的概率[14].δ(τk,di)是Kronecker delta函数满足:

φi(·)和¯φi(·)是满足下列扇形有界条件的非线性函数:

其中Ni与(i=1,2,…,q)是已知正对角矩阵.
对系统(1)设计如下一般形式的线性滤波器:
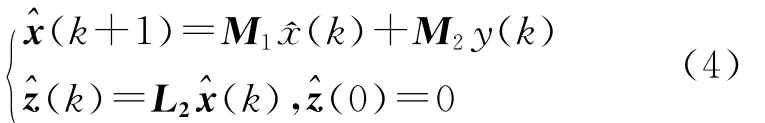
其中^x∈ℜn是状态估计,^z(k)是z(k)的估计,M1与M2是待设计滤波器参数,L2是已知相适维矩阵.设ξ(k)=[xT(k)^xT(k)]T,~z(k)=z(k)-^z(k),可有增广系统:

为研究式(5)的随机稳定性,做下面定义:
定义1 在υ(k)=0的情况下,如果存在常数α>0,β∈(0,1),使得

则滤波误差动态系统(5)称为均方指数稳定.
本文的目的是为系统(1)设计一个如(4)所示的H∞滤波器,使得下面两个条件同时满足:
(R1)滤波误差动态系统(5)均方指数稳定;
(R2)给定标量γ>0,对于所有非零ν(k),在零初始条件下,滤波误差~z(k)满足

2 主要成果
引 理 1 定 义 Ξ (k): =[ξT(k) ξT(k-1) … ξT(k-dq)]T.考虑下面Lyapunov候选函数

其中P,Q是正定矩阵,Z在(6)中有定义,如果存在标量φ>0使得

则滤波误差动态系统(5)是均方指数稳定.
证明:据式(9)有

对任一整数N≥dq+1,对式(12)两边从0至N-1关于k求和有


因此,滤波误差动态系统(5)满足定义1,是均方指数稳定,至此引理1证明完成.
定理1 给定扰动衰减γ>0和滤波参数M1和M2.如果存在正定矩阵P=PT>0,Q=QT使得矩阵不等式(21)成立,则v(k)=0系统(5)均方指数稳定且滤波误差~z(k)满足H∞条件(8).

证明:首先处理υ(k)=0情况下式(5)的稳定性分析,选择与式(9)相同的Lyapunov泛函,通过定义V(k)差分有


至此,由引理1知滤波误差系统(5)均方指数稳定.
下面处理υ(k)≠0情况,容易得到

说明式(5)是均方指数稳定,因此在零初始条件下有

至此,证明完成.
下面的定理2为滤波器参数的设计提供了一个充分条件,为了简洁,定理的证明在此略去.
定理2 给定扰动衰减γ>0,滤波误差系统(5)在υ(k)=0时均方指数稳定;并且滤波误差~z(k)在零初始条件下及任意非零υ(k)下,如果存在正定矩阵R=RT>0,S=ST>0,Q=QT>0,实数矩阵Q1,Q2与Q3使得式(31)成立,则(5)均方指数稳定.


综上所述,文章为非线性随机系统(1)关于测量丢失和随机发生的通讯时延完成了H∞滤波器的设计.值得说明的是包含了线性对象和LMIs的式(31)很容易通过常用的数值软件解得.
3 数值例子
本节通过数值例子来说明文章所提出理论的有效性.
给定系统(1)的参数如下:


仿真时,设置初始条件为x(-2)=[0.1 -0.1]T,x(-1)= [0.2 -0.2 ]T,x(0)=[0.3 -0.3 ]T.仿真结果详见图1与图2,图1是实际测量输出和理想测量输出的比较,图2是滤波误差.仿真结果证明本文所述滤波器性能很好.

图1 实际测量输出y1(1,k)与理想测量输出y2(1,k)Fig.1 Actual measurements y1(1,k)and ideal measurements y2(1,k)

图2 滤波误差~z(2,k)Fig.2 Filtering eror~z(2,k)
[1]Zames G.Feedback and optimal sensitivity:model reference transformations,multiplicative seminorms,and approximate inverses[J].IEEE Transactions on Automatic Contr,1981,26(2):301-320.
[2]Nguang S K.Robust nonlinear H∞output feedback control[J].IEEE Transactions on Automatic Control,1996,41(7):1003-1007.
[3]Nguang S K,Shi P.Nonlinear H∞filtering of sampled-data systems[J].Automatica,2000,36:303- 310.
[4]Berman N,Shaked U.H∞control for discrete-time nonlinear stochastic systems[J].IEEE Transactions on Automatic Control,2006,51(6):1041-1046.
[5]Berman N,Shaked U.H∞-like control for nonlinear stochastic systems[J].Systems &Control Letters,2006,55(3):247-257.
[6]Wang Z,Yang F,Ho D W C,et al.Robust H∞filtering for stochstic time-delay systems with missing measurements[J].IEEE Trans Signal Processing,2006,54:2579-2587.
[7]Dong H,Wang Z,Gao H.Robust H∞filtering for a class of nonlinear networked systems with multiple stochastic communication delays and packet dropouts[J].IEEE Trans Signal Processing,2010,58(4):1957-1966.
[8]Wang Z,Lam J,Ma L,et al.Variance-constrained dissipative observer-based control for a class of nonlinear stochastic systems with degraded measurements[J].Journal of Mathematical Analysis and Applications,2011,377:645-658.
[9]Shen B,Wang Z,Hung Y S,et al.Distributed H∞filtering for polynomial nonlinear stochastic systems in sensor networks[J].IEEE Trans Industrial Electronics,2011,58(5):1971-1979.
[10]吴云韬,舒娟娟,黄龙庭,等.基于状态空间实现的EDS频率与时延联合估计[J].武汉工程大学学报,2011,33(1):71-74.
[11]Doyle J,Glover K,Khargonekcar P,et al.Statespace solutions to the standard H2and H∞control problems[J].IEEE Transaction Automatic Control,1989,34(8):831-847.
[12]Yaz E E,Yaz Y I.State estimation of uncertain nonlinear stochastic systems with general criteria[J].Applied Mathematics Letters,2001,14(5):605-610.
[13]Yang F,Wang Z,Ho D W C,et al.Robust H2filtering for a class of systems with stochastic nonlinearities[J].IEEE Transactions on Circuits and Systems II,2006,53(3):235-239.
[14]He X,Wang Z,Zhou D.Network-based robust fault detection with incomplete measurements[J].International Journal of Adaptive Control and Signal Processing,2009,23:737-756.
Probability-dependent H∞fltering for a class of nonlinear systems with incomplete measurements
CHEYan1,2,SHUHui-sheng2
(1.Department of Electronics and Information Engineering,Putian University,Putian 351100,China;2.College of Information Sciences and Technology,Donghua University,Shanghai 201620,China)
TheH∞filtering problem is discussed for a class of nonlinear stochastic discrete systems with incomplete measurements.The considered incomplete measurements include both the missing measurements and the communication delays of random occurrences.By using a set of Kronecker delta functions,a unified measurement model is employed to describe the phenomena of random communication delays and missing measurements in networked control systems.The purpose of the problem addressed is to design anH∞filter such that,for all nonlinearities,incomplete measurements,internal and external disturbances,the filtering error dynamics is exponentially mean-square stable and theH∞-norm requirement is satisfied.A numerical example is given to illustrate the effectiveness of the proposed filter scheme.
incomplete measurements;missing measurements;randomly occurring communication delays;H∞filtering;networked control systems
TP202
A
10.3969/j.issn.1674-2869.2011.11.025
1674-2869(2011)11-0099-06
2011-04-24
国家自然科学基金项目(No.60974030);福建省教育厅科技项目(No.JA11211)
车 艳(1970-),女,黑龙江双城人,硕士,在读博士.研究方向:网络化系统的随机控制、数据库(分布式数据库)及应用技术、计算机操作系统.
本文编辑:龚晓宁

