孔洞形态对镍基单晶合金蠕变行为的影响
张 姝,田素贵,梁福顺,于莉丽,钱本江
(1. 沈阳工业大学 材料科学与工程学院,沈阳 110023;2. 沈阳化工学院 机械工程学院,沈阳 110142)
孔洞形态对镍基单晶合金蠕变行为的影响
张 姝1,2,田素贵1,梁福顺1,于莉丽1,钱本江1
(1. 沈阳工业大学 材料科学与工程学院,沈阳 110023;2. 沈阳化工学院 机械工程学院,沈阳 110142)
通过蠕变性能测试及组织形貌观察,研究不同形态孔洞缺陷对单晶镍基合金蠕变性能的影响,针对合金中存在有/无裂纹孔洞等铸造缺陷,对高温蠕变期间近有/无孔洞区域的应力分布进行有限元分析,根据拉应力载荷下近孔洞区域的微观应力分布特性,分析不同形态孔洞区域应力分布对单晶合金蠕变行为及组织演化的影响。结果表明:在高温蠕变期间,近有/无裂纹孔洞区域的应力分布对合金中γ′相筏形化的形态有明显影响,在有/无裂纹孔洞两侧极点处,存在最大应力值,且可致使其裂纹沿垂直于应力轴方向发生萌生与扩展;与无裂纹孔洞相比,在有裂纹孔洞两侧的极点处应力值较大,随着蠕变的进行,在较大应力处易于发生裂纹的扩展是合金具有较低蠕变寿命的主要原因。
单晶;镍基合金;孔洞形态;有限元分析;应力分布;蠕变寿命
单晶镍基合金由于具有高体积分数的γ′相及良好的高温性能,已被广泛用于制备航空发动机的叶片部件。研究表明[1−2]:单晶合金的γ′相在蠕变期间发生复杂的组织演化,并对蠕变性能有明显影响,特别是在高温低应力拉应力蠕变期间,[001]取向镍基单晶合金中γ′相沿垂直于应力轴方向形成N−型筏状组织,可有效阻碍位错运动,提高合金的高温蠕变抗力[3−4]。在单晶部件制备期间,由于凝固条件的差别,合金会形成某些组织缺陷,如孔洞、夹杂及微裂纹等[5−7]。由于孔洞或微裂纹的存在破坏了合金组织的连续性,使应力传递受到影响,并易于产生应力集中[8−9],故可促进裂纹的萌生和扩展,降低单晶合金的蠕变寿命[10−12]。但在蠕变期间,孔洞或微裂纹周围的应力分布特征及其对组织演化和蠕变特征的影响并不清楚,特别是不同形态的孔洞在蠕变期间产生不同的应力分布,并对组织演化特征产生不同的作用,但不同形态组织缺陷降低合金蠕变性能的程度并无文献报道。
因此,本文作者对成分相同和有/无裂纹孔洞缺陷的合金进行了蠕变性能测试及组织形貌观察,考察孔洞缺陷对合金中γ′相演化及蠕变寿命的影响程度,并采用有限元方法分析近不同形态孔洞区域的应力分布特征及对组织演化规律的影响,试图为单晶合金的应用提供理论依据。
1 实验
在高温度梯度真空定向凝固炉中,以选晶法将成分为Ni-6.0Al-6.5Cr-6Mo-6.5Ta-7.5W(质量分数,%)的母合金制备成[001]取向的单晶试棒,合金选用的热处理工艺如下:(1 280 ℃,6 h)+(1 325 ℃,4 h,空冷)+(1 040 ℃,4 h,空冷)+(870 ℃,24 h,空冷)。
完全热处理后的合金经Laue背反射法测定晶体取向后,沿平行于[001]取向切取片状拉伸蠕变试样,样品的宽面为(100)晶面,其横断面为4.5 mm×2.5 mm,标距为15 mm。将样品机械研磨及抛光后,置入GTW504型高温蠕变/持久试验机中,进行单轴恒定载荷拉伸蠕变曲线测定,并对有/无组织缺陷合金蠕变断裂后进行SEM形貌观察。采用ANSYS软件对近有/无裂纹孔洞区域的应力分布进行有限元分析,通过对蠕变期间合金中近有/无裂纹孔洞区域应力分布的分析,研究应力分布特征对合金中γ′相的演化及蠕变寿命的影响规律。
2 结果与分析
2.1 合金的蠕变特征及组织演化
由于选用合金在熔炼及铸造期间存在局部组织的不均匀性,并使单晶合金中产生孔洞缺陷。在高温低应力蠕变期间,其铸造期间形成的孔洞缺陷破坏了合金组织的连续性,并易于产生应力集中,故可明显降低合金的蠕变寿命。同成分有/无孔洞缺陷合金在1 072 ℃、137 MPa条件下的蠕变曲线如图1所示。

图1 孔洞对单晶合金蠕变性能的影响Fig.1 Influence of cavity defect on creep properties of single crystal alloy
图1中曲线1为无缺陷合金,曲线2为有孔洞缺陷合金,曲线3为带微裂纹孔洞合金,比较可知:无缺陷合金具有较低的应变速率和较长的蠕变寿命,其蠕变寿命长达98 h,应变量约为17%,而有孔洞缺陷合金的蠕变寿命仅有43 h,蠕变应变量降低到7.5%,带有微裂纹孔洞合金的蠕变寿命仅有38 h。即合金制备中形成的孔洞缺陷,可明显降低合金的塑性及蠕变寿命。
单晶镍基合金的铸态组织是由尺寸不均匀的γ′相和γ基体两相组成,在枝晶干区域,γ′相尺寸较小,而在枝晶间区域尺寸较大[13]。经高温固溶及四级完全热处理后,合金的组织结构是规则排列的立方γ′相以共格方式嵌镶在γ基体相中,如图2(a)所示,膜面的法线方向为[100]取向,照片中黑色区域为γ′相,白色为γ基体相。可以看出,其立方γ′相的平均边长约为0.4 μm,且均匀地沿〈100〉取向规则排列,立方γ′相的体积分数约为68%,γ基体通道的宽度约为50 nm。
在1 072 ℃、137 MPa条件下,无孔洞缺陷单晶合金蠕变98 h断裂后,在远离断口区域的组织形貌如图2(b)所示,施加应力的方向如图2(b)中箭头所示,可以看出,在高温蠕变期间,伴随合金基体中位错运动的同时,合金中γ′相经历了由立方体形态逐渐转变为筏状形态的过程,其形成的筏状γ′相及γ基体相的厚度尺寸增加。由于形成筏状γ′相取向与施加的应力轴垂直,故可有效阻碍位错运动,提高合金的蠕变抗力。

图2 不同状态单晶合金的组织形貌Fig.2 Morphologies of single crystal nickel-base superalloy at different states: (a) Fully heat-treated; (b) After crept up to fracture, γ′ phase transformed into rafted structure along direction vertical to applied stress axis
2.2 单晶合金中孔洞的形貌
对蠕变寿命较低样品进行组织形貌观察表明,合金中存在较多的组织缺陷,其中存在的圆形孔洞缺陷形貌如图3所示。施加应力轴的方向如图3所示,并认为合金具有较低蠕变寿命的原因是存在较多诸如孔洞等缺陷所致。
在远离断口的区域,合金中的γ′相已经形成与应力轴垂直的N−型筏状形貌,其中有一圆形孔洞如图3(a)所示,由于该区域远离断口,形变量较小,孔洞周围的筏状γ′相,其取向无明显差别。而在近断口区域,由于该区域形变量较大,发生缩颈,合金中的圆形孔洞已转变成椭圆状,且在孔洞左右两侧存在裂纹,如图3(b)所示。由图3(b)可以看出,孔洞周围的γ′相已形成筏状组织,但筏状γ′相的取向各异,形状较为复杂。在近孔洞的上、下区域,筏状γ′相的取向与应力轴方向成近45°排列,如图3(b)中箭头所示,并在孔洞的两侧出现裂纹。如果认为,该孔洞形变前为圆形,且为合金在凝固期间形成的组织缺陷,经高温低应力蠕变,并发生较大变形及蠕变断裂后,圆形孔洞可转变成沿应力轴方向伸长的椭圆状,并在孔洞的两侧出现裂纹,同时,γ′相发生了不规则的组织演化。
在1 072 ℃、137 MPa条件下蠕变38 h断裂后,合金中不同区域存在圆形孔洞的形貌如图4所示,在远离断口区域存在孔洞缺陷的形貌如图4(a)所示,并在孔洞的两侧存在微小裂纹,施加应力的方向如图4(a)箭头所示。由图4(a)可以看出,在远离断口的区域,合金中的γ′相已经形成筏状结构,且γ′相形成的筏状取向与施加应力轴方向垂直,近孔洞周围区域的γ′相筏形化取向与孔洞周边平行。
在近断口区域,由于该区域形变量较大,发生缩颈,合金中圆形孔洞在拉应力作用下沿应力轴方向形成椭圆状,并在孔洞两侧的微裂纹已发生扩展,如图4(b)所示。由图4(b)可以看出,在近孔洞区域的γ′相已形成筏状结构,其形成筏状γ′相的取向与孔洞周边的边界平行,呈流线型分布。可以认为,合金中的圆形孔洞为凝固期间形成的组织缺陷,其两侧的裂纹为原来固有或在蠕变初期形成。随高温低应力蠕变的进行,形变量逐渐增加,样品发生缩颈直至发生蠕变断裂,故致使孔洞两侧的裂纹逐渐扩展,圆形孔洞转变成椭圆状,同时,筏状γ′相形态发生变化,但与图3(b)中筏形化γ′相沿孔洞周围呈放射状相比,形态明显不同。如果认为筏状γ′相形态的变化与孔洞周围的应力场分布有关,则有/无裂纹孔洞周围筏状γ′相呈现不同的形态,表明不同形态的孔洞周围存在不同的应力分布,其不同的应力分布对筏状γ′相的演化特征、裂纹扩展及蠕变寿命有重要影响。

图3 在1 072 ℃、137 MPa条件下合金蠕变43 h断裂后不同区域孔洞的形貌Fig.3 Morphologies of cavity in different regions of alloy crept for 43 h up to fracture at 1 072 ℃ and 137 MPa: (a) Region far from fracture; (b) Region near fracture

图4 在1 072 ℃、137 MPa条件下合金蠕变38 h断裂后不同区域孔洞的形貌Fig.4 Morphologies of cavity in alloy crept for 38 h up to fracture at 1 072 ℃ and 137 MPa: (a) Cavity with cracks in region far from fracture; (b) Cracks propagation in cavity region near fracture
3 近孔洞区域的应力分布及其对组织演化的影响
3.1 近孔洞区域的应力分布
利用有限元方法对近孔洞缺陷区域进行应力分析中,采用的Norton表达式为=Aσn,其中为等效蠕变应变率,σvon为von Mises等效应力,A和n是与温度有关的参数,计算中取A=5×10−30,n=7,材料的弹性模量和泊松比分别如下:E=200 GPa和υ=0.3[14]。根据蠕变样品的尺寸建立二维平面有限元模型,计算中对样品施加的温度为1 072 ℃,并使样品最小截面保持137 MPa的静应力。
实验用拉应力蠕变样品为板状工字形,在高温施加137 MPa条件下,1/2工字形样品中不同区域的应力分布如图5所示。由图5可以看出,在样品标距的中间区域具有最大等效应力值,其应力值为648 MPa,随着离断口距离的增加,等效应力逐渐降低。因此,蠕变断裂优先发生在样品标距的中间区域。

图5 在1 072 ℃、137 MPa条件下1/2板状样品不同区域的等效应力分布Fig.5 von Mises stress distribution in different regions of 1/2 creep specimen at 1 072 ℃ and 137 MPa
在实验的温度和施加应力条件下,计算出样品近孔洞区域的应力分布与施加载荷的时间有关,其应力分布随蠕变时间的变化规律如图6所示。设样品中存在铸态圆形孔洞缺陷,随样品蠕变至7 h,孔洞仍保持圆形,在孔洞的上、下部位具有较低的应力值,在近孔洞两侧的区域出现应力较大值为119 MPa,应力分布具有对称特征,如图6(a)所示。随着蠕变的进行,在孔洞两侧区域的应力值增大,当蠕变21 h后,孔洞两侧应力值再次增大,其 von Mises应力等值线呈蝶形分布,在孔洞两侧的极点b处仍为最大值,其值约为211 MPa,并使圆形孔洞沿施加应力方向略有伸长呈现椭圆状,如图6(b)所示。
随着蠕变的进行,在近椭圆形孔洞两侧的应力等值线呈现碟形特征,其碟形的前端与应力轴方向呈45°角伸长,极点b处的应力最大值进一步增加;随着蠕变时间的延长,孔洞两侧的等应力曲线呈碟形特征加剧,孔洞沿应力轴方向进一步伸长,在近孔洞的上、下区域为最小应力值分布区,而在孔洞两侧的最大应力值进一步增加,可促使其裂纹在孔洞两侧萌生;随蠕变时间延长至43 h,孔洞周围区域的等应力值进一步增加,致使孔洞两侧极点b处的最大应力值增加到约439 MPa,如图6 (c)所示,该值已远大于合金在1 072 ℃的屈服强度值[15],故可致使孔洞两侧发生裂纹的扩展,如图3(b)所示。
根据近孔洞区域的应力分布及随时间的变化规律,分析认为孔洞极点b区域具有最大的应力分布值,故该区域易于产生应力集中。当应力集中值增加到大于该合金的屈服强度时,可致使合金萌生裂纹,且随着蠕变的进行,应力值逐渐增大,可使裂纹沿垂直于应力轴方向逐渐扩展,其裂纹扩展的形貌如图3(b)所示。由于在近孔洞区域两侧的应力分布沿与施加应力轴呈45°方向具有较大值(该方向为施加载荷的最大切应力方向),如图6(c)所示,该应力分布特征可致使合金中筏状γ′相转变成沿较大切应力方向排列,如图3(b)中箭头所示。由于筏状γ′相层片相间,其强度较低的γ基体相与最大切应力方向平行,故可致使合金中裂纹沿强度较低的γ基体通道扩展而发生蠕变断裂。
3.2 近有裂纹孔洞区域的应力分布
在实验的温度和施加应力条件下,计算出样品中近有裂纹孔洞区域的应力分布与施加载荷的时间有关,其应力分布随时间的变化规律,如图7所示。设样品中存在铸态圆形孔洞缺陷,其中孔洞两侧带有裂纹,或为蠕变初期在孔洞两侧形成微裂纹。随样品蠕变至7 h,孔洞仍保持圆形,在孔洞的上、下部位都具有较低的应力值,在近孔洞两侧的裂纹区域出现应力最大值为131 MPa,且应力分布具有对称性,如图7(a)所示。随着蠕变的进行,在近孔洞两侧裂纹区域,应力值增大,蠕变21 h后,孔洞两侧的应力值进一步增大,在孔洞两侧的裂纹b处应力达到最大值,约为211 MPa,使圆形孔洞沿应力轴方向伸长呈现椭圆状,并使圆形孔洞两侧的裂纹扩张,如图7(b)所示。
随着蠕变的进行,孔洞两侧裂纹b处应力最大值进一步增加;随蠕变时间的延长,在近孔洞的上、下区域仍为最小应力分布区,而在孔洞两侧的应力值继续增大;随蠕变时间延长至38 h,近孔洞及裂纹区域的等应力值进一步增大,孔洞两侧裂纹极点b处的最大应力值增加至约741 MPa,如图7(c)所示,该值已远大于合金在1 072 ℃的屈服强度值,故可致使样品在近孔洞区域发生裂纹的扩展直至发生蠕变断裂。

图6 在1 072 ℃、137 MPa条件下近孔洞区域的应力分布随蠕变时间的变化规律Fig.6 Change of von Mises stress distribution near cavity region of alloy with creep time: (a) 7 h; (b) 21 h; (c) 43 h
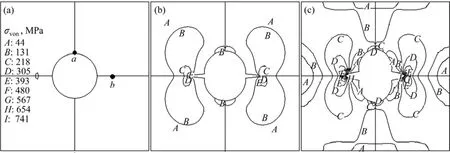
图7 在1 072 ℃、137 MPa条件下预置裂纹孔洞区域的应力分布随蠕变时间的变化规律Fig.7 Change of von Mises stress distribution near cracks-cavity region of alloy with creep time: (a) 7 h; (b) 19 h; (c) 38 h
根据近裂纹孔洞区域的应力分布随时间的变化规律,分析认为,在孔洞两侧裂纹极点b区域具有最大的应力值,故该区域易于产生应力集中。当应力集中值增加到大于该合金的屈服强度时,可致使合金中裂纹沿垂直于应力轴方向扩展,如图4(b)所示。与无裂纹孔洞应力分布的图6(c)相比,有裂纹孔洞区域具有不同的应力分布特征,前者在近孔洞区域沿应力轴的45°方向具有较大应力值,可致使合金中筏状γ′相转变成沿应力轴的45°方向排列,而后者沿孔洞边界线具有较大应力值,因此,合金中筏状γ′相沿孔洞周边呈流线型分布,如图4(b)所示;前者在孔洞两侧具有的最大应力值为439 MPa,而后者在孔洞两侧具有更大的应力值(为741 MPa),因而,后者更易于裂纹的扩展直至发生蠕变断裂。如果认为有限元分析的结果为理论预测值,则有裂纹孔洞的合金蠕变至38 h已发生蠕变断裂,具有更短的蠕变寿命,即有限元分析的理论预测值与图1的实验结果相一致。因此,可以认为,样品中的孔洞在蠕变期间为易于形成裂纹的裂纹源,且随孔洞数量的增加,蠕变期间发生裂纹萌生及扩展的几率增大,合金的蠕变寿命缩短。
3.3 蠕变期间孔洞的应变
由图6和7还可以看出,在圆形孔洞的a、b两极点处具有不同的应力分布特征,在极点b处,具有最大的应力值,该最大应力值可促使样品发生裂纹的萌生,并使其沿垂直于应力轴方向扩展。而在极点a处应力值较小,但却产生较大位移(在有限元计算中的位移量可视为沿垂直于应力轴方向的应变量),有/无裂纹孔洞合金随蠕变进行,发生的位移量不同,随蠕变进行,有/无裂纹孔洞合金在极点a处发生的位移量随时间变化呈抛物线规律增加,如图8所示。
由图8中曲线1可知,孔洞合金经蠕变43 h断裂后,应变量为7.4%,而在孔洞区域的位移量仅为0.225 μm,其值远小于合金的蠕变应变量;由图8中曲线2可知,微裂纹孔洞合金经蠕变38 h断裂后,其应变量为9.1%,而在孔洞区域的位移量为0.234 μm,其值远小于合金的蠕变应变量。比较可知,随蠕变进行,在有/无裂纹孔洞合金的极点a处的位移量不同,其中,有裂纹孔洞具有较大的位移量。如果认为,合金的蠕变应变量完全由孔洞区域的位移量构成,则单独一个孔洞区域的位移量不能构成合金的应变量。故由此可推断,该合金的蠕变应变及断裂由多个孔洞发生位移及裂纹扩展组成。同时,在合金的近裂纹区域易于产生应力集中,且随着蠕变的进行,裂纹尖端应力值增大,其产生的应力集中可促使裂纹的扩展,并直至发生蠕变断裂,其中,合金中的孔洞成为裂纹源,故含有裂纹的合金具有较短的蠕变寿命。

图8 蠕变期间近孔洞极点a处的位移随时间的变化Fig.8 Change of displacement at top of cavity with creep time
由于蠕变期间,在样品的不同区域,具有不同的应力分布值,在近断口区域,应力值较大;在远离断口区域,应力值逐渐降低。因此,在近断口区域,孔洞易于发生裂纹的萌生与扩展,而在远离断口区域,孔洞发生裂纹萌生与扩展的几率降低。当在近断口区域发生多个裂纹萌生与扩展时,其扩展的裂纹相互连接成为撕裂层,使样品承载的有效面积减小,即可发生瞬间断裂。
4 结论
1) 孔洞缺陷可明显降低单晶合金的蠕变寿命,随着蠕变的进行,圆形孔洞沿应力轴方向伸长成椭圆状,单一孔洞产生的应变量较小,合金蠕变期间的应变及断裂由多个孔洞产生的应变及裂纹扩展组成。
2) 在蠕变期间,在近孔洞区域沿应力轴方向形成对称的碟形应力分布,孔洞上部应力较小,沿应力轴45°方向有较高的应力值,是致使合金中筏状γ′相沿45°方向排列的主要原因;其中,在孔洞两侧的极点处的应力值最大,随着蠕变的进行,最大应力值增加,可促使裂纹在极点处沿垂直于应力轴方向萌生与扩展,直至发生断裂是合金的蠕变断裂机制。
3) 在蠕变期间,在近有/无裂纹孔洞区域,应力分布不同,与无裂纹孔洞相比,在有裂纹孔洞两侧的极点区域产生更大的应力值,且随着蠕变的进行,最大应力值增加,可促使裂纹易于沿垂直于应力轴方向扩展,是使合金具有较短蠕变寿命的主要原因。
REFERENCES
[1] 马文有, 李树索, 乔 敏, 宫声凯, 郑运荣, 韩雅芳. 热处理对镍基单晶高温合金微观组织和高温持久性能的影响[J]. 中国有色金属学报, 2006, 16(6): 937−944.MA Wen-you, LI Shu-suo, QIAO Min, GONG Sheng-kai,ZHENG Yun-rong, HAN Ya-fang. Effect of heat treatment on microstructure and stress rupture life of Ni-base single crystal superalloy[J]. The Chinese Journal of Nonferrous Metals, 2006,16(6): 937−944.
[2] 田素贵, 杜洪强, 王春涛, 孟凡来, 胡壮麒. W含量对单晶镍基合金组织与性能的影响[J]. 航空材料学报, 2006, 26(3):16−19 TIAN Su-gui, DU Hong-qiang, WANG Chun-tao, MENG Fan-lai, HU Zhuang-qi. Influence of W concentration on microstructure and properties of single crystal nickel base superalloy[J]. Journal of Aeronautical Materials, 2006, 26(3):16−19.
[3] 张 光, 张克实. 正交各向异性弹塑性材料中微孔洞的扩张[J]. 机械强度, 2002, 24(2): 246−249 ZHANG Guang, ZHANG Ke-shi. Modeling void growth in orthotropic elastic-plastic materials[J]. Journal of Mechanical Strength, 2002, 24(2): 246−249.
[4] WANG Yi, YUE Zhu-feng, STEIN M P. Experimental and finite element study of void growth in nickel-base single crystal superalloys[J]. Rare Metal Materials and Engineering, 2006,35(1): 39−42.
[5] 于庆民, 岳珠峰. 镍基单晶合金中空穴绕夹杂形核及后续演化的有限元分析[J]. 航空学报, 2009, 30(1): 179−181.YU Qing-min, YUE Zhu-feng. Finite element analysis on void nucleation and growth around inclusion in nickel-based single crystal superalloys[J]. Acta Aeronautica et Astronautica Sinica,2009, 30(1): 179−181.
[6] 李振环, 张克实. 光滑拉伸试件中不同初始形状孔洞长大的有限元模拟[J]. 计算力学学报, 1997, 14(4): 454−461.LI Zhen-huan, ZHANG Ke-shi. Finite element simulation on the growth of void in the smooth bar[J]. Chinese Journal of Computational Mechanics, 1997, 14(4): 454−461.
[7] GOLOGANU M, LEBLOND J B, DEVAUX J. Approximate models for ductile metals containing non spherical voids-case of axisymmetric prolate ellipsoidal cavities[J]. J Mech Phys Solids,1993, 41: 1723−1754.
[8] 田素贵, 周惠华, 张静华, 杨洪才, 徐永波, 胡壮麒. 一种单晶镍基合金的高温蠕变损伤[J]. 金属学报, 1998, 34(1): 57−63.TIAN Su-gui, ZHOU Hui-hua, ZHANG Jing-hua, YANG Hong-cai, XU Yong-bo, HU Zhuang-qi. The creep-damage behavior of a single crystal nickel-base superalloy[J]. Acta Metallurgical Sinica, 1998, 34(1): 57−63.
[9] PARDOEN T, DUMONT D, DESCHAMPS A, BRECHET Y.Grain boundary versus transgranular ductile failure[J]. J Mech Phys Solids, 2003, 51: 637−665.
[10] 温志勋, 苟文选, 岳珠峰. 镍基单晶裂纹扩展路径研究[J]. 稀有金属材料与工程, 2007, 36(9): 1549−1553.WEN Zhi-xun, GOU Wen-xuan, YUE Zhu-feng. Crack propagation paths and fracture of Ni-based single crystal[J]. Rare Metal Materials and Engineering, 2007, 36(9): 1549−1553.
[11] PARDOEN T, HUTCHINSON J W. An extended model for void growth and coalescence[J]. J Mech Phys Solids, 2000, 48:2467−2512.
[12] 管 欣, 耿小亮. 多晶体材料晶界孔洞应力场分析[J]. 西北工业大学学报, 2004, 22(6): 726−729.GUAN Xin, GENG Xiao-liang. Stress distribution near cavity on grain boundary[J]. Journal of Northwestern Polytechnical University, 2004, 22(6): 726−729.
[13] 水 丽, 田素贵, 金 涛, 胡壮麒. 预压缩单晶镍基合金的组织结构及在拉伸蠕变期间的粗化特征[J]. 稀有金属材料与工程, 2006, 35(8): 1282−1186.SHUI Li, TIAN Su-gui1, JIN Tao, HU Zhuang-qi.Microstructure of pre-compressed single crystal nickel-base superalloy and its coarsening feature during tensile creep[J].Rare Metal Materials and Engineering, 2006, 35(8): 1282−1186.
[14] 颜鸣皋. 工程材料实用手册[M]. 二版. 北京: 中国标准出版社, 2001: 792−794.YAN Ming-gao. Practical handbook of engineering materials[M].2nd ed. Beijing: China Standard Press, 2001: 792−794.
[15] EGGELER G, WIESNER C. A numerical study of parameters controlling stress redistribution in circular notched specimens during creep[J]. J Strain Analysis for Engineering Design, 1993,28: 13−22.
Influence of cavity morphology on creep behaviors of single crystal nickel-base superalloy
ZHANG Shu1,2, TIAN Su-gui1, LIANG Fu-shun1, YU Li-li1, QIAN Ben-jiang1
(1. School of Materials Science and Engineering, Shenyang University of Technology, Shenyang 110023, China;2. School of Mechanical Engineering, Shenyang Institute of Chemical Technology, Shenyang 110142, China)
By means of creep properties measurement and microstructure observation, the influence of cavity morphology on the creep behaviors of a single crystal nickel-base alloy was investigated. Due to the cavity with or without cracks exists in the as-cast superalloy, the stress distribution near the cavity with or without cracks during high temperature creep was analyzed by finite elements analysis method (FEM), and the influence of the stress distribution near the cavity regions on the creep behaviors and microstructure evolution of the superalloy was discussed according to the feature of the stress distribution near the cavity. The results show that, during high temperature creep, the stress distribution near the cavity with or without cracks has an obvious effect on the morphology of the rafted γ′ phase in the superalloy, the maximum stress value which appears in two sides of the cavity with or without cracks may promote the initiation and propagation of the cracks along the direction vertical to the applied stress axis. Compared with the crack-free cavity, the bigger stress value appears in two sides of the cavity with cracks which propagates easily as creep goes on, this is the main reason resulting in the alloy with shorter creep lifetime.
single crystal; nickel-based superalloys; cavity morphology; FEM analysis; stress distribution; creep lifetime
TG 132.2
A
1004-0609(2011)04-0762-07
2010-03-26;
2010-06-30
田素贵,教授,博士;电话:024-25494089;E-mail: tiansuguig2003@163.com
(编辑 龙怀中)

