Kriging模型在机翼气动外形优化中的应用

孙美建，詹 浩

(西北工业大学航空学院，陕西西安 710072)

0 引言

在三维气动外形优化中，由于设计变量多以及解Euler/N-S方程计算量庞大，基于梯度信息的直接优化方法仍然是飞行器气动外形优化设计的主要工具［1－3］，然而该方法比较依赖于初始模型，容易陷入局部最优。人们受自然界各种物理现象启发发展了如遗传算法、模拟退火算法、粒子群算法等随机优化算法，与直接优化算法相比具有更好的全局性和鲁棒性，但是其缺点是评价目标函数的次数远远高于直接优化算法。

基于代理模型的优化方法已经在翼型优化中得到广泛应用［4－6］，用随机优化算法与代理模型相结合，可大幅度减少流场计算的次数。本文采用改进的量子粒子群算法优化Kriging模型的相关模型参数，提高Kriging模型预测精度，并结合具有双层结构的粒子群优化算法，发展了同样适用于三维气动外形优化的高效算法。针对具有44个设计变量的跨声速机翼采用N-S方程流场求解器进行了优化验证。

1 优化算法

1.1 改进的量子粒子群算法

2004年，Sun J等人提出具有量子行为的粒子群算法(Quantum-Behaved Particle Swarm Optimization，QPSO)［7］。QPSO中粒子搜寻的位置由概率密度函数确定，而不同于标准粒子群算法(Particle Swarm Optimization，PSO)［8］按照轨道的形式进行搜索，通常 QPSO表现出更优秀的全局搜索性能。QPSO算法搜索方程可以表述为:

本文采用进一步改进的量子粒子群算法(MQPSO):每个粒子计算完成后立即更新pbest、gbest、mbest，并根据pbest进行排序，每个粒子仅向优于自身pbest的粒子学习，而且排名越靠后的粒子向其他粒子学习的程度越高。由此通过提高算法对信息的利用率，加快收敛速度。

1.2 Kriging代理模型

Kriging代理模型［10］起源于地理空间统计学，是一种估计方差最小的无偏估计模型，通过相关函数的作用，具有局部估计的特点，它可以较好地预估未知点处函数值的分布情况。Kriging模型中响应值与设计变量之间的关系可以表示为:

其中F(β，x)为回归模型由P个已知函数组合构成，

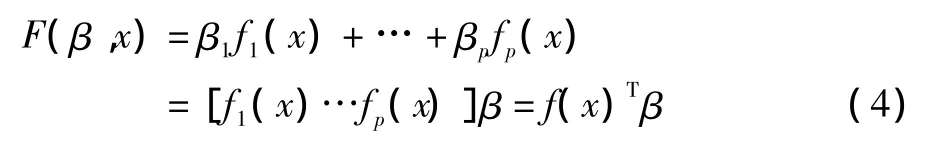
回归模型是对设计空间的全局近似，为确定性部分，通常分成0阶(常数)、1阶(线性)和2阶(二次多项式)三类模型，β为回归模型参数。

z(x)是均值为0、方差为σ2的统计随机过程，并且两个插值点的协方差为:

其中R是点x(i)和x(j)的相关函数，本文选用高斯函数表示为:

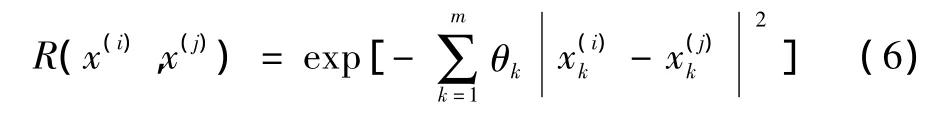
未知点x0处的预测值(x0)和方差估计值通过如下形式给出:

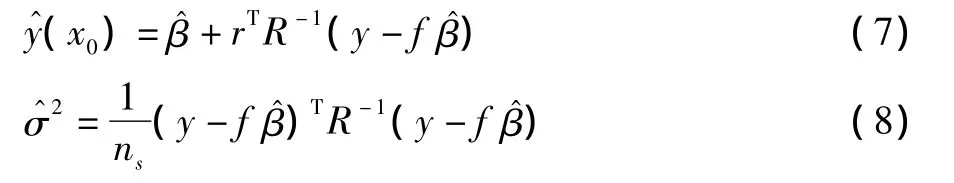
通过极大似然估计确定相关模型参数θk:

相关模型参数的选取对代理模型的性能有重要的影响，Lophaven等开发的DACE-A Matlab Kriging Toolbox［11］采用模式搜索方法求解相关模型参数，但是该方法严重依赖于初始点的选取，容易陷入局部最优。游龙海等人［12－13］采用遗传算法和粒子群算法对Kriging模型相关参数进行优化，本文采用MQPSO算法求解相关模型参数，以提高Kriging模型预测精度。

1.3 基于Kriging模型的双层量子粒子群算法

代理模型方法可以根据已有的点预测未知点的适应值分布情况，当代理模型达到一定精度时，可代替真实求解用于工程优化。传统的代理模型优化框架［14－16］如下:首先用一定数量的样本点构造代理模型，优化找到代理模型的最优解并与真实值对比，若不满足收敛要求则加入新计算的真实值更新代理模型，直到优化结束。该方法收敛速度快，但是严重依赖于代理模型预测的精度，对于复杂的高维度优化问题极容易陷入局部最优。

虽然代理模型预测精度有限，但是往往能较好地反映出真实解的大致情况。为了将代理模型获得的信息充分用于优化，本文采用如下基于Kriging模型的双层量子粒子群优化算法(KMQPSO)，该算法由两层MQPSO算法构成，并以Kriging模型为联系媒介。

首先在变量空间均匀产生具有Q个粒子的粒子池，通过CFD计算获取适应值，然后从中选取适应值最好的M个粒子作为父级MQPSO的初始种群，对种群中每个粒子按照MQPSO更新位置的方法繁殖X个个体(式(2)中 φ，u为(0，1)的随机数，所以该X 个个体位于不同的进化位置)，此时用已计算的粒子构造Kriging模型预测繁殖的粒子，选出适应值最优的粒子)，计算该粒子与父级粒子种群中最近的粒子的“欧氏距离”，据此确定一个合适的阀值半径 R，以)为中心R为半径确定一个变量区域，在该区域中嵌入种群规模为m迭代代数为n的子级MQPSO进行优化寻找代理模型的最优解，将该解作为正式进化的个体进行CFD适应值计算，完成后立即更新pbest、gbest、mbest和代理模型，直到N代父级MQPSO优化结束。

阀值半径R由下式确定:

其中，Dim为变量维数，α为控制半径的系数，以各粒子的子级区域能覆盖父级的进化区域，而相互之间又不产生过多的重叠为宜。

KMQPSO算法中具有Q个粒子的粒子池用于获得初始代理模型样本点，可以通过实验设计方法或约束由“欧氏距离”表述的相似度在解空间产生初始样本点。根据适应值排序原则选择M个粒子的方法可获得优良的初始种群而且这些粒子较均匀地分布在解空间。粒子的繁殖策略可以为子级MQPSO筛选优良的局部区域，嵌套的子级优化则有助于找到代理模型的局部最优。通过粒子的繁殖筛选和局部优化，将要进行CFD计算的粒子精准地定位于代理模型的局部最优，通过迭代更新不断提高代理模型在最优解附近的预测精度，从而收敛速度更快，而又能保持多样性保证优化精度。

2 机翼气动外形优化

2.1 参数化方法

本文采用Hicks-Henne解析函数法［17］参数化机翼剖面翼型，新翼型由基本翼型的弯度或厚度加扰动构成。本文为了减少设计变量的个数，取弯度与厚度设计变量各4个，表达如下:

以平面形状确定的大展弦比跨声速机翼为优化对象，沿展向取如图1的5个设计剖面(即沿展向η=2z/b为0、0.14、0.34、0.65 和 1.0 的机翼剖面，z为展向位置，b为展长)，每个剖面由8个设计变量控制剖面翼型形状，翼根翼剖面扭转角固定为2.8°，其他4个剖面的扭转角为设计变量，并绕1/4弦线扭转，这样整个机翼一共由44个设计变量决定。

图1 机翼设计剖面选取Fig.1 Design sections on wing planform

2.2 多目标多约束处理

评价适应值方法的选取将对优化结果产生重要影响。通常采用加权、分效能曲线加权、几何求积等方法［18］评价适应值。本文采用一种多目标非线性加权组合方法，当前评估机翼的某项性能为cnew，根据设计经验设定cbad为不可接受解，cgood为满意解，使用如下公式确定机翼的适应值:

对于几何约束问题通常采用罚函数加权方法，但是该方法会增加优化的难度。由于QPSO中粒子出现的位置不是确定的，而是由概率密度函数确定，因此可以设定循环直到产生符合几何约束条件的机翼。而对于与性能相关的约束如低头力矩的约束，本文将其作为设计目标进行优化。

2.3 Kriging模型性能测试

以设计机翼的基准翼型为设计对象，采用上述的8个设计变量的参数化方法生成400个不同的翼型，采用N-S雷诺平均方程计算绕翼型流场，湍流模型为k-ω两方程模型。选取图2中的样本点个数，剩下的作为测试样本，分别采用1阶、2阶回归模型的原始Kriging和1阶回归模型的改进的Kriging进行预测。结果表明对于原始Kriging模型，采用2阶回归模型具有较高的精度，而改进的Kriging模型则表现出更高的预测精度。

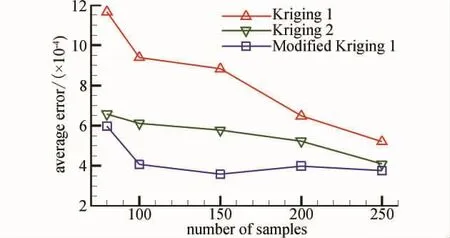
图2 Kriging模型预测翼型阻力系数的平均误差Fig.2 Average error of CDbetween forecast and CFD

Kriging模型中不同阶次的回归模型对样本点的个数有不同的要求，设变量个数为n，构造0阶的回归模型至少要1个样本，1阶至少要n+1个，而2阶至少要0.5(n+1)(n+2)个，44个设计变量将至少需要1035个样本点才能构造2阶的Kriging模型，这在机翼优化中将耗费的计算量是难以接受的。以上述的44个设计变量的机翼为设计对象，生成400个不同的机翼，采用N-S雷诺平均方程计算绕机翼流场，湍流模型为k-ω两方程模型。选取图3中的样本点个数，剩下的作为测试样本，分别采用1阶回归模型的原始Kriging和1阶的改进Kriging进行预测，改进的Kriging模型同样表现出良好的预测精度。

2.4 机翼气动外形优化算例

以上述跨声速机翼为优化对象，巡航Ma=0.785，Re=2.2 ×107，CL=0.54，多目标优化阻力系数 CD、低头力矩系数Cm以及对翼根的弯矩系数Cmx(绕机体轴，Cmx对机翼结构重量有重要影响)，加权系数δ分别为1.0、0.15、0.12，限定各剖面翼型最大相对厚度以及机翼容积不减。

图3 Kriging模型预测机翼阻力系数的平均误差Fig.3 Average error of CDbetween forecast and CFD

设置KMQPSO算法中Q为200，M为18，N为20，X随迭代从5线性增加到20，m为20，n随迭代从20线性增加到80，子级区域半径系数α随迭代从0.4线性增加到1.5，这些参数随迭代线性变化是为了在优化初期保持种群多样性，而在后期加快收敛速度。当总计算次数达400次时，适应值变化的幅度已经很小，监视设计变量值的变化发现已经表现出收敛的形态，图4是某个设计变量值收敛的情况，前200次计算是对粒子池进行的，之后在设计变量区域内进行了有效的搜索至收敛。

图5为机翼优化前后各设计剖面外形变化情况，剖面最大相对厚度和机翼容积都没有降低，而阻力、低头力矩和翼根弯矩都得到了改善。由图6机翼剖面的的压力分布可以看出，设计机翼得到无激波或极弱激波形态的压力分布，说明设计结果是理想的。

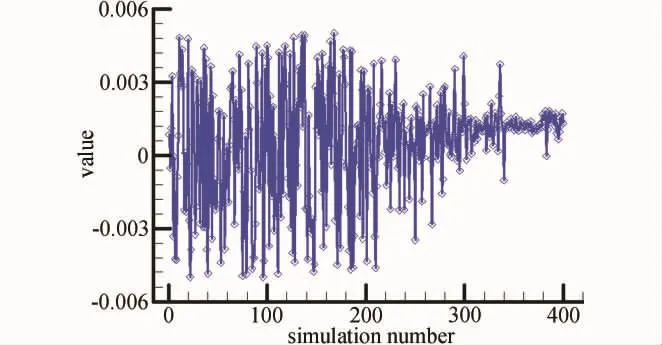
图4 某变量收敛情况Fig.4 Optimization convergence of one design parameter

图5 各剖面初始形状(虚线)与设计形状(实线)Fig.5 Wing section profiles(initial-dash，design-solid)

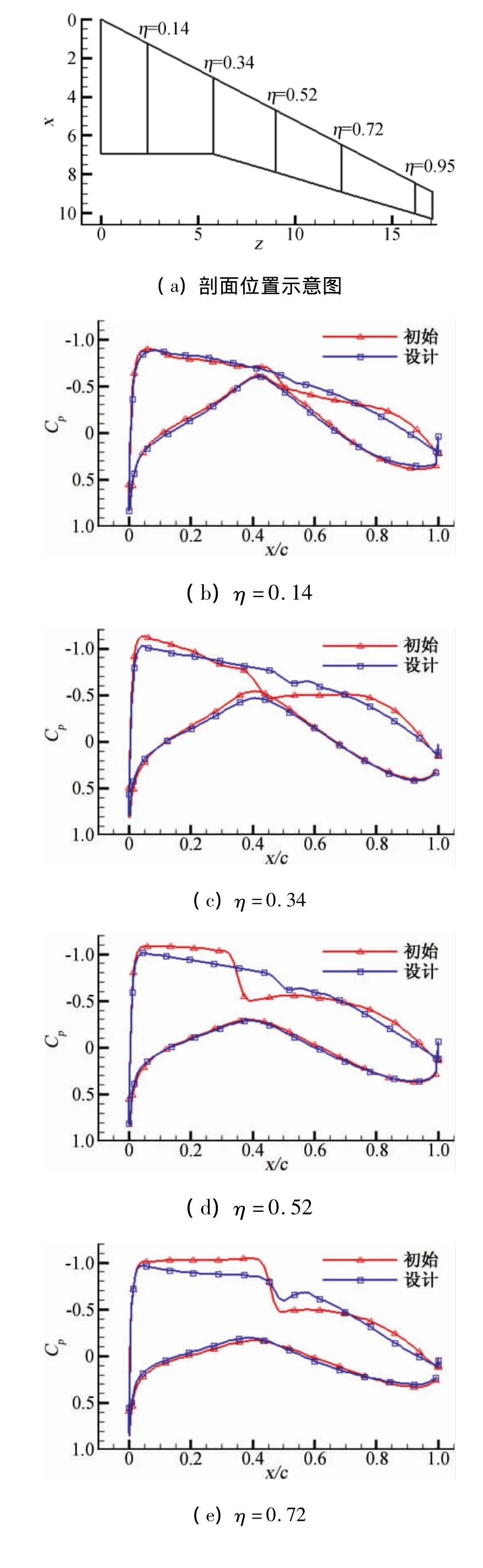
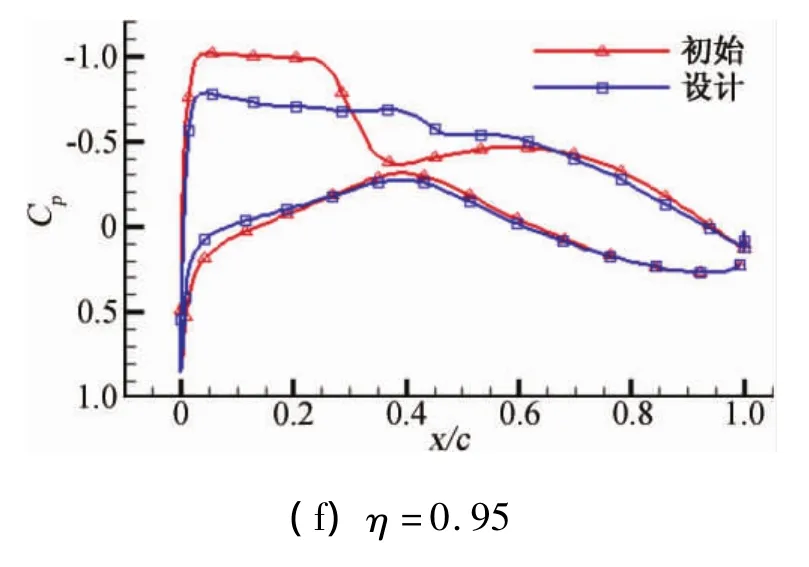
图6 剖面压力系数Fig.6 Section pressure distributions

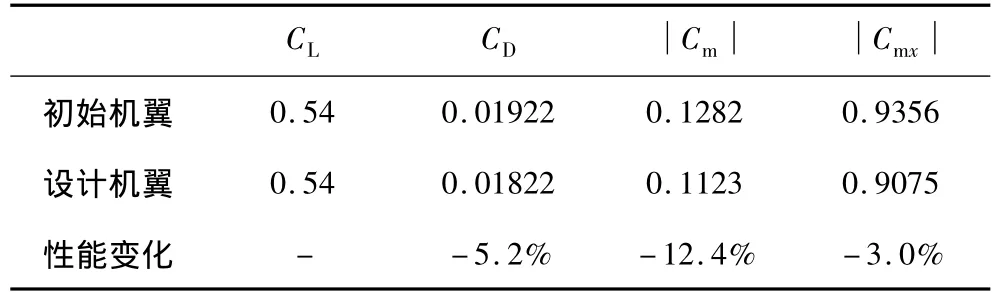
表1 机翼优化结果Table 1 Wing optimization results

整个优化过程在单台PC机上完成，耗时约6天，如果采用大型计算机进行并行和分布式计算，将可能在数小时之内完成一次优化，使设计周期显著降低。

3 结论

采用改进的量子粒子群MQPSO优化Kriging模型的相关模型参数可显著提高代理模型预测精度，与具有双层结构的量子粒子群算法KMQPSO相结合，实现对每个参与CFD计算的粒子进行精准更新。高维度的跨声速机翼优化算例表明该方法稳定高效，设计结果理想，可大幅度提高随机算法在三维气动外形优化中的工程实用性。

［1］JAMESON A.Aerodynamic-structural design studies of lowsweep transonic wings［R］.AIAA 2008-145，2008.

［2］MORRIS A M，ALLEN C B，RENDALL T C S.Aerodynamic optimisation of modern transport wing using efficient variable fidelity shape parameterisation［R］.AIAA 2009-1277.

［3］左英桃，高正红，夏露.基于Euler方程和离散共轭方法的气动外形优化设计［J］.应用力学学报，2009，26(1):22-27.

［4］DUVIGNEAU R，VISONNEAU M.Hybrid genetic algorithms and neural networks for fast CFD-based design［R］.AIAA 2002-5465，2002.

［5］KHURANA M S，WINARTO H，SINHA A K.Airfoil optimisation by swarm algorithm with mutation and artificial neural networks［R］.AIAA 2009-1278，2009.

［6］任庆祝，宋文萍.基于Kriging模型的翼型多目标气动优化设计研究［J］.航空计算技术，2009，39(3):77-82.

［7］SUN J，FENG B，XU W B.Particle swarm optimization with particles having quantum behavior［A］.Proc of the IEEE Congress on Evolutionary Computation［C］，2004:325-331.

［8］KENNEDY J，EBERHART R C.Particle swarm optimization［A］.Proceedings of IEEE International Conference on Neural Networks Perth［C］.Australia，1995:1942-1948.

［9］孔庆琴，孙俊，须文波.基于QPSO的改进算法［J］.计算机工程与应用，2007，43(28):58-60.

［10］CRESSIE N A C.Statistics for spatial data［M］.New York:John Wiley ＆ Sons，1993.

［11］LOPHAVEN S N，NIELSEN H B，SNDERGAARD J.DACE:a matlab kriging toolbox［R］.Technical Report MM-TR-2002-12.Denmark:Technical University of Denmark，2002.

［12］游海龙，贾新章.基于遗传算法的Kriging模型构造与优化［J］.计算机辅助设计与图形学学报，2007，19(1):64-68.

［13］陈鹏，李剑，管涛.基于PSO的Kriging相关模型参数优化［J］.微电子学与计算机，2009，26(4):178-181.

［14］于向军，张利辉，李春然，等.克里金模型及其在全局优化设计中的应用［J］.中国工程机械学报，2006，4(3):259-261.

［15］LONG T，LIU L，WANG J B，et al.Multi-objective multidisciplinary optimization of long-endurance UAV wing using surrogate model in Model Center［R］.AIAA 2008-5918.

［16］RAJAGOPAL S，GANGULI R.Multidisciplinary design optimization of an UAV wing using kriging based multi-objective genetic algorithm［R］.AIAA 2009-2219，2009.

［17］HICKS R M，HENNE P A.Wing design by numerical optimization［J］.Journal of Aircraft，1978，15(7):407-413.

［18］《飞机设计手册》总编委会.民用飞机总体设计［M］.北京:航空工业出版社，2005:58-59.