基于有限体积格式的自适应笛卡尔网格虚拟单元方法及其应用
胡 偶,赵 宁,刘剑明,王东红
(南京航空航天大学航空宇航学院,江苏南京 210016)
0 引言
众所周知,计算流体力学中一个持续的障碍是复杂几何外形的网格生成。自适应笛卡尔网格作为一种新兴的网格生成方法具有结构网格和非结构网格方法所无法比拟的优势。自适应笛卡尔网格生成简单,省时,同时网格结构简单,易于实现自动化、具有更强的自适应能力,可提高计算精度。尤其对于复杂几何外形问题,如果使用传统的结构网格,通常使用嵌套网格和多块对接网格等,虽然这些方法已经得到了成功的使用,但它们需要交换不同网格间的数据信息,会遇到一些复杂的插值和几何的问题;非结构网格虽然易于生成复杂外形的网格,但非结构网格生成费时,计算时间存储量一般都比结构网格高;而使用自适应笛卡尔网格则可以避免这些问题,使得网格生成变成一个简单而省时的过程。
对于复杂几何外形的物体,使用笛卡尔网格方法,在物面边界处网格单元必然与物面相交,从而产生不同形状的切割网格单元。切割网格单元存在的一个普遍问题就是在切割的过程中会产生非常小的切割单元,这就导致了方程系统的刚性以及在物面处会产生解的非物理振荡。并且对于时间依赖问题的数值模拟,会限制时间步长且影响稳定性。为了克服上述问题,很多学者给出了多种处理方法,主要有混合网格方法(hybrid grid)[1],融合单元方法(merged cell approach)[2],嵌入单元方法(embedded cell method)[3],以及虚拟单元方法(ghost-cell method)[4]或浸入边界方法(immersed boundary method)[5]等。
自适应笛卡尔网格与虚拟单元方法结合处理复杂物面边界是一个新的发展方向。最近,Dadone和Grossman 在他们的一系列文章[6,7,8]中,系统研究了结构网格中的虚拟单元方法,并把他们命名为CCST(Curvature Corrected Symmetry Technique)方法,而且这些有效的边界处理方法也被他们推广用于笛卡尔网格[9,10,11],并取名为GBCM方法。本文基于有限体积格式,将虚拟单元方法与自适应笛卡尔网格结合,采用了按边扫描的有限体积方法。此种方法不同于通常的叉树结构的自适应笛卡尔网格方法,虽然增加了计算存储量,但计算效率更高。同时,由于采用了有限体积方法而不是通常的有限差分方法,能更好地满足守恒性要求。此外,本文利用基于速度的散度和旋度的判据,对流场进行解的自适应,能够更为准确地捕捉激波等流动特征,数值结果显示本文所使用的自适应方法具有很好的分辨率,且易于实现。
1 控制方程与数值方法
采用自适应笛卡尔网格最突出的问题就是在不同层次的网格过渡区会出现悬挂节点情况,这对代码的编制以及数值模拟的精度都有很大的影响。本文采用一种基于自适应笛卡儿网格的有限体积方法,将这些带有悬挂节点的网格边当作两条边来处理,从而有效地解决了悬挂节点问题。
二维Euler方程的积分守恒型的表达式如下:
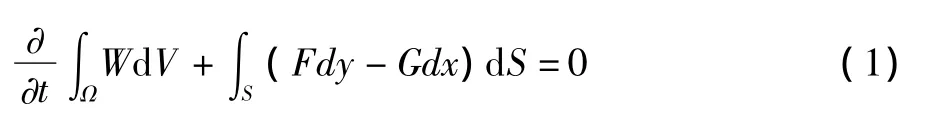
式中W为守恒变量,F,G分别为笛卡尔坐标系下的x,y方向的通量。基于有限体积格式的流动求解器主要包括以下几个方面的内容:解的重构,Riemann求解器,时间方向离散等。
对于有限体积格式,解的重构主要有两种方法:Green-Gauss方法和最小二乘方法。由于本文所采用的是自适应笛卡尔网格,网格的结构相对简单,但又存在不同层次网格过渡的问题,过渡区网格结构不一致,同时本文采用的叉树网格数据结构能够十分便捷地给出网格单元的邻居的信息,因此本文采用了最小二乘法进行解的重构,具体表达形式参见文献[12,13]。
本文采用的Riemann求解器是由Liou和Steffen提出来AUSM格式[14],AUSM格式具有结构简单,对激波具有很好的捕捉等特性。时间方向离散采用四步Runge-Kutta显示时间推进方法。
同时,针对本文所采用的自适应笛卡尔网格,由于网格的非贴体性,需要采用特殊的方法来处理物体壁面边界,给出合适的壁面边界条件,本文采用一种称作虚拟单元方法的浸入边界处理方法。
2 虚拟单元方法
采用笛卡尔网格,物体与网格相交,如图1所示。图中圆圈和三角形表示物体内部的网格点,即虚拟单元(Ghost Cells);实心正方形表示虚拟单元点关于物面边界的对称点。本文使用虚拟单元方法需要给出浸入边界(Immersed Boundary)内部网格点处的物理量,例如点A处的值。
在文献[6]中,Dadone等人针对贴体结构网格提出了一种新的边界条件处理方法,并命名为CCST方法(Curvature-Corrected Symmetry Technique)。虚拟单元点上的流场值是通过在物面附近假设的一个法向具有局部对称分布的熵(S)与总焓(H)的涡流场得到的。这种流动模型满足如下的法向动量方程:
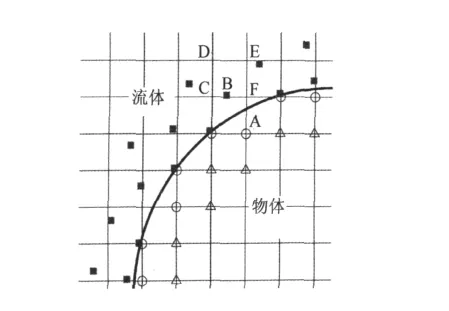
图1 笛卡尔网格Fig.1 Cartesian grid

其中R是带符号的局部曲率半径,如果曲率中心在物体内部为正,反之为负;是切向速度,满足无穿透边界条件·=0。由于沿着物体的表面法向强加反对称的熵与总焓的法向导数 ∂S/∂n,∂H/∂n。这种熵与总焓分布使得在无旋流动时,熵与总焓的法向导数为零,甚至在物面出现涡时也能满足Crocco关系。对于二维问题,为了求虚拟单元点A的流场值,给出了如下的表达式:

上式中B点为虚拟单元点A关于物面的法向对称点。Dadone在文章中比较了GBCM方法与贴体网格下的CCST方法,得出GBCM方法与贴体网格下的CCST方法具有相同的优越性。
在数值计算中虚拟单元中心A所对应的法向对称点B变量的值可以通过一般插值得到,例如图1中的B点,我们可以通过其周围的四个流场网格点C、D、E、F采用双线性插值[5,6]方法(三维使用三线性插值[7])得到,而对于那种不能找到四个流场网格点的情况,我们可以采用逆距离插值方法,这样在我们的代码中就能保证始终使用流体内部网格点来插值。
3 解自适应
为了能够自动地捕捉流场特征,有必要针对流场解

4 数值验证与应用
为验证本文基于有限体积格式的自适应笛卡尔网格虚拟单元方法的有效性,本文分别以NACA0012翼型和RAE2822翼型绕流问题为例,进行了数值模拟,最后采用本文的方法对双错位NACA0012翼型进行了数值模拟。
4.1 NACA0012翼型的守恒性验证
本文以NACA0012翼型绕流为例来比较基于有限体积格式的自适应笛卡尔网格方法相对于传统的基于有限差分方法的自适应笛卡尔网格的差别。来流马赫数 M∞=0.8,攻角 α =0.0°,计算网格如图 2(a)所示,网格进行了7次局部加密,在计算的过程中网格不进行解自适应,以避免网格的不同影响计算结果的比较。翼型的表面压强系数分布如图2(b)所示,从图中我们可以看出,使用传统的有限差分方法激波位置明显偏离正确的位置,所以为了克服守恒性问题,Berger[16]等人提出需要在粗细网格界面处对粗网格单元作守恒修正,使得流入到细网格的通量等于从粗网格流出的通量,但这个过程增加了计算复杂度,而使用本文的有限体积方法,守恒性能很好地满足,激波位置与参考文献[17]的结果吻合的很好。
4.2 RAE2822翼型解自适应验证

考虑来流马赫数 M∞=0.75及攻角 α=3.19°的RAE2822翼型绕流。在这种状态下,翼型的上表面会形成一道强激波。在计算的过程中我们进行了三次解自适应加密,三次解自适应粗化,最终得到的计算网格如图3(a)所示,计算网格的总数为10320个。图3(b)和图3(c)分别给出了压强云图和翼型表面的压强系数分布。从图中可以看出,压力值在网格变化区域过渡光滑,激波位置捕捉精确,与参考文献[18]中的结果吻合的比较好。
4.3 双错位NACA0012翼型
以双错位NACA0012翼型为例,验证本文方法对多物体计算的有效性。其中来流马赫数M∞=0.70,攻角α=0.0°。在该算例中,两个翼型之间会形成一道强激波,类似于管道流动。在计算的过程中本文进行了三次解自适应,最终的计算网格图如图4(a)所示,网格总数为16337个。图4(b)和4(c)分别给出了压强云图和上下两个翼型表面的压强系数分布,从图中可以看出,激波结构清晰,位置准确,与参考文献[18]中的结果吻合的比较好。

5 结论
本文发展了基于有限体积格式的自适应笛卡尔网格虚拟单元方法,并成功地将这种方法应用于不同流动问题,并使用本文的方法成功地进行多物体流动问题的求解,得到了理想的结果。数值实验显示本文方法是十分有效的,为将这些方法推广并应用到三维问题奠定了良好的基础。

[1]CHARLTON E F.An otree solution to conservation-laws over arbitrary regions(OSCAE)with applications to aircraft aerodynamics[D].[Ph.D.Thesis].University of Michigan,1997.
[2]UDAYKUMAR H S.Multiphase dynamics in arbitrary geometries on fixed cartesian grids[J].Journal of Computational Physics,1997,137:366 -405.
[3]MARSHALL D D.Extending the functionalities of cartesian grid solvers:viscous effects modeling and MPI parallelization[D].Ph.D.Thesis,Georgia Institute of Technology,2002.
[4]DADONE A and GROSSMAN B.An immersed body methodology for inviscid flows on cartesian grids[R].AIAA Paper,2002 -1059,2002.
[5]FORRER H,JELTSCH R.A higher order boundary treatment for cartesian-grid method[J].Journal of Computational Physics,1998,140(2):259 -277.
[6]DADONE A,GROSSMAN B.Surface boundary conditions for the numerical solution of the Euler equations[R].AIAA 93-3334.1993.
[7]DADONE A.Symmetry technique for the numerical solution of the 2d Euler equations at impermeable boundaries[J].Int.J.Numer.Meth.Fluids.,1998,28(7):1093 -1108.
[8]DADONE A,GROSSMAN B.Surface boundary conditions for the numerical solution of the Euler equations in three dimensions[J].Lect.Notes.Phys.,1995,453:188 -94.
[9]DADONE A,GROSSMAN B.Ghost-cell method for inviscid two-dimensional flows on cartesian grids[J].AIAA JOURNAL,2004,42(12):2499 -2507.
[10]DADONE A,GROSSMAN B.Ghost-cell method with far field coarsening and mesh adaptation for Cartesian grids[J].Computers& Fluids 2006,35(7):676-687.
[11]DADONE A,GROSSMAN B.Ghost-cell method for inviscid three-dimensional flows on cartesian grids[J].Computers &Fluids,2007,36(10):1513 -1528.
[12]WANG Z J.A quadtree-based adaptive Cartesian/quad grid flow solver for Navier-Stokes equations[J].Computers &Fluids,1998,27(4):529 -549.
[13]VENKATAKRISHNAN V.On the accuracy of limiters and convergence to steady state solutions[R].AIAA Paper 93 -0880,1993.
[14]LIOU M S,STEFFEN C J.A new flux splitting scheme[J].J.Computional Physics,1993,107:23 -39.
[15]DARREN L.DE ZEEUW.A quadtree-based adaptively-refined Cartesian-grid algorithm for solution of the Euler equations[D].[PhD thesis].The University of Michigan,1993.
[16]BERGER M J.Local adaptive mesh refinement for shock hydrodynamics[J].J.Comput.Phys.,1989,82:64 -84.
[17]STOLCIS L,JOHNSTON L J.Solution of the Euler equations on unstructured grids for two-dimensional compressible flow[J].Aeronautical Journal,1990,94:181 -195.
[18]马志华.自适应无网格及网格和无网格混合算法研究[D].[博士学位论文].南京:南京航空航天大学,2008.

