基于BP神经网络考查课评分系统

吉淑娇，牟敦海

(1.长春大学 电子信息工程学院，长春 130022;2.珲春金山矿业有限公司，吉林 珲春 133300)

基于BP神经网络考查课评分系统

吉淑娇1，牟敦海2

(1.长春大学 电子信息工程学院，长春 130022;2.珲春金山矿业有限公司，吉林 珲春 133300)

考查课在大学课程中占有很大的比例，而其成绩的评定易受教师主观因素影响，不够准确。利用具有自学习、自识别能力的BP神经网络建立考查课考评体系，不断调整网络的权值使SSE(平方误差和)总朝着减小的方向发展，直到达到目标误差为止。

BP神经网络;考查课;评分系统

0 引言

大学的课程里，考试课和考查课各占一部分，近年来考查课的比例明显增多，而对考查课的成绩评定学校鼓励老师采取灵活多样的考核方式，如开卷考试，口试或论文等。但是这些评分方法都不够准确、全面和系统，容易出现主观性。如果成绩评分不准确、不科学，将对学生获得奖学金和各种奖励都有影响。因此，探求一种能尽量排除各种主、客观因素的干扰和影响，使其科学、实际的测评方法是十分必要的［1］。

BP神经网络是基于误差反向传播算法的多层前向神经网络，BP算法目前已成为应用最为广泛的人工神经网络学习算法，可以实现输入和输出之间的任意非线性映射。本文以和考查课有关的几方面因素的分值作为BP神经网络的输入，通过神经网络运算来模拟一个合理的评分系统，以成绩是优秀、良好、中等、及格或者不及格中的一种作为输出。充分利用BP网络的非线性、泛化和容错能力，不算调整网络的权值，使其总朝着减小的方向发展，直到达到目标误差为止。

1 标准BP神经网络结构

BP(Back Propagation)神经网络的学习过程采用误差反向传播算法，是一个有导师的神经元网络学习算法。BP神经网络由输入层、中间层、输出层组成的阶层型神经网络，中间层可扩展为多层。其各个层次之间的神经元相互连接，同一层内的各个神经元互不连接，且建立在梯度算法的基础之上。网络按有教师示教的方式进行学习。当一对学习模式提供给网络后，将输入模式经网络输人层、隐层、输出层逐层的处理之后得到一个输出模式。计算网络输出模式和期望输出模式的误差，将误差由输出层、隐层、输入层的反向顺序传送。按照减小误差的方向逐层修正各层连接权重，当误差小于事先规定值时，整个学习过程就会结束。图1基本的BP网络结构［2－3］。

这种网络结构对于输入信息，要先向前传播到隐含层的节点上，经过各单元的特性为Sigmoid型的激活函数运算后，把隐含节点的输出信息传播到输出节点，最后给出输出结果。［x1，x2，…xi…xn］分别代表BP神经网络的输入信号，［wj1…wji…wjn］则代表前一神经元与后一神经元的链接强度，即权值。f(·)表示转移函数，通过转移函数确定其输出。

图1 基本的BP网络结构

2 BP神经网络算法建模

BP网络的训练算法是典型的有监督训练算法，它的基本思想是把一组样本的输入输出问题变为一个非线性优化问题，用优化中普遍使用的梯度下降法来实现网络的实际输出和期望输出相逼近BP神经网络的建模包括BP神经网络的构建、BP神经网络训练和BP神经网络分类三步，算法流程如图2所示。

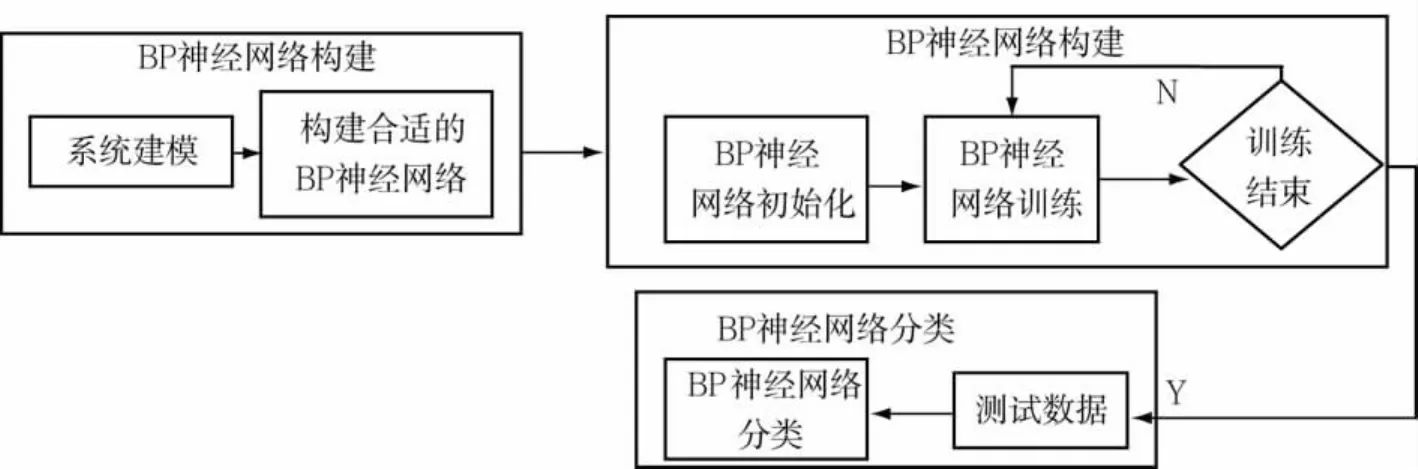
图2 BP神经网络的算法流程

3 BP神经网络在考查课评分体系中的应用

3.1 评价模型的建立

学生的考查课的成绩评定主要以学生的平时出勤次数、交作业次数、课堂回答问题、课堂纪律以及实验成绩和论文成绩来综合决定。本文采用如下的评价方案，由这6项指标的成绩向量作为BP网络的输入。因为输入各个分量数值的数量级有很大的差异，因此需要对输入数据进行归一化处理，使数据都在［0，1］范围内。本文采用最大最小值法，因为该方法对数据的处理是一种线性的变换，能够较好地保留其原始的意义，不会造成信息的丢失。常用下面的公式1来变换。

输出神经元的个数确定可以根据各个学校和教师给定成绩的特点及类别来得到。一般成绩级别为5分制，可将输出神经元个数定为3个，并确定其不同组合100、010、011、100和101分别代表5种成绩，即:优、良、中、及格、不及格;至于隐含层神经元的个数的确定，则是根据经验以及实验测试情况不断调整。表1为取的15个同学的归一化处理数据作为样本，其中10个同学的数据作为训练数据，5个同学的数据作为测试数据。

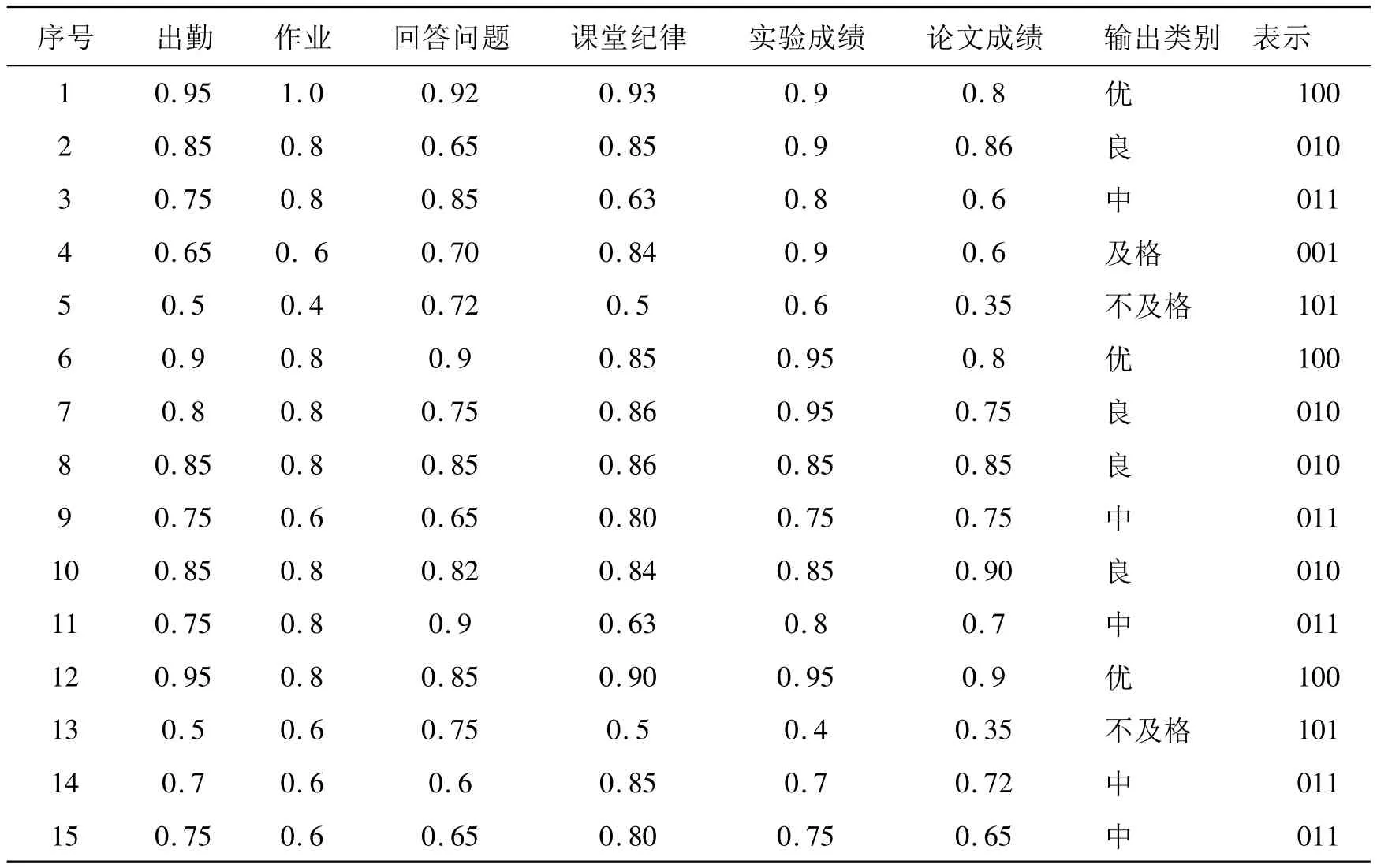
表1 归一化的学习样本和测试数据

3.2 MATLAB 实现

利用Matlab7.1编程建立3.1中的三层BP神经网络。网络的每一层激活函数均采用单级S型函数，即:

具体训练步骤如下［4－5］:

(1)确定神经网络的结构参数:定义输入、隐含和输出层的神经元的个数，定义网络收敛误差，选取合适的动量常数和学习效率，训练样本数;

(2)输入层样本的值为决定四个因素的指标值构成，期望输出为值;

(3)网络权值随机初始化;

(4)从前向后计算各层隐含和输出层单元;

(5)计算输出层的误差信号;

(6)从后向前计算隐含层的误差信号;

(7)计算并保存各权值修正量;

(8)计算误差，如果误差小于定义的收敛误差停止训练;否则重复步骤4直至收敛。

本系统中，隐层传递函数使用“tansig”函数实现，输出层传递函数采用“purelin’存线性函数函数实现。目标训练SSE为0.01，最大训练次数为1000次，动量系数为0.95，初始学习率为0.03，学习率增长系数为1.04，减小系数为 0.75。

训练误差随训练次数的变化情况如图3所示，神经网络经过880 Epochs迭代后达到精度要求。训练的误差平方和SSE曲线如图3左边曲线所示，右边曲线为系统测试的误差平方和SSE，可以看出训练误差与测试误差基本一致。

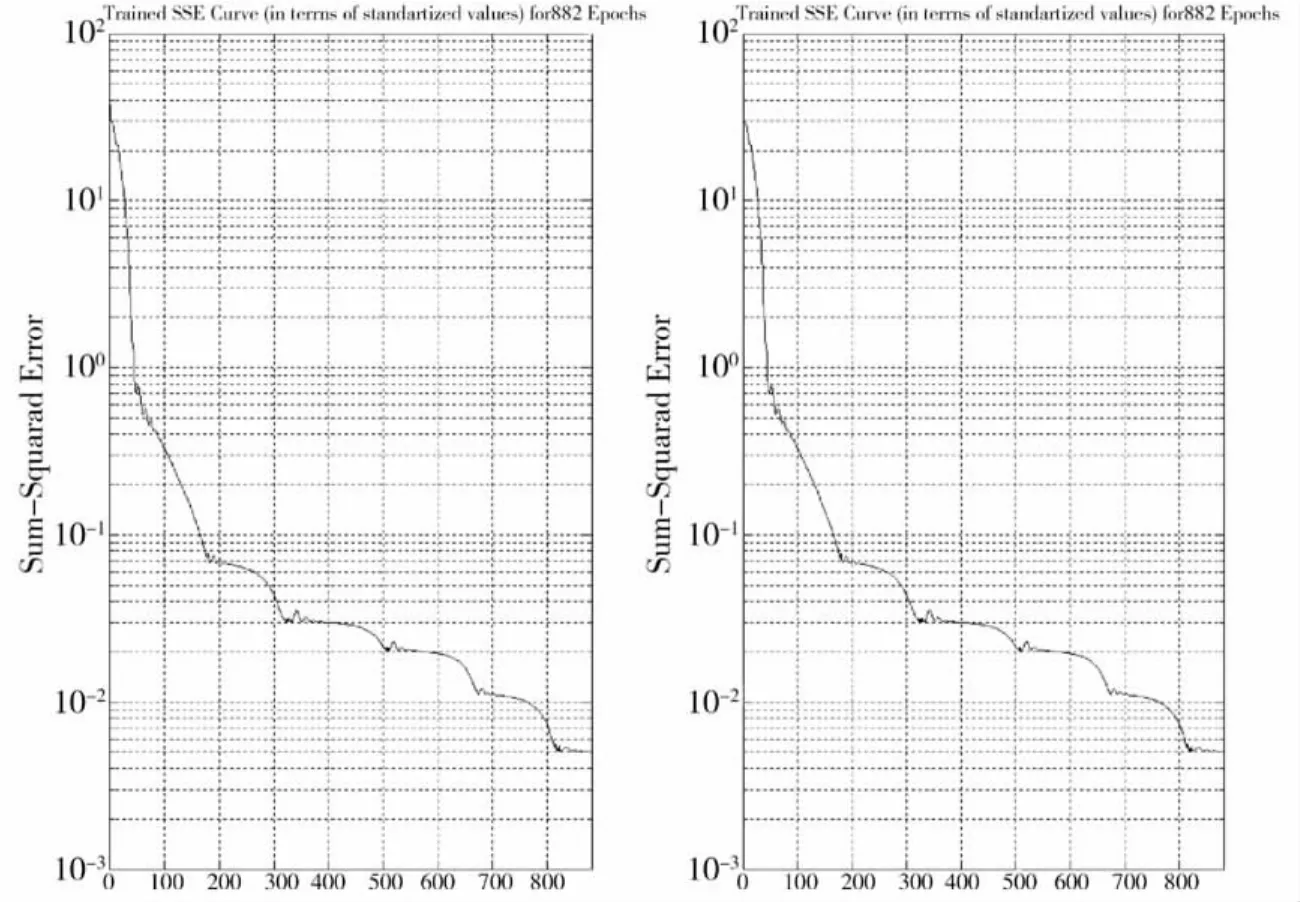
图3 仿真曲线

4 结语

学校鼓励老师对考查课的成绩评定采取灵活多样的考核方式，因此教师在给考查课评分过程中容易出现评价指标对不同学生权重不一致的不稳定情况。由于BP神经网络能够很好的模拟非线性的系统，且具有很好的容错和泛化能力，将其用于考查课评分系统中，使考查课的成绩给定更具合理性和科学性。实验仿真表明，网络训练过程和测试过程经相近的Epoch达到目标误差。

［1］梁飞鸿.BP神经网络在教学质量评价中的应用［J］.电脑与电信，2010(7):55－56.

［2］袁剑.BP神经网络在学生综合考评中的应用［J］.福建电脑，2010(6):91－92.

［3］王文成.人工神经网络及其在汽车工程中的应用［M］.北京:北京理工大学出版社，1998.

［4］冯必波，BP神经网络在教学质量评价体系中的应用［J］.计算机与数学工程，2010(4):97－99.

［5］汪旭晖，黄飞华.基于BP神经网络的教学质量评价模型及应用［J］.清华大学教育研究，2007(1):78－81.

责任编辑:吴旭云

Application of marking system for checking courses based on BP neural network

JI Shu-jiao1，MU Dun-hai2
(1.College of Electronic Information Engineering，Changchun University，Changchun 130022，China;2.Jinshan Mineral Products Co.Ltd.of Hunchun，Hunchun 133300，China)

There are many checking courses in universities.It is susceptible to subjective factors when teachers decide what score a student should have，and the result is not accurate enough.It is necessary to establish a model of checking courses appraisal system by applying BP neural network principle that has the ability of self-learning and self-recognition.We need continuously adjust the network weight to reduce the sum squared error until it reaches the target.

BP neural network;checking course;marking system

TP389.1

A

1009－3907(2011)04－0022－03

2011-01-10

吉淑娇(1979-)，女，吉林长春人，讲师，博士研究生，主要从事信号分析、图像处理方面的研究。