标准镜的高精度柔性支撑镜框的优化设计

王 平，田 伟，王汝冬，王立朋，隋永新，杨怀江

(中国科学院长春光学精密机械与物理研究所，吉林长春130033)

为了实现干涉仪标准镜中光学元件的高精度定位，设计了一种柔性支撑镜框，研究了该结构的力学模型、结构参数、定位精度和透镜变形。首先，根据材料力学原理将柔性镜框等效为一个弹簧系统;根据力学方程和几何关系，建立了透镜中心位置与柔性结构的挠度之间的二元方程。然后，分析了安装位置、温度、结构参数对透镜位置以及作用力的影响。最后，应用有限元仿真分析了所设计结构的力学性能，并进行对比验证。结果表明，数值仿真分析的结果与有限元仿真结果基本相同，柔性镜框的柔性结构厚度最优值为1.5 mm。该设计方案完全满足干涉仪标准镜对镜框在定位精度、稳定性方面的要求。

干涉仪;标准镜;柔性镜框;定位精度;稳定性;有限元分析

1 引言

目前，随着光学仪器精度的提高，对光学元件面形检测的要求越来越高，特别是对光刻机曝光镜头内的光学元件面形的检测，精度需要达到纳米量级。干涉仪是目前用于光学元件面形检测的主要技术手段，利用参考面和待测面之间的干涉条纹测量待测面的面形，其测量精度主要取决于参考面的精度。因此，干涉仪标准具的质量成为制约光学元件检测精度的一个重要因素。用于高精度检测的标准面的面形精度通常要达到纳米级别，这就要求夹持参考镜的镜框具有非常高的定位精度、热稳定性、刚度以及低的应力(甚至无应力)夹持。

常用的透镜夹持方式为镜框加压圈，其结构简单，但是这种方式容易受到环境的影响，温度变化时会产生热应力，并且，压圈压紧时造成的面形变化是高精度标准镜所不允许的。为了保证透镜的高精度面形，工程界提出了很多镜框的结构形式，其中应用最广泛的一种方式就是柔性支撑方式。 王 忠 素［1］、Vukobratovich［2］、Ahmad［3］和Masaki［4］等人都研究了利用柔性结构来支撑光学元件，表明了通过增加镜框结构的柔性可以有效地保证光学元件的面形。同时，透镜高精度夹持的固定方式也主要采用胶粘固定，Vukobratovich［5］和 Christopher［6］等人对光学元件的胶粘固定方式进行了研究。由于上述两种方式的有效性，工程实际中经常将两种方式结合使用。柔性支撑方式是一种利用柔性铰链来降低镜框与透镜之间连接刚度的方式，李琳［7］和单云霄［8］等人对柔性铰链的设计进行了研究，给出了通用柔性铰链的设计公式。干涉测量中环境振动对测量精度影响很大，这要求柔性支撑在保证光学元件面形的同时具有一定的刚度，秦鹏［9］和朱晓明［10］等人对光学仪器的振动特性进行了研究。

在以上研究基础上，本文针对干涉仪标准镜中参考镜镜框的柔性结构进行了优化设计，并讨论了各种环境因素、柔性结构的结构参数、安装方式对透镜的定位精度和作用力的影响。仿真分析结果表明，选择合适的柔性结构形式，可以有效地保证标准镜的位置和面形精度，并且能够保证温度、振动对透镜的位置和面形精度的影响非常小。

2 柔性镜框的结构模型

柔性镜框的结构模型如图1所示，透镜与镜框之间通过3个柔性结构连接。为了实现干涉仪标准镜对透镜之间倾斜和偏心公差的要求，需要通过定心仪检测透镜与镜框之间的对准，在保证两者同轴以后，从柔性结构的注胶孔注入结构胶，将透镜与镜框固定在一起。

图1 柔性支撑镜框结构图Fig.1 Structural diagram of flexure barrel of lens

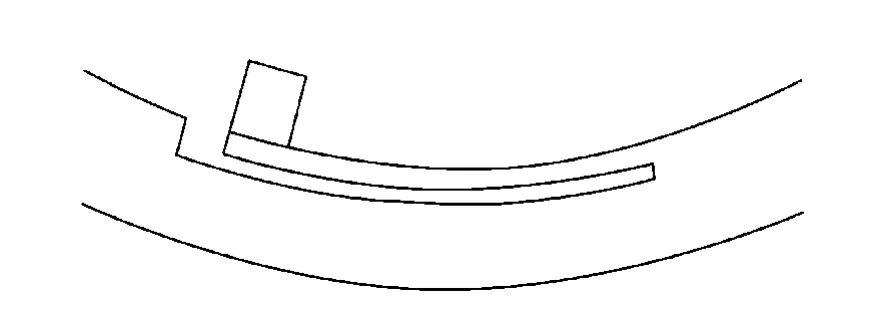
图2 柔性支撑结构示意图Fig.2 Structural diagram of flexure structure

柔性结构是用线切割机床加工出的薄片，如图2所示，其一端与镜框连接，另一端通过胶点与透镜连接。由于线切割机床可以实现微米量级的加工精度，因而，可以保证每个柔性结构都具有相同的几何尺寸和力学性能。当温度发生变化时，这种结构仍然能够保证透镜与镜框同轴，并且在极端的冲击和振动环境下允许透镜偏心，并在这些动态干扰平息之后，使透镜恢复到原来的正确位置。柔性结构可等效成如图3所示的矩形截面的悬臂梁机构。悬臂梁的末端具有6个自由度，但是，由于模型中 t≪b，t≪l，柔性结构在镜框径向方向上的刚度远小于其他方向的刚度。因此，这里假设在外力很小的情况下，只研究悬臂梁的挠度可以近似表征柔性结构的力学特性。

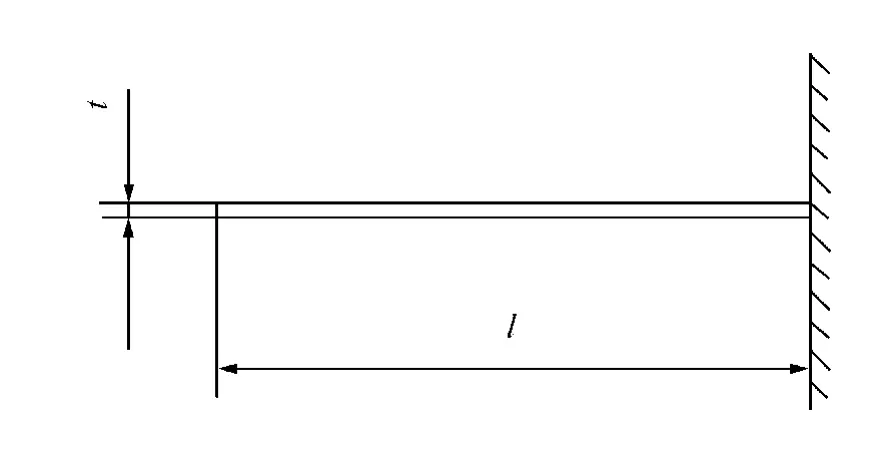
图3 等效悬臂梁示意图Fig.3 Scheme diagram of cantilever model

根据材料力学的理论，悬臂梁在挠度方向上的刚度可以按照下式进行计算：

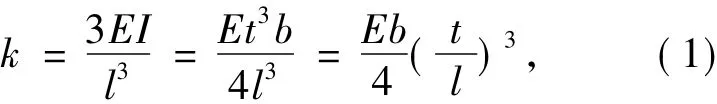
式中：E为材料的弹性模量;I为柔性结构的惯性矩;t为柔性结构的厚度;b为柔性结构的宽度;l为柔性结构的长度。

这样，就可以将柔性支撑镜框的3个柔性支撑结构等效成3个均匀分布的纯弹簧，弹簧的弹性系数为k，其初始长度l=R1-R2，R1为柔性支撑结构在镜框上的基圆半径，R2为镜片的半径。建立透镜与等效弹簧之间的力学模型，如图4所示。由于镜片在装配过程中不能保证其周向位置，因此，力学模型中等效弹簧的布置和重力方向都按照与x轴成一角度布置。

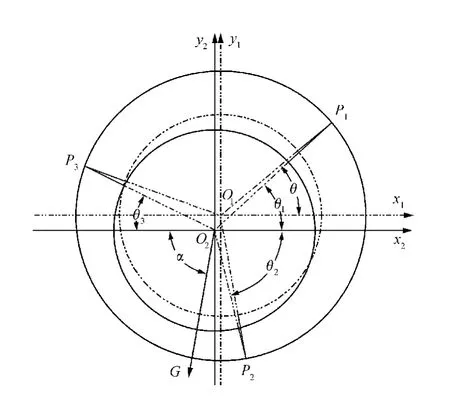
图4 柔性镜框等效力学模型Fig.4 Mechanical model of flexure barrel

图4中内圆为透镜的外径，外圆为镜框的内径，虚线表示透镜在初始状态下的位置，实线表示透镜在重力作用下的位置。透镜从O1移动到O2，发生量偏心量(dx，dy)。在初始状态下，透镜与镜框同心，此时弹簧的长度为镜框内径与透镜外径之差的1/2，3个弹簧成120°均匀布置。由于装配时并不能保证镜框的径向位置，这里假设一个柔性结构与x轴成角度θ。在重力作用下，为了实现力的平衡，各个弹簧要发生一定的形变。

建立力学平衡方程，如下式所示：

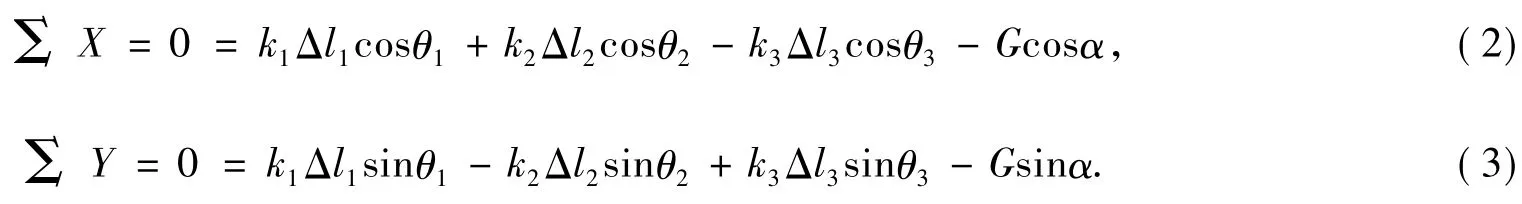
等效模型中，各个弹簧的变形量如下式所示：

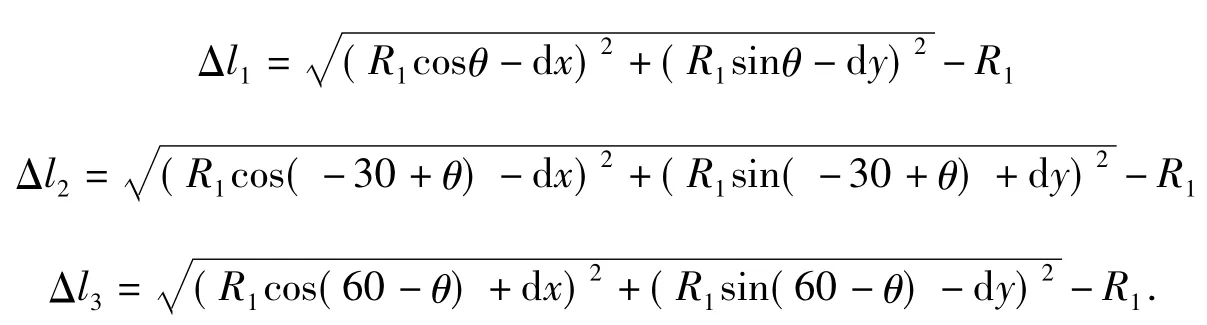
因为柔性镜框与镜子之间具有很高的刚度，因而，重力作用下，弹簧的变形量很小(dx≪R1)，弹簧变形量公式Δl1可以按照下式所示方式化简：

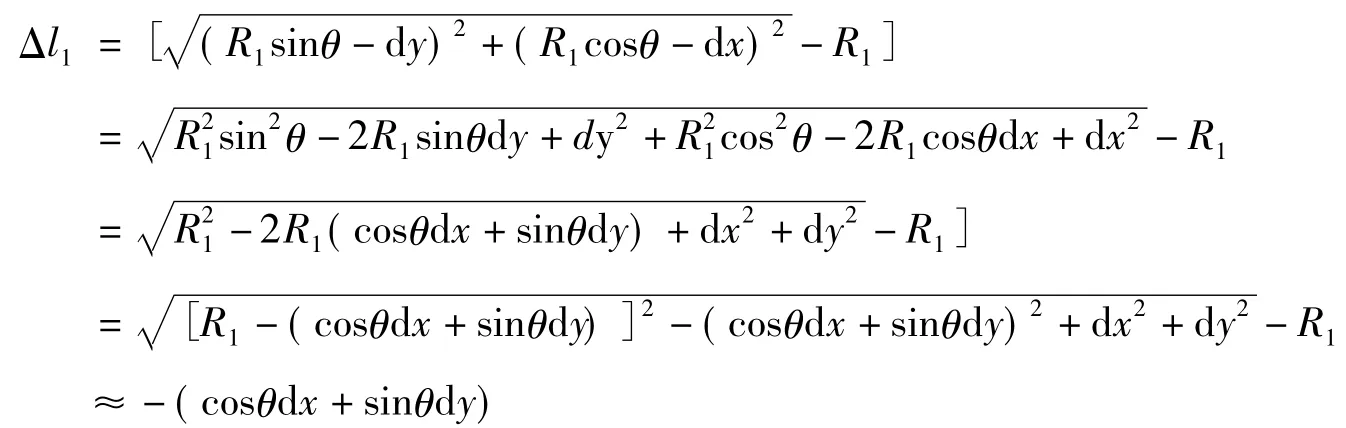
整理公式(2)、(3)。

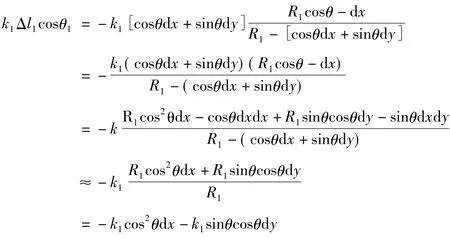
同理，可得：

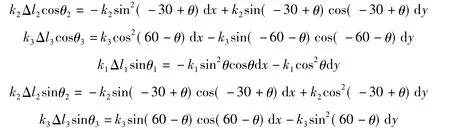
将上述方程带入力学平衡方程，整理可以得 到偏心量(dx，dy)的2元方程组，如下式所示：

其中：

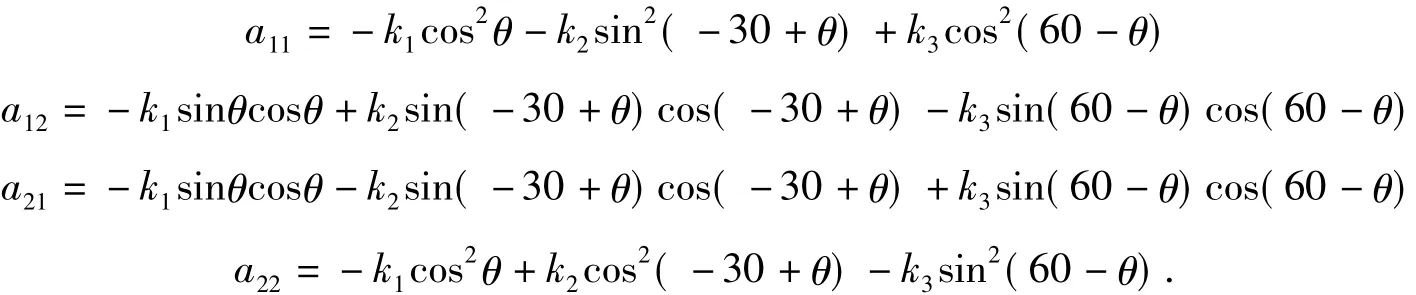
3 柔性镜框的稳定性分析

3.1 结构稳定性

由于镜框的位置是一个装配过程中的随机量，因而重力与柔性结构之间的关系也是一个变化量，需要分析柔性镜框在不同安装状态下对透镜的影响。如图5所示，改变重力的方向(相当于改变透镜的周向位置)，透镜中心的偏心量(dx，dy)不断发生变化。从图6中可以看出，该变化是一个圆形轨迹，也就是说，改变透镜的周向位置，会造成透镜产生一个固定大小的偏心量0.113 μm，这个偏心量指向重力方向。从图7中可以看出，随着周向位置不同，弹簧作用在透镜上的力也是不断变化的，而这种变化的作用力也会使得透镜的面形不断变化，影响干涉仪标准镜的重复性，甚至是光学质量。

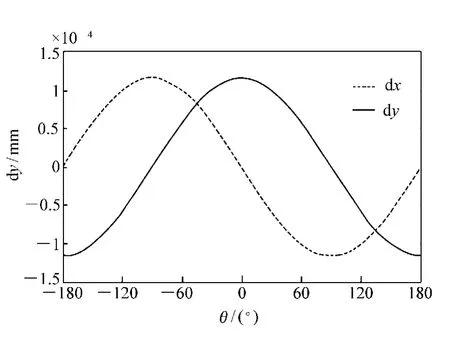
图5 柔性结构位置随重力方向变化的曲线Fig.5 Curve of flexure position changed with gravity direction

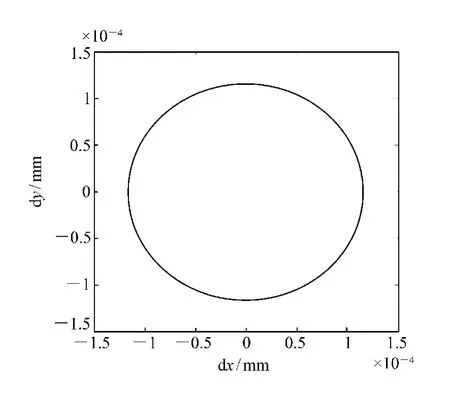
图6 透镜中心的偏心轨迹Fig.6 Partiality contrail of lens center

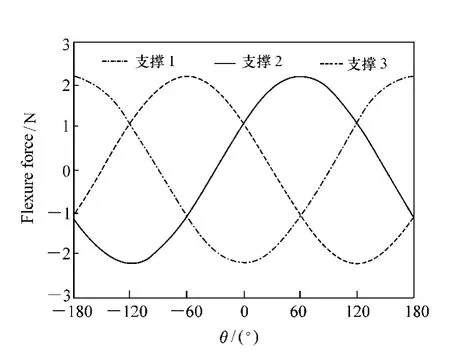
图7 柔性结构随重力方向变化的作用力Fig.7 Curve of flexure force changed with gravity direction

3.2 热稳定性

在受热的情况下，由于透镜与镜框之间的材料差异，会产生一定的相对位置变化。材料的参数如表1所示。假设透镜的热膨胀系数为αG，镜框的热膨胀系数为αM，透镜的半径为R2。那么，当温度变化Δt时，透镜与镜框之间的相对位移量为

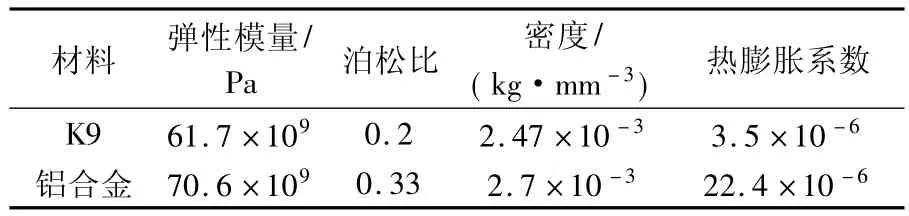
表1 材料性能列表Tab．1 List of materials performance

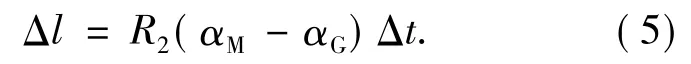
温度变化产生的变形量将作为弹簧的预载施加到各个弹簧上，因此，在温度的影响下，弹簧在重力作用下的变形量如公式(6)所示：

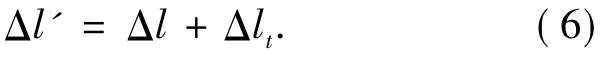
建立力学平衡方程，如公式(7)、(8)所示。可以获得透镜中心在温度变化时的方程组(9)。

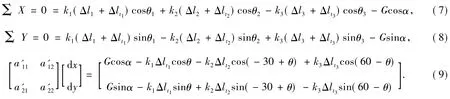
通过仿真分析，镜片的偏心量与温度变化之间的关系如图8所示，从图中可以看出，温度在较大范围内变化时，透镜中心的位置基本不发生变化。也就是说，柔性结构的形变未发生较大的变化，从而作用在透镜上的作用力的变化也很小，能够保证在温度发生变化时，支撑结构对透镜面形的影响非常小。从上述分析可以断定，柔性支撑结构可以保证温度变化时透镜的变形，并保持在装调位置不变。

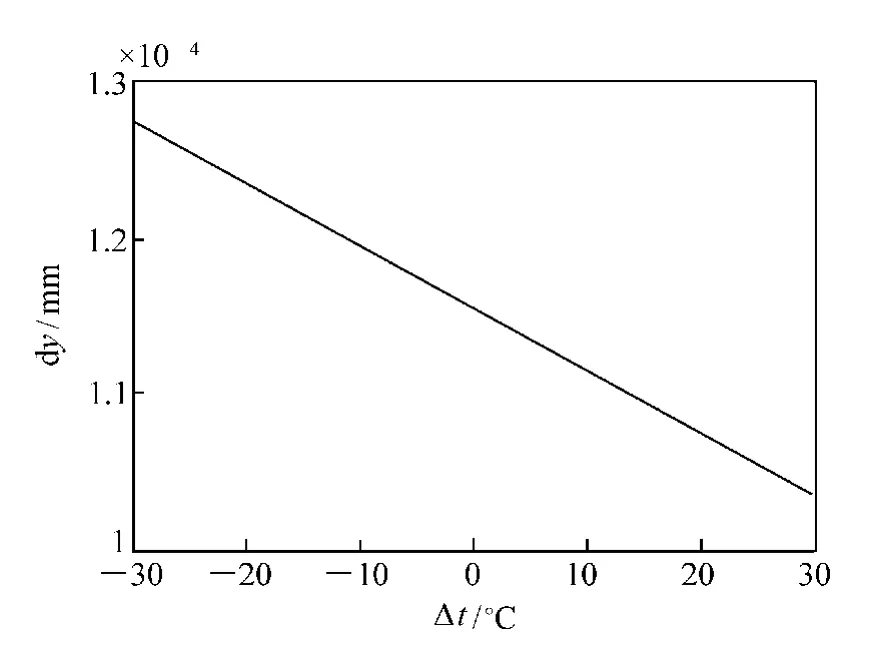
图8 透镜偏心量随温度变化曲线Fig.8 Curve of lens center changed with temperature

4 柔性结构的优化设计

对于一定口径的光学镜片，其镜框的尺寸是确定的，在设计柔性镜框时，柔性结构的长度根据镜框的尺寸进行选择，其长度受加工精度的限制，不能过长，因此，对柔性支撑结构的优化设计主要为选择一个较为合适的柔性支撑结构的厚度量。图9为在温度变化时，不同的柔性结构厚度对弹簧弹力的影响。从图10中可以看出，随着厚度增加，弹簧弹力的增加很快，这会造成镜片面形急剧变坏，并且会产生很严重的应力双折射。随着厚度增加，透镜位置的稳定性也逐渐增加，但是随着厚度的加大，这种改善的效果越来越不明显。

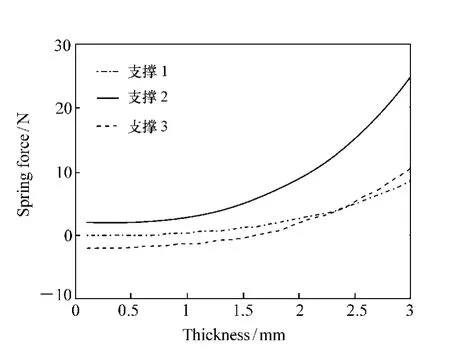
图9 柔性结构弹力随结构厚度变化曲线Fig.9 Curves of spring force of flexure changed with structure thickness

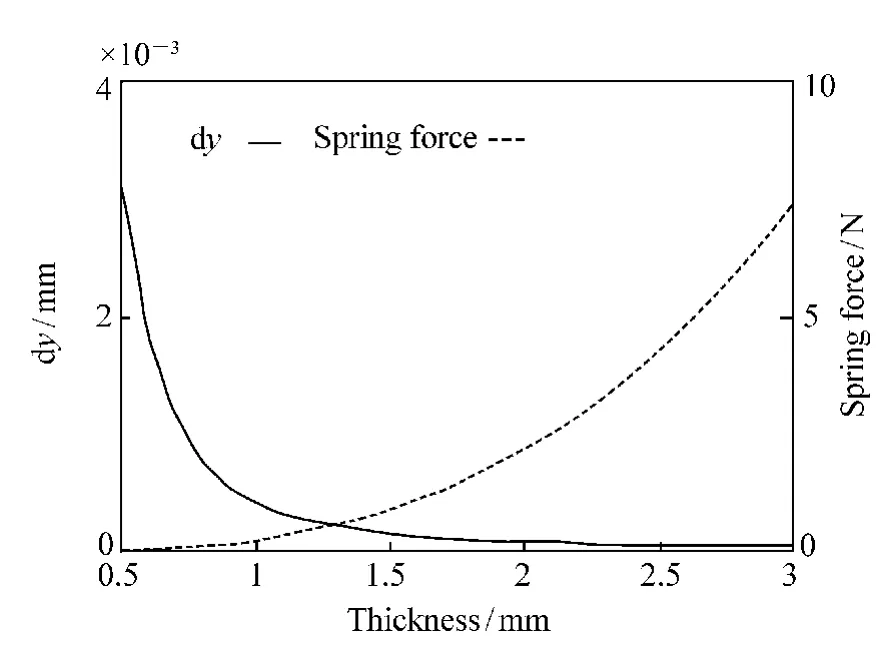
图10 柔性结构弹力和透镜偏心随结构厚度变化曲线Fig.10 Curves of spring force of flexure and lens center changed with structure thickness

为了权衡各种影响因素造成的不利影响，需要选择作用力和偏心量都符合要求的柔性结构厚度。从图10中可以看出，柔性结构厚度为1～2 mm时是较好的尺寸范围，本文综合加工等方面的考虑，将柔性结构的厚度选为1.5 mm。

为了验证上述分析结果是否正确，通过有限元分析的方法对柔性支撑镜框进行验证。应用MSC.Nastran软件进行仿真分析，建立了温度变化0.1℃、重力条件下的仿真模型，柔性结构采用二维壳单元形式，分析结果如图11～14所示。图11为透镜的应力云图，其最大应力为30.3 kPa，发生在下部的两个支撑点附近。图12为透镜的变形云图，其最大变形量为0.114 μm，与数值仿真的结果非常接近。图13为透镜单元的变形云图，可以看出透镜和镜框相对于柔性支撑近似于刚体，在重力作用下整体发生了移动。图14为柔性支撑结构的变形云图，可以看出结构的变形梯度主要沿着长度方向，而在宽度方向上的变形是相等的，这证明了柔性支撑结构在挠度方向上的刚度远小于其他方向的刚度，与数值仿真的假设吻合。

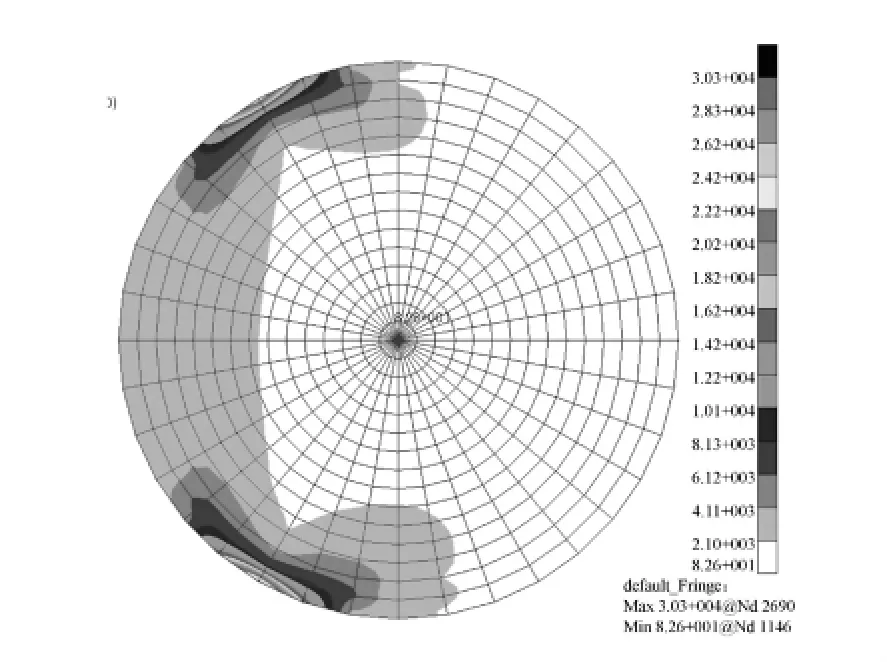
图11 透镜应力云图Fig.11 Nephogram of lens stress

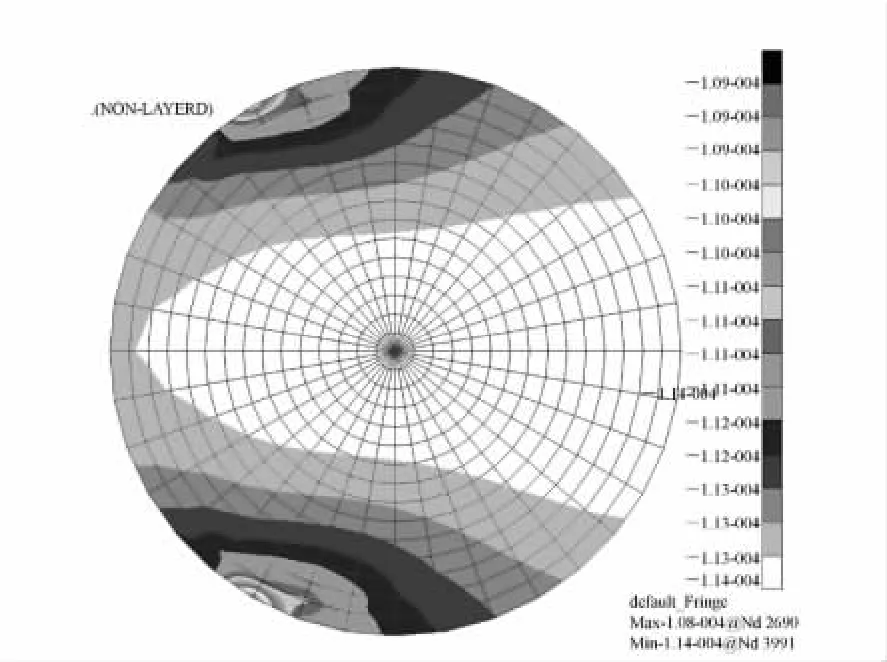
图12 透镜变形云图Fig.12 Nephogram of lens deformation

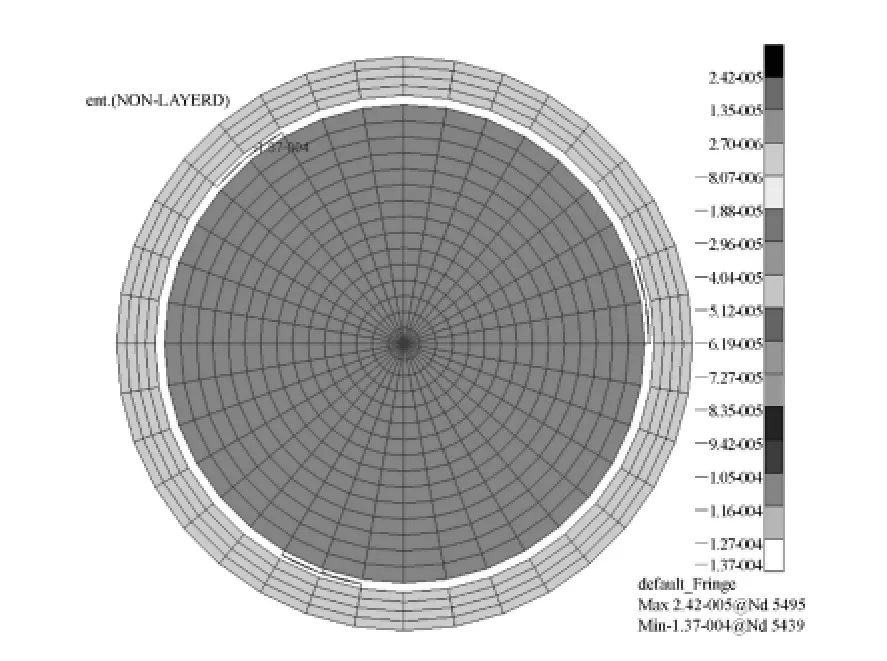
图13 透镜单元变形云图Fig.13 Nephogram of lens unity deformation

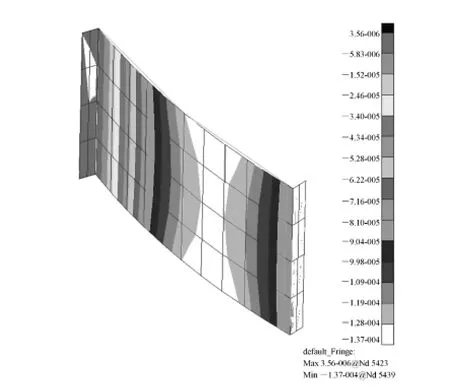
图14 柔性支撑结构变形云图Fig.14 Nephogram of flexure deformation

柔性支撑的一个问题是带来系统刚度的降低，因此，需要分析整个透镜单元的刚度以及其对外界振动冲击的响应。ADAMS/Vibration软件具有非常强大的振动分析功能，本文应用ADAMS/Vibration软件分析整个透镜组件的响应情况，如图15所示。在对光学系统影响较大的低频部分，整个系统都具有很好的隔绝外界冲击的作用。在幅频曲线中，幅值较大的频率为78.73 Hz，为系统的固有频率。从幅频和相频曲线可以看出，整个透镜单元的响应是符合设计要求的。

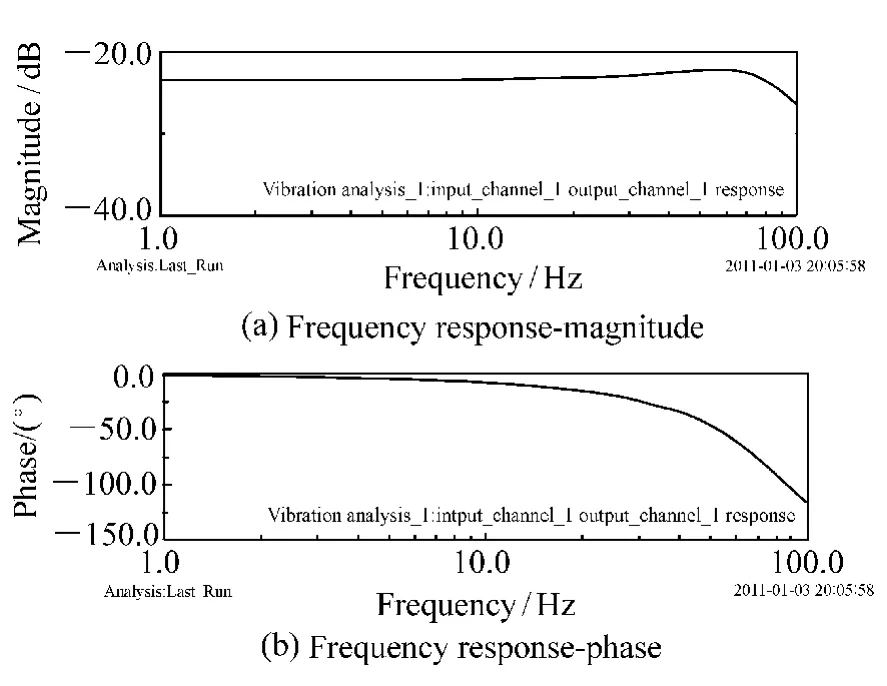
图15 透镜单元响应的幅频和相频曲线Fig.15 Resoponsible curves of lens unity

通过上面的有限元仿真分析结构可以看出，数值仿真的结果与有限元仿真结果基本相同，因此，可以通过数值仿真来优化柔性镜框的柔性结构。本文中的柔性支撑厚度最终设定为1.5 mm，是满足精度要求和加工条件的。

5 结论

设计了一个用于支撑干涉仪标准镜的高精度柔性镜框结构，根据材料力学的理论建立了该柔性结构的仿真模型。通过仿真分析，柔性结构可以很好地提供干涉仪标准镜的高精度定位要求，并且具有较好的稳定性，能够保证透镜在温度变化和外界振动的影响下，光学元件位置稳定。根据柔性结构的厚度对透镜定位精度和作用力的影响，选择了最优的柔性结构厚度为1.5 mm，并通过有限元仿真的方法进行了验证，有限元仿真结果与数值仿真结果非常接近，证明该数值仿真模型切实可行。

［1］ 李琳，杨勇.空间曲线切口式柔性铰链的设计［J］.光学 精密工程，2010，18(10)：2192-2198.LI L，YANG Y.Design of flexure hinges with space curve notches［J］.Opt．Precision Eng．，2010，18(10)：2192-2198.(in Chinese)

［2］ 单云霄，陈长征，刘磊，等.柔性铰链的有限元法设计与分析［J］.中国光学与应用光学，2010，3(2)：146-154.SHAN Y X，CHEN CH ZH，LIU L.design and analysis of flexure hinge by finite element method［J］.Chinese J．Opt．Appl．Opt.，2010，3(2)：146-151.(in Chinese)

［3］ VUKOBRATOVICH D.Flexure mounts for high-resolution optical elements［J］.SPIE，1988，959：18-36.

［4］ VUKOBRATOVICH D，FETTERHOFF K A，MYERS J R，et al..Bonded mounts for small cryogenic optics［J］.SPIE，2000，4131：228-239.

［5］ AHMAD A，HUSE R L.Mounting for high resolution projection lenses：US，4929054［P］.1990-05-29.

［6］ CHRISTOPHER L.Athermal bonded mounts：Incorporating aspect ratio into a closed-form solution［J］.SPIE，2007，6665：666503.

［7］ HOSODA M，PARKS R E，BURGE J H.Vacuum support for a large interferometric reference surface［G］.Tucson：University of Arizona，2010.

［8］ 秦鹏.基于全柔性串接式振动系统的高精度动不平衡测量研究［D］.上海：上海交通大学，2007.QIN P.Research on high accuracy dynamic unbalancing measurement based on fully compliant tandem vibration system［D］.Shanghai：Shanghai Jiao Tong University，2007.(in Chinese)

［9］ 王忠素，翟岩，梅贵，等.空间光学遥感器反射镜柔性支撑的设计［J］.光学 精密工程，2010，18(8)：1833-1841.WANG ZH S，ZHAI Y，MEI G，et al..Design of flexible support structure of reflector in space remote sensor［J］.Opt．Precision Eng.，2010，18(8)：1833-1841.(in Chinese)

［10］ 朱晓明，卢锷.空间光学仪器结构件的动态特性分析及优化［J］.光学 精密工程，1995，3(6)：99-106.ZHU X M，LU E.Dynamical behaviors analysis and optimum design for space optical instrument［J］.Opt．Precision Eng.，1995，3(6)：99-106.(in Chinese)