MRCI方法研究CSe(X1Σ+)自由基的光谱常数和分子常数*

刘慧 施德恒 孙金锋 朱遵略

MRCI方法研究CSe(X1Σ+)自由基的光谱常数和分子常数*

刘慧1)施德恒1)孙金锋2)朱遵略2)

1)(信阳师范学院物理电子工程学院，信阳464000)
2)(河南师范大学物理与信息工程学院，新乡453007)
(2010年8月23日收到;2010年9月18日收到修改稿)

采用内收缩多参考组态相互作用方法在0.08—2.5 nm的核间距范围内计算了CSe(X1Σ+)自由基的势能曲线．为确保势能曲线的计算精度，C原子使用较大的相关一致基aug-cc-pV5Z，Se原子使用最大的相对论赝势基augcc-pV5Z-pp．对CSe(X1Σ+)自由基的势能曲线进行了拟合，并进行了同位素识别，得到了该自由基6个主要同位素分子(12C74Se，12C76Se，12C77Se，12C78Se，12C80Se和12C82Se)的光谱常数De，D0，Re，ωe，ωexe，Be和αe，均与已有的实验结果较为一致．利用CSe(X1Σ+)自由基的势能曲线，通过求解双原子分子核运动的径向Schr dinger方程并进行同位素识别，找到了J=0时该自由基6个主要同位素分子的全部振动态．针对每一同位素分子的每一振动态，还分别计算了其振动能级、经典转折点和惯性转动常数等分子常数．文中的大部分光谱常数和分子常数属首次报道．

同位素识别，势能曲线，光谱常数，分子常数

PACS:31．15．aj，31．30．Gs，31．50．Bc，31．50．Df

1.引言

CSe自由基电子吸收光谱的研究一直备受人们关注，这是因为该自由基对分析高温含Se化合物的性质非常有益［1］．因此，弄清CSe自由基的光谱性质，无论是在理论上还是在实际应用中都有重要意义．

实验方面，许多学者都对CSe自由基的光谱性质进行了研究［2—10］．例如:1935年，Rosen等［2］首次对CSe进行了光谱实验研究;1939年，Barrow［3］由CSe的紫外线光谱导出了其基态的离解能D0;1947年，Ives等［4］改进了CSe光谱源;同年，Howell［5］指出CSe光谱体系1Σ←3Π应类似于CO的光谱体系; 1953年，Laird等［6］对CSe的紫外线光谱进行了研究，分析了其7个波段的转动谱，首次导出了CSe基态的实验光谱常数(平衡核间距Re，谐振频率ωe，非谐频率ωexe，惯性转动常数Be和非惯性转动常数αe);1972年，McGurk等［7］观测到了CSe自由基的7种同位素分子的微波谱，并导出了其Re等光谱参数;1974年，Lovas等［8］利用McGurk等［7］的实验结果拟合出了7种CSe同位素分子的Be和αe;1977年，Radler等［9］利用CSe2的电离谱得到了CSe基态的D0;1999年，Kerr等［10］在其著作中给出了CSe基态的D0等．

理论方面，由于Se原子较大，准确地从头算较为困难，因此关于CSe自由基光谱性质的研究［11—13］较为有限．2001年，Martin等［11］用CCSD(T)方法及相关一致Stuttgart-Dresden-Bonn(SDB)相对论赝势基与核极化势相结合的方法研究了CSe(X1Σ+)自由基的Re，ωe和De;2002年，Kalcher［12］采用CASACPF方法及cc-pVQZ基组计算了该自由基基态的Re，ωe，ωexe和Be;同年，Menconi等［13］用7种交换关联泛函方法及6-311+G(2df)基组计算了45个双原子分子的Re和ωe，其中包括CSe自由基．由于这些计算使用的都是单参考态方法，其光谱常数的计算精度都不是很高．同时，这些文献也未涉及该自由基的振动能级、经典转折点和惯性转动常数等分子常数．

一方面关于CSe自由基的实验研究很多，但对其同位素分子光谱性质的研究却很少;另一方面，也未发现对该自由基同位素分子光谱性质的理论研究．这些激起了我们对该自由基光谱常数和分子常数的研究兴趣．

本文采用内收缩多参考组态相互作用(MRCI)方法［14］，在C原子使用较大的相关一致基aug-ccpV5 Z［15］，Se原子使用最大的相对论赝势基aug-ccpV5 Z-pp［16］的基础上，于0.08—2.5 nm的核间距范围内对CSe(X1Σ+)自由基的势能曲线进行了计算．利用CSe(X1Σ+)自由基的势能曲线，使用MOLCAS程序包［17］提供的VIBROT软件进行同位素识别，拟合出了12C74Se，12C76Se，12C77Se，12C78Se，12C80Se和12C82Se 6个主要同位素分子的光谱常数．通过求解核运动的径向Schr dinger方程并使用同位素识别，找到了J=0时每一主要同位素分子存在的全部振动态．进一步的计算还得到了与每一同位素分子的每一振动态相对应的振动能级，经典转折点和惯性转动常数等分子常数．本文的大部分光谱常数和分子常数均属首次报道，所得到的光谱数据可为进一步的实验或理论研究提供参考．

2.理论方法

单参考态方法研究双原子分子的光谱性质有许多成功的例子［18—21］．但对于较大的双原子分子(如本文的CSe自由基)，要得到准确的势能曲线就必须进行准确的相关能计算，但这是单参考态方法难以做到的，而多参考组态相互作用(MRCI)理论方法就能够实现这一点．

本文关于势能曲线的计算是在MOLPRO2008．1程序包［22］中进行的．CASSCF计算为随后的MRCI计算提供参考波函数．计算过程中为保证势能曲线的精度，C原子使用了较大的相关一致基aug-ccpV5 Z，Se原子则选择了最大的相对论赝势基组augcc-p V5Z-pp．

MOLPRO使用Abelian点群．对于具有简并对称性的分子，则必须使用Abelian子群．也就是说，对于对称性为C∞v的线性分子(如本文的CSe)，计算中必须由C2v群替代，其对应的不可约表示是a1/b1/b2/a2．换句话说，在CASSCF及其后续的MRCI，4．具体地说，在计算CSe(X1Σ+)自由基的势能曲线时，我们将8个分子轨道放入活化空间，这包括4个a1轨道，2个b1轨道及2个b2轨道．这些分子轨道对应于C原子的2s2 p及Se原子的4 s4p壳层电子．其余电子则放入15个闭壳层轨道中(包括8个a1轨道，3个b1轨道，3个b2轨道及1个a2轨道)．这样，参与计算的分子轨道共23个(分别为12个a1轨道，5个b1轨道，5个b2轨道和1个a2轨道)．然而当我们拟合使用这些分子轨道(12 a1，5 b1，5b2和1 a2)计算得到的势能曲线时，得到的光谱数据的精度非常差，这说明得到的势能曲线并不准确．

为获得更准确的势能曲线，需要增大计算过程所使用的活化空间，但较大的活化空间又需要较长的计算时间．为此作者采用逐步增大活化空间的方法来寻找准确计算势能曲线所需的最小活化空间．计算中我们发现，当只增加1个a1轨道，即将9个分子轨道(5个a1轨道，2个b1轨道及2个b2轨道)放入活性空间时即可得到较理想的结果．此时计算所使用的分子轨道为24个，分别是13 a1，5 b1，5b2和1 a2．

势能曲线的计算是在0.08—2.5 nm范围内进行的．在这个范围内，该自由基的势能曲线已完全收敛．计算的步长一般取为0.05 nm，但在平衡位置附近，为能充分展示其势能曲线的特性，计算步长才取为0.01 nm．在整个计算范围内，所得势能曲线既光滑又收敛．

Se原子有多种同位素，其中天然存在的稳定同位素只有6种．这6种同位素的天然丰度分别为0.87%(74Se)，9.36%(76Se)，7.63(77Se)，23.78%(78Se)，49.61%(80Se)和8.73%(82Se)．C原子有3种同位素(12C，13C和14C)，其中12C和13C的天然丰度分别是98.93%和1.07%，14C是放射性同位素，含量非常低，且仅存在于大气的灰尘中．限于篇幅，本文仅计算C原子的主要同位素12C与Se原子的6种稳定同位素形成的同位素分子(12C74Se，12C76Se，12C77Se，12C78Se，12C80Se和12C82Se)的光谱常数和分子常数．

利用CSe(X1Σ+)自由基的势能曲线，通过求解径向Schr dinger方程，作者找到了J=0时6种主要同位素分子的全部振动态．同时，利用MOLCAS 7.4［17］程序包提供的VIBROT软件对CSe自由基进行同位素质质量识别，还计算了12C77Se，12C78Se，12C80Se和12C82Se 6种同位素分子的光谱常数De，Re，ωe，ωexe，αe和Be．

在同位素识别的基础上还利用VIBROT软件进行了各同位素分子相应的振转光谱计算．这里对VIBROT软件计算光谱常数的方法进行简短的说明:VIBROT首先将势能曲线拟合成解析形式．然后，利用Numerov方法［23］对振转Schr dinger方程进行求解，以得到每一同位素分子每一振动态若干转动量子数的振转光谱．通过对振动能级的拟合，即可得到相应同位素分子的光谱常数．

3.结果与讨论

3.1.光谱常数

表1列出了6种同位素分子12C74Se，12C76Se，12C77Se，12C78Se，12C80Se和12C82Se的X1Σ+态光谱常数．为便于比较，表1还列入了已有的实验结果［3，6—10，24］以及其他理论计算结果［11—13］．由于12C80Se同位素分子的天然丰度最高，为便于比较，我们将未进行同位素识别的文献结果［3，6，7，9—13］归入到12C80Se自由基中．

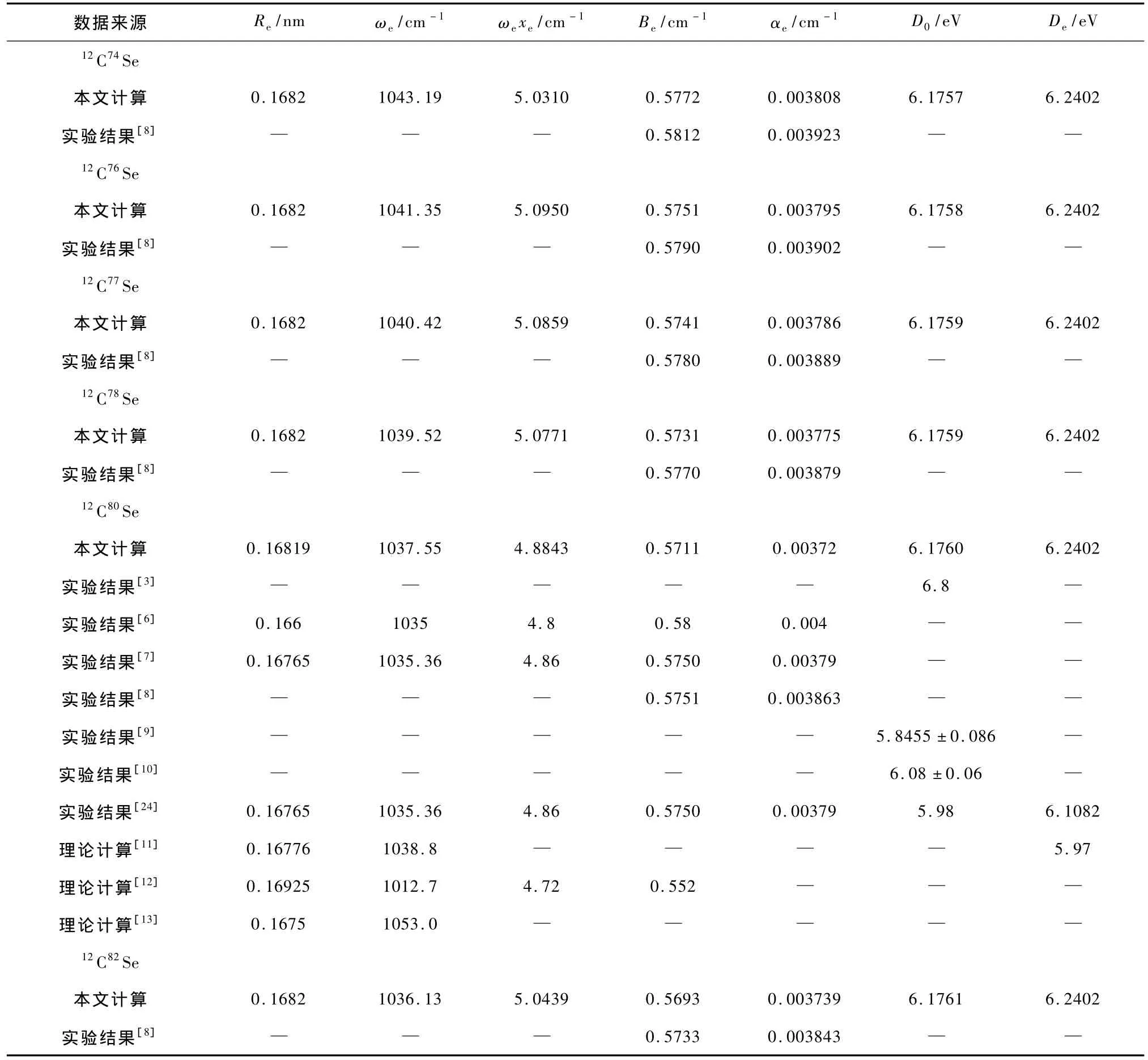
表1 CSe同位素分子基态的光谱常数及其与实验结果和其他理论计算的比较

关于CSe自由基光谱常数的理论研究不多［11—13］．较早的理论工作是由Martin等［11］报道的．Martin等［11］于2001年利用CCSD(T)方法及SDB相对论赝势基结合核极化势计算了重p区多个双原子分子的光谱常数．对于CSe自由基，Martin等［11］得到的基态Re，ωe和De值分别为0.16776 nm，1038.8 cm－1和5.97 eV．这与已有的实验结果均较为一致，如:Re和ωe偏离实验结果［6］分别只有1.06%和0.37%，偏离实验结果［7］也分别只有0.07%和0.33%，是较为准确的;所得离解能也与实验结果［10］较为符合，偏差只有2.26%．但一方面，Martin等［11］只计算了有限个数的光谱常数，同时也未进行同位素识别;另一方面，由于所采用的CCSD(T)方法是单参考态方法，计算结果的可靠性没有多参考态高．

Kalcher［12］于2002年采用CAS-ACPF方法及cc-p VQZ基组计算了CSe(X1Σ+)自由基的Re，ωe，ωexe和Be．与实验结果［6］相比，其Re值超过实验值0.03 nm(1.96%)以上，其ωe，Be及ωexe值分别比实验值低22 cm－1(2.12%)，0.03 cm－1(4.83%)和0.14 cm－1(1.67%);与实验［7］相比，其Re，ωe，ωexe和Be值偏离实验值也分别达到0.0016 nm (0.95%)，22.66 cm－1(2.24%)，0.14 cm－1(2.88%)和0.023 cm－1(4.0%)．显然，本文结果优于Kalcher［12］得到的这些结果．同年，Menconi［13］使用7种交换关联泛函方法及6-311+G(2df)基组计算了CSe自由基基态的Re和ωe．其中最接近实验数据的结果是使用1/4交换关联泛函方法得到的，如表1所列．由表1可见，其Re值与实验结果［6，7］较为一致，ωe值比实验值［6，7］偏高约18 cm－1．由于密度泛函方法的局限性，Menconi［13］未计算该自由基的离解能，同时也未计算该自由基的振动能级等分子常数．

与文献［6］实验相比，本文得到的12C80Se (X1Σ+)同位素分子的Re值仅偏高0.02 nm (1.32%)，ωe和ωexe也只偏高2.55 cm－1(0.25%)和0.009 cm－1(1.76%)，是相当好的．Be偏离实验值［6］虽然有点大，但也只有0.01 cm－1(1.53%)．与实验［7］相比，本文的12C80Se(X1Σ+)同位素分子的Re，ωe，ωexe和Be值与其偏差更小，分别只有0.0005 nm(0.32%)，2.19 cm－1(0.21%)，0.02 cm－1(0.50%)和0.02 cm－1(0.70%)．由此可见，本文计算得到的12C80Se同位素分子的光谱常数具有较高的精度，且优于以往所有的理论结果．

对于其余5个同位素分子12C74Se，12C76Se，12C77Se，12C78Se和12C82Se，文献［8］报道了其Be和α12C74Se12C76Se12C77Se，12C78Se和12C82Se同位素分子的Be值同样具有很高的精度，与其偏差分别只有0.69%，0.67%，0.67%，0.68%和0.70%．尽管计算所得αe值稍微偏小，但偏差也分别在2.93%，2.74%，2.65%，2.68%和2.71%以内．

通过以上比较可以看出，12C80Se同位素分子的光谱常数与实验结果较为一致，它说明本文计算得到的CSe(X1Σ+)自由基的势能曲线是准确可靠的．从拟合过程可以看出，这6种同位素分子的光谱常数都来自于同一势能曲线，且拟合方法都相同．因此，尽管没有更多的光谱实验数据供本文比较，我们依然有理由相信其他5个同位素分子(12C74Se，12C76Se，12C77Se，12C78Se和12C82Se)的光谱数据是可靠的．从这种意义上讲，本文得到的势能曲线能够用来准确预测该自由基各同位素分子的振动能级等分子常数．

3.2.振动能级、振动经典转折点及惯性转动常数

根据计算得到的势能曲线，通过求解核运动的径向Schr dinger方程和进行同位素识别，找到了J =0时CSe(X1Σ+)自由基6个主要同位素分子的全部振动态．如:12C80Se(X1Σ+)和12C78Se(X1Σ+)的振动态总数均为81个，等等．对每一同位素分子的每一振动态，还分别计算了其振动能级、经典转折点、惯性转动常数和离心畸变常数等分子常数．限于篇幅，表2仅列出12C78Se(X1Σ+)和12C80Se (X1Σ+)当J=0时的前20个振动态的振动能级和经典转折点．

由于尚未发现报导CSe(X1Σ+)自由基各同位素分子的振动能级的实验或理论结果，暂时无法将本文计算结果与其进行直接的比较．但前面的讨论已经得出，本文得到的势能曲线是准确的．由于本文计算方法已被证明十分可靠［25—29］，因此作者有理由相信，表2列出的12C78Se(X1Σ+)和12C80Se (X1Σ+)自由基的振动能级和经典转折点数据是准确的．

表3列出了CSe(X1Σ+)自由基6个同位素分子J=0时的前20个振动态的惯性转动常数Bυ．只有文献［6］报导了该自由基前3个振动态的惯性转动常数．为使表3保持整洁，作者将实验［6］中仅有的Bυ值单独列入表4中．比较表3和表4发现，本文得到的B0，B1及B2与实验值［6］分别只相差1.34%，1.48%和1.62%，是很好的．

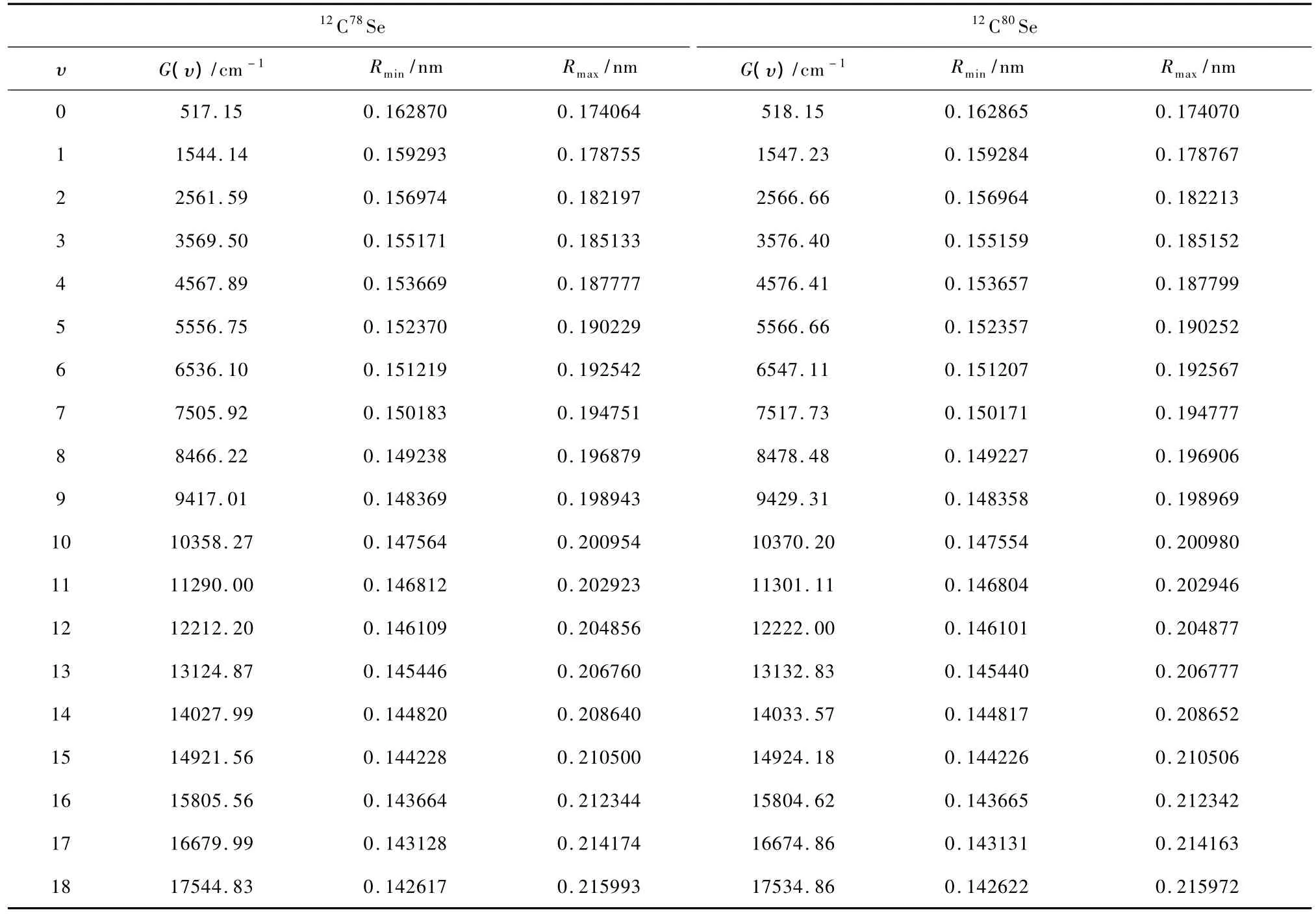
表2 12C78Se(X1Σ+)，12C80Se(X1Σ+)自由基的振动能级和经典转折点(J=0时)

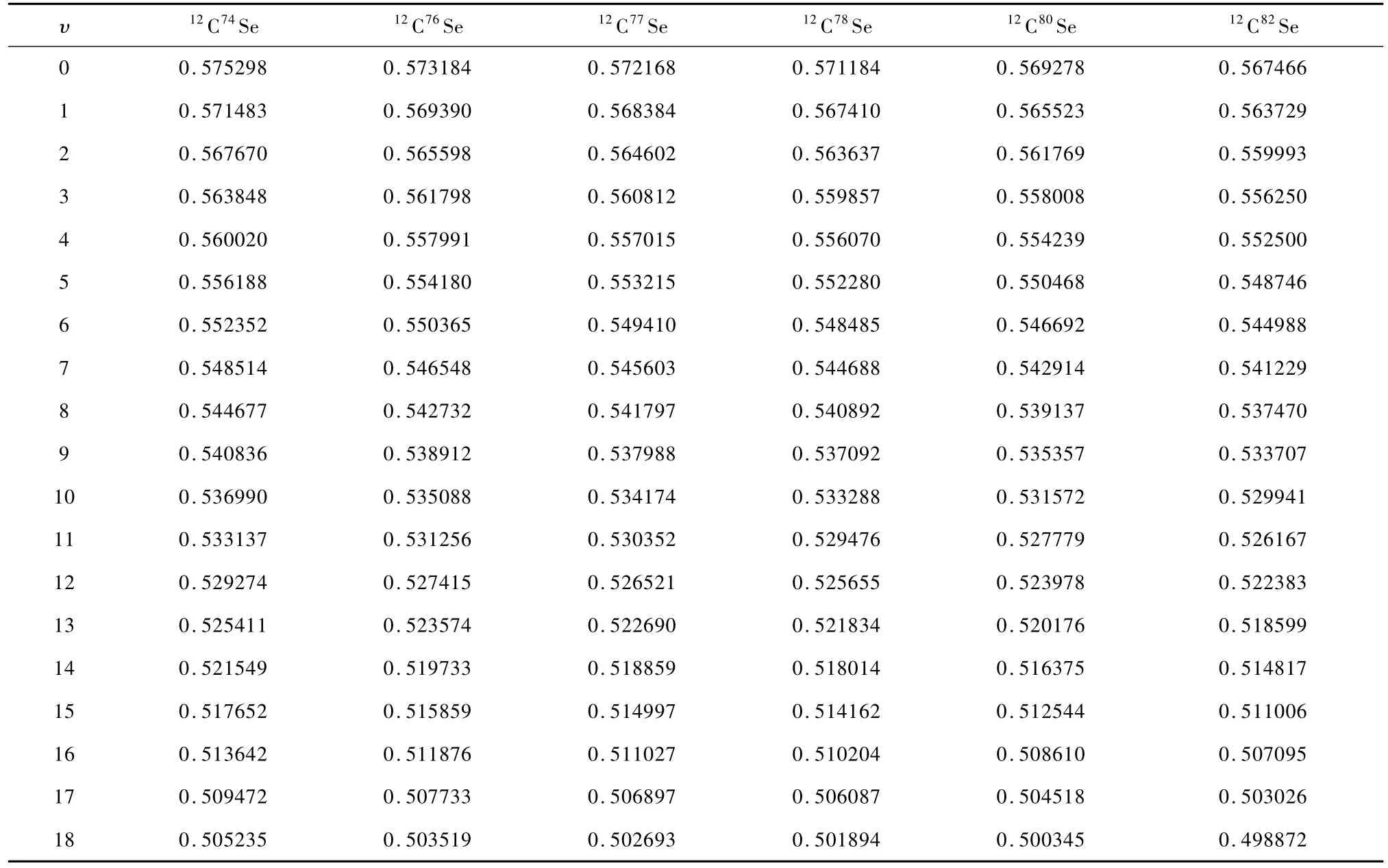
表3 CSe(X1Σ+)自由基的惯性转动常数Bυ(当J=0时)

表4 CSe(X1Σ+)自由基的Bυ实验值(当J=0时)

无论是光谱跃迁还是分子精细结构方面的研究，都需要准确的振转能级数据作为支撑，而实验上获得这些数据往往较为困难．从这种意义上讲，从理论上获得分子的准确振转能级，以便为实验研究提供参考就显得格外重要．为此，作者通过求解振转Schr dinger方程，得到了6种主要同位素分子的振转能级．限于篇幅，这里只列出12C80Se (X1Σ+)自由基的部分计算结果，如表5所示．利用这些数据和跃迁规则，即可计算该态的振转跃迁谱线．

表5 12C80Se(X1Σ+)的振转能级

由于没有找到CSe(X1Σ+)自由基各种同位素分子的振动能级和经典转折点等的实验或理论计算结果，因此无法直接进行比较．但是，根据前文中对CSe(X1Σ+)光谱常数的计算结果与其他理论计算及实验数据的分析比较可以断定，本文计算得到的CSe(X1Σ+)自由基的势能曲线是准确、可靠的，拟合得到的6种同位素的光谱常数及分子常数都是可信的．

4.结论

本文采用高精度的MRCI方法及在C原子使用价态范围内的较大相关一致基aug-cc-pV5Z、Se原子

使用最大赝势基aug-cc-pV5Z-pp的基础上，于0.08—2.5 nm的核间距范围内计算了CSe自由基基态的势能曲线．利用得到的势能曲线并进行同位素质量识别，拟合得到了该自由基6个主要同位素分子12C74Se，12C76Se，12C77Se，12C78Se，12C80Se和12C82Se的光谱常数D0，De，Re，ωe，ωexe，αe和Be，计算结果与实验值较为一致．通过数值求解核运动的径向Schr dinger方程和进行同位素识别，找到了J=0时6个主要同位素分子的全部振动态．针对每一同位素分子的每一振动态，还计算了与其相应的振动能级、经典转折点和惯性转动常数等分子常数．其值与已有的实验结果符合较好．本文的计算结果可为该自由基各同位素分子进一步的实验及理论研究提供参考．

［1］Finn E J，King G W 1975 J．Mol．Spectrosc．56 39

［2］Rosen B，Désirant M 1935 C．R．Acad．Sci．Paris 200 1659

［3］Barrow R F 1939 Proc．Phys．Soc．51 989

［4］Ives D L G，Pittman R W，Wardlaw W 1947 J．Chem．Soc．45 1080

［5］Howell H G 1947 Proc．Phys．Soc．59 107

［6］Laird R K，Barrow R F 1953 Proc．Phys．Soc．A 66 836

［7］McGurk J，Tigelaar H L，Rock S L，Norris C L，Flygare H 1973 J．Chem．Phys．58 1420

［8］Lovas F J，Tiemann E 1974 J．Phys．Chem．Ref．Data 3 609

［9］Radler K，Berkowitz J 1977 J．Chem．Phys．66 2176

［10］Kerr J A，Stocker D W 1999 Handbook of Chemistry and Physics，80 th Ed．(Boca Raton，FL:Chemical Rubber Corp．Press)P240

［11］Martin J M L，Sundermann A 2001 J．Chem．Phys．114 3408

［12］Kalcher J 2002 Phys．Chem．Chem．Phys．4 3311

［13］Menconi G，Tozer D J 2002 Chem．Phys．Lett．360 38

［14］Knowles P J，Werner H J 1988 Chem．Phys．Lett．145 514

［15］Dunning T H 1989 J．Chem．Phys．90 1007

［16］Ermler W C，Ross R B，Christiansen P A 1988 Adv．Quantum Chem．19 139

［17］Krogh J W，Lindh R，Malmqvist P，Roos B O，Veryazov V，Widmark P O 2009 User Manual，Molcas Version 7.4，Lund University

［18］Shi D H，Liu H，Sun J F，Zhu Z L，Liu Y F 2010 Acta Phys．Sin．59 227(in Chinese)［施德恒、刘慧、孙金锋、朱遵略、刘玉芳2010物理学报59 227］

［19］Shi D H，Zhang J P，Sun J F，Liu Y F，Zhu Z L 2009 Acta Phys．Sin．58 2369(in Chinese)［施德恒、张金平、孙金锋、刘玉芳、朱遵略2009物理学报58 2369］

［20］Temelso B，Valeev E F，Sherrill C D 2004 J．Phys．Chem．A 108 3068

［21］Shi D H，Liu H，Sun J F，Zhang J P，Liu Y F，Zhu Z L 2009 J．Mol．Struct．(Theochem)911 8

［22］Werner H J，Knowles P J，Lindh R，Manby F R，Schütz M，Celani P，Korona T，Mitrushenkov A，Rauhut G，Adler T B，Amos R D，Bernhardsson A，Berning A，Cooper D L，Deegan M J O，Dobbyn A J，Eckert F，Goll E，Hampel C，Hetzer G，Hrenar T，Knizia G，K ppl C，Liu Y，Lloyd A W，Mata R A，May A J，McNicholas S J，Meyer W，Mura M E，Nicklass A，Palmieri P，Pflüger K，Pitzer R，Reiher M，Schumann U，Stoll H，Stone A J，Tarroni R，Thorsteinsson T，Wang M，Wolf A MOLPRO，version 2008．1，a package of ab initio programs，http://www．molpro．net

［23］González J L M Q，Thompson D 1997 Comput．Phys．11 514

［24］Huber K P，Herzberg G 1979 Molecular Spectra and Molecular Structure(IV)(New York:Van Nostrand Reinhold Company)

［25］Zhang L，Yang C L，Ren T Q 2008 Mol．Phys．106 615

［26］Shi D H，Liu H，Zhang X N，Sun J F，Zhu Z L，Liu Y F 2010 J．Mol．Struct．(Theochem)956 10

［27］Zhang X N，Shi D H，Sun J F，Zhu Z L 2010 Chin．Phys．B 19 013501

［28］Wang X Q，Yang C L，Su T，Wang M S 2009 Acta Phys．Sin．58 6873(in Chinese)［王新强、杨传路、苏涛、王美山2009物理学报58 6873］

［29］Ma N，Wang M S，Yang C L，Ma X G，Wang D H 2010 Chin．Phys．B 19 023301

PACS:31．15．aj，31．30．Gs，31．50．Bc，31．50．Df

*Project supported by the National Natural Science Foundation of China(Grant Nos．10874064，61077073)，the Program for Science＆Technology Innovation Talents in Universities of Henan Province，China(Grant No．2008 HASTIT008)，and the Natural Science Foundation of Educational Bureau of Henan Province，China(Grant No．2010 B140013)．

Corresponding auther．E-mail:scattering@sina．com．cn

Spectroscopic parameters and molecular constants of CSe(X1Σ+)radical*

Liu Hui1)Shi De-Heng1)Sun Jin-Feng2)Zhu Zun Lüe2)
1)(College of Physics and Electronic Engineering，Xinyang Normal University，Xinyang 464000，China)
2)(College of Physics and Information Engineering，Henan Normal University，Xinxiang 453007，China)
(Received 23 August 2010;revised manuscript received 18 September 2010)

The spectroscopic and molecular properties of CSe(X1Σ+)radical are investigated using the complete active space self-consistent field(CASSCF)method followed by the highly accurate valence internally contracted multireference configuration interaction(MRCI)approach．The potential energy curve(PEC)is calculated over the internuclear separation range from 0．08 to 2．5 nm at the basis sets，aug-cc-pV5Z for C and aug-cc-pV5Z-pp for Se atom．The spectroscopic parameters(D0，De，Re，ωe，ωexe，αeand Be)of six isotope molecules(12C74Se，12C76Se，12C77Se，12C78Se，12C80Se and12C82Se)are evaluated using the PEC of CSe(X1Σ+)radical．The spectroscopic parameters are compared with those reported in the literature，and excellent agreement is found between them．With the PEC of CSe (X1Σ+)radical obtained here，a total of81 vibrational states of12C80Se species are predicted when J=0 by numerically solving the radical Schr dinger equation of nuclear notion．For each vibrational state of every isotope species，the vibrational levels，classical turning points and inertial rotation constants are reported，which are in agreement with the available experimental data．

isotope identification，potential energy curve，spectroscopic parameter，molecular constant

*国家自然科学基金(批准号:10874064，61077073)、河南省高校科技创新人才支持计划(批准号:2008HASTI T008)和河南省教育厅自然科学基金(批准号:2010 B140013)资助的课题．