Full-Heusler合金X2Y Ga(X=Co，Fe，Ni; Y=V，Cr，Mn)的电子结构、磁性及半金属特性的第一性原理研究*

刘新浩林景波刘艳辉金迎九

Full-Heusler合金X2Y Ga(X=Co，Fe，Ni; Y=V，Cr，Mn)的电子结构、磁性及半金属特性的第一性原理研究*

刘新浩 林景波 刘艳辉 金迎九

(延边大学理学院物理系，延吉133002)
(2011年1月6日收到;2011年1月28日收到修改稿)

利用基于密度泛函理论的全势线性缀加平面波方法，结合广义梯度近似，对full-Heusler X2Y Ga(X=Co，Fe，Ni; Y=V，Cr，Mn)合金的电子结构、磁性及半金属特性进行了研究，并讨论了自旋-轨道耦合作用对它们的影响．计算结果表明，自旋-轨道耦合作用对full-Heusler X2Y Ga(X=Co，Fe，Ni;Y=V，Cr，Mn)合金的电子结构，磁性与半金属特性的影响很小．当未考虑自旋-轨道耦合作用时，Co2VGa，Co2CrGa，和Fe2CrGa合金为半金属或准半金属铁磁体，加入自旋-轨道耦合作用后体系的自旋极化率将降低1%左右，它们依然保持很高的自旋极化率．Fe2MnGa，Co2MnGa，Ni2CrGa和Ni2MnGa合金为一般铁磁体，Fe2VGa和Ni2VGa合金为顺磁体．

半金属特性，自旋-轨道耦合，Heusler合金，全势线性缀加平面波方法(FLAPW)

PACS:71．20．－b，75．50．－y，75．50．Cc

1.引言

自旋电子学器件因具有良好的稳定性、体积小、能耗低、数据处理快，以及集成密度高等优点而备受人们的关注．目前自旋电子学器件的研制所遇到的关键问题之一是如何高效率地将自旋电流从磁性材料注入到半导体材料之中．稀磁半导体材料虽然具有很高的自旋极化率但它的居里温度一般很低(低于室温)［1，2］，而传统的铁磁材料虽然具有很高的居里温度却具有很低的自旋极化率只有10%到50%［3］．半金属铁磁体(half-metallic ferromagnet)因具有完全的自旋极化率(100%)，而认为是理想的半导体自旋电子注入源之一［4—6］．在半金属铁磁体中，一种自旋方向的能带呈现金属性，而另一种自旋方向的能带呈现半导体特性，从而导致在费米面附近传导电子的自旋极化率为100%．实验和理论研究表明La0．7Sr0．3MnO3［7］，CrO2［8］，Zinc-blende结构CrAs［9］，half-Heusler NiMnSb［4］，full-Heusler Co2MnSi，Co2FeSi［10，11］等化合物具有半金属特性．在众多的半金属铁磁体中Heusler合金因具有较高的居里温度、较大的磁矩、与闪锌矿结构的半导体相接近的晶体结构而备受关注［12—14］．Heusler合金可分为两种类型，即full-和half-Heusler合金．Full-Heusler合金的化学式为X2YZ，具有L21结构，相当于把四个fcc面心立方结构相互套构而成，其中X和Y代表不同的过渡金属元素(如Fe，Co，Ni，Cu，Mn，Ti和V等)，而Z代表sp元素(如Al，Ga，In，Ge，As和Sn等)．

因为Heusler合金是由多种不同电子结构的元素组合而成，即有局域的d电子轨道又有非局域的sp电子轨道，因此具有复杂的能带结构，进而呈现非常丰富而多样的物理现象，比如半金属特性，磁形状记忆效应等［15，16］．Galanakis等人利用fullpotential screened Korringa-Kohn-Rostoker方法对full-Heusler Co2YAl和Fe2YAl(Y=V，Cr，Mn)等合金进行了理论研究［10］，并预测了许多full-Heusler合金具有半金属特性，而且它们的总自旋磁矩满足Slater-Pauling规则，即Mt=Zt－24(μB/原胞)，其中Mt代表原胞的总自旋磁矩，而Zt代表原胞中价电子的总数目．利用超导量子干涉器件和振动样品磁强计，Umetsu［17］等人研究了Co2CrGa合金，所测得的总磁矩为3.01μB，很好的满足Slater-Pauling规则，表明Co2CrGa合金具有半金属特性．第一性原理计算结果也表明L21结构的Co2CrGa合金具有很高的自旋极化率，约为95%［17］．尽管目前对Heusler合金已经有大量的基于密度泛函理论的文献报道，但大多数文献的能带计算是在忽略自旋-轨道耦合作用的条件下进行的．对Half-Heusler NiMnSb合金的第一性原理研究发现，当考虑自旋-轨道相互作用时，因为费米能级上出现由自旋-轨道耦合所引起的自旋向下态，该合金的自旋极化率由100%变成99%;而含有重元素的Zinc-blende结构MnBi，自旋-轨道耦合作用使该体系的自旋极化率由100%下降到77%［18］．自旋轨道耦合效应在自旋电子学中有关自旋注入、输运和调控等方面起着重要的作用，所以有必要对具有不同晶体结构的化合物中自旋-轨道耦合效应进行广泛的研究．本文利用基于密度泛函理论的全势线性缀加平面波方法结合广义梯度近似研究了full-Heusler X2Y Ga(X=Co，Fe，Ni;Y= V，Cr，Mn)合金的电子结构、磁性及半金属特性，并讨论了自旋-轨道耦合作用对它们的影响．

2.模型与计算方法

Full-和half-Heusler合金的结构如图1所示．在Wyckoff坐标系中，X原子占据4 a(0，0，0)和(1/2，1/2，1/2)的位置;Y原子和Z原子则分别占据4 c (1/4，1/4，1/4)和4d(3/4，3/4，3/4)位置．Half-Heusler合金的化学式为XYZ，具有C1b结构，相当于从full-Heusler合金中把(1/2，1/2，1/2)位置处X原子用空缺代替．

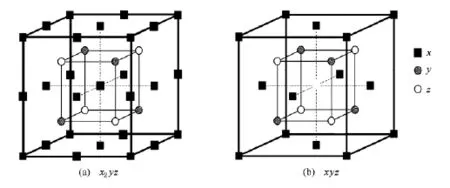
图1 Heusler合金的晶体结构(a)Full-Heusler X2YZ合金;(b)Half-Heusler XYZ合金

因为Fe2Mn Ga，Ni2VGa，Ni2CrGa等合金的晶格常数到目前还没有实验方面的报道，我们通过总能量随晶格常数的变化关系(图1)，得到了三种合金的最优化晶格常数，而对于其他的合金则采用了相应的实验晶格常数．计算得到的Fe2Mn Ga，Ni2VGa，Ni2CrGa等合金的晶格常数分别为5.685，5.797和5.801，它们与以前的理论预测值5.688(Fe2Mn Ga)［19］和5.806(Ni2CrGa)［20］一致．

Kohn-Sham方程的求解是基于密度泛函理论的全势线性缀加平面波(FLAPW)方法［21］(采用FLEUR程序包［22］)结合广义梯度近似(GGA)［23］，以自洽循环来完成．计算中对价电子态考虑了包含和不包含自旋-轨道耦合作用的两种情形［24］．包含自旋-轨道耦合作用时电子本证函数按未包含自旋-轨道耦合作用下Kohn-Sham本证函数的线性叠加展开，相应的展开系数由包含自旋－轨道耦合作用的完全相对论Kohn-Sham方程的对角化来得到．自旋-轨道耦合作用降低体系的对称性．我们把V，Cr，Mn，Fe，Co和Ni原子的3 d4 s态电子取为价电子，而对于Ga原子3d1042p1态电子取为价电子．对Co，Fe，Ni和Mn原子的Muffin－tin半径(RMT)取为1.164，而V，Cr和Ga原子的RMT取为1.217．RMT×Kmax取为～8，平面波展开过程中的能量截断值取为14 Ry．为了描写MT球内电荷密度与势场，基函数球谐函数对应的最大分波数为lmax=8．采用Monhkorst-Pack方法案将布里渊区中的k点进行20 ×20×20的分割．当输入与输出电荷(自旋)密度之差小于1.0×10－5electrons/(a．u．)3时为收敛标准．

3.结果与讨论

3.1.态密度与半金属特性

图2中给出了未含自旋-轨道耦合作用时的X2Y Ga(X=Co，Fe，Ni;Y=V，Cr，Mn)合金的态密度(DOS)．对于自旋向下的态密度乘了－1，Fermi能级(EF)取为0．从图2可以看出，Fe2Y Ga(Y= Cr，Mn)和Co2Y Ga(Y=V，Cr，Mn)等合金的自旋向下的能带在EF附近具有能隙，此时EF位于能隙的和N↓(EF)分别表示EF处自旋向上和自旋向下能带的态密度．与此相反Ni2Y Ga(Y=Cr，Mn)合金具有传统铁磁体的态密度曲线，即EF处自旋向上和向下能带具有不同的态密度值，而X2VGa(X=Fe，Ni)态密度图在两个自旋方向上对称表明这些合金中自旋向上的电子数与自旋向下的电子数相等，即它们的净磁矩为零，为顺磁性合金．以上合金的态密度曲线与以前的相关文献报道［10，17，25，26］相一致．

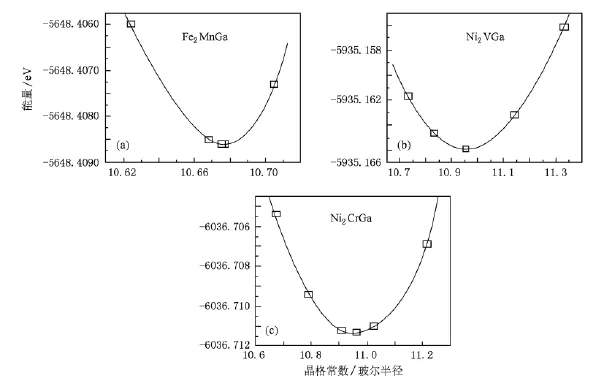
图2 总能量随晶格常数的变化关系(a)Fe2MnGa;(b)Ni2VGa;(c)Ni2CrGa

首先分析Co2VGa合金的态密度．由图2(d)可以看出，在自旋向上的能带中费米能级处上有态密度存在，而在自旋向下的能带中费米能级恰好位于能隙(0.14 eV)的中间，因此Co2VGa合金是具有100%自旋极化率的半金属铁磁体．自旋向下能带中的能隙主要产生于次近邻Co原子3 d态之间的强杂化作用［25］．在高度有序的L21结构中，Co原子处于由次近邻Co原子形成的八面晶体场中，此时Co的3 d轨道分裂为能量较低的t2g和能量较高的eg轨道，虽然Co原子之间是次近邻，但他们之间的轨道杂化作用很大，因而将产生成键态(eg和t2g)与反键态(eu和t1u)轨道;而V原子处于由最近邻Co原子形成的简单立方晶体场中，它的3d轨道分裂为能量较低的eg和能量较高的t2g轨道．按照轨道杂化的对称性匹配原理，最近邻的V原子eg和t2g轨道只跟Co—Co成键态eg和t2g轨道发生杂化而形成成键态eg，t2g轨道和反键态e*g，t2g*轨道，反键态eu和t1u轨道并没有与V的d轨道发生杂化，从而次近邻Co原子之间相互作用所引起的eu和t1u轨道之间的分裂将决定自旋向下能带中能隙的宽度．另外在图2 (d)可以看到，V原子的自旋交换劈裂很小表明V原子具有很小的的自旋磁矩;在自旋向上能带中费米能级以上未填满的态主要是V原子的3d轨道．

当我们用价电子数目跟V原子相比分别多一个和两个的Cr，Mn原子取代Co2VGa合金中的V原子时发现盈余的价电子主要填充自旋向上能带，从而在自旋向上的能带中部分填充的反键态(e*g，)向能量低处移动，导致在Co2CrGa中EF位于Cr原子自旋向上3 d态的尖峰的右侧，而在Co2Mn Ga中EF位于自旋向上反键态轨道的尾部．另一方面，因为Cr，Mn原子的自旋交换劈裂比V原子的大，自旋向下的能带稍微向能量高处移动，使得在Co2Y Ga(Y =Cr，Mn)中EF位于自旋向下能带能隙的左边缘且具有很小的态密度．由于在Co2CrGa的自旋向上能带中EF位于主要来自于Cr3 d态的尖峰的右侧，所以它具有很高的自旋极化率，88%;而Co2MnGa在EF处的自旋向上态密度比较小，它的自旋极化率仅为70%，这与最近的实验结果(60%)比较相近［27］．

因为Fe原子的价电子数目与Co原子相比少一个电子，如果用Fe原子替换Co2Y Ga(Y=V，Cr，Mn)中的Co原子，可以看到虽然Fe2基Heusler合金的自旋向下DOS图与相应的Co2基Heusler合金非常相似，但Fe2基Heusler合金自旋向上DOS与相应的Co2基Heusler合金的相比发生了较大的变化，最明显的是自旋向上DOS中出现了空的Fe3 d轨道(既有t2g态也有eg态的贡献)．由图2(a)—(c)和(d)—(f)的比较，可以看到Fe2基Heusler合金的自旋向下能带中的能隙宽度比Co2基Heusler合金的相比明显缩小，表明Fe2基Heusler合金中Fe原子之间的相互作用与Co2基Heusler合金的Co—Co相互作用相比较弱．此外Fe2基Heusler合金中Cr和Mn的交换劈裂比Co2基Heusler合金的要小，这是由于Cr(或Mn)原子与Fe原子的轨道杂化比Co原子的杂化程度较强导致的．分析表明Fe2VGa为非磁性的半金属(semimetal)，从能带结构图(未给出)发现此时EF附近存在空穴和电子型两个能带，分别位于布里渊区中心Γ点和布里渊区边界X点，这和以前的文献报道一致［28］．

对于Ni2基Heusler合金，由图2(g)—(i)发现Ni2VGa为顺磁性合金，而Ni2Y Ga(Y=Cr，Mn)为一般铁磁性合金，这是由于Ni原子比Co原子多一个价电子，而这些价电子主要填充Ni的自旋向下3 d态，导致EF位于Ni eg态尖峰的右侧．

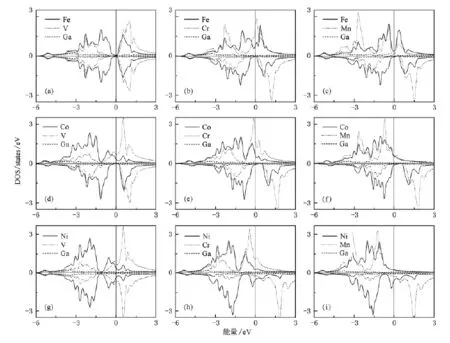
图3 态密度(a)Fe2VGa;(b)Fe2CrGa;(c)Fe2MnGa;(d)Co2VGa;(e)Co2CrGa;(f)Co2MnGa;(g)Ni2VGa;(h)Ni2CrGa; (i)Ni2MnGa

3.2.自旋-轨道耦合作用对半金属特性的影响

为了研究自旋-轨道耦合作用对半金属特性的影响，我们对本论文所研究的合金进行了包含自旋-轨道耦合的第一性原理计算，此时把自旋-轨道耦合作用看成是一种微扰．包含自旋-轨道耦合作用时系统的本证函数是未含自旋-轨道耦合(标量相对论)Kohn-Sham方程的自旋向上和自旋向下本证函数的线性组合．因此系统的按自旋分解的态密度中不仅有来自于自旋向上或自旋向下态密度的贡献，而且有来自于自旋向上和自旋向下态耦合而产生的态密度的贡献［18］．

现对具有半金属特性的Co2VGa进行讨论．在图3中给出了考虑自旋-轨道耦合作用下Co2VGa在EF附近的态密度(实线)，虚线表示未含自旋-轨道耦合作用时的态密度．最显著的特点是在自旋向下能带的能隙中出现了由自旋-轨道耦合引起的微小的态密度，数量级为1.0×10－3，而未考虑自旋-轨道耦合作用时能隙中的态密度为零．由于EF处存在着这种由自旋-轨道耦合作用所引起的微小的态密度，Co2VGa的自旋极化率由100%降低为99%．Mavropoulos等［18］通过screened Korringa-Kohn-Rostoker Green function方法研究了自旋-轨道耦合作用对半金属能隙的影响．研究发现自旋-轨道耦合作用使EF处半金属铁磁体NiMnSb的自旋极化率为99%，而含重元素的半金属铁磁体MnBi的自旋极化率显著降低，仅为77%．对于闪锌矿结构的CaBi，第一性原理研究也发现当不考虑自旋-轨道耦合作用时该体系表现为半金属特性，而考虑了自旋-轨道耦合作用后体系的半金属特性消失［29］．从以上的研究结果，我们看到对于含重元素的体系自旋-轨道耦合作用对自旋极化率的的影响不可忽略，能带计算中必须考虑自旋-轨道耦合作用，而对于Co2VGa和X2CrGa(X=Co，Fe)等合金，因为它们并未含有重元素所以自旋-轨道耦合作用对其能带结构的影响很小，所以体系依然具有很高的自旋极化率．

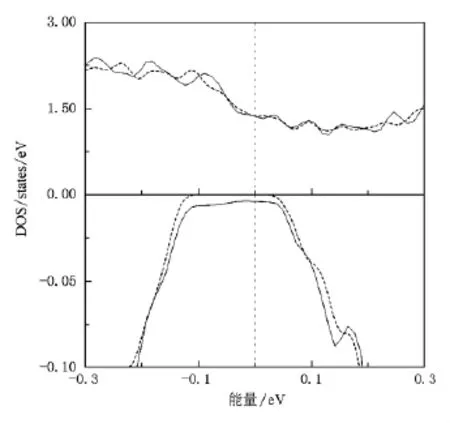
图4 Co2VGa的态密度，实线和虚线分别表示包含和未包含自旋-轨道耦合作用时的态密度

3.3.自旋磁矩与轨道磁矩

在表1，给出了full-Heusler X2Y Ga(X=Co，Fe，Ni;Y=V，Cr，Mn)合金的晶格常数、各原子的自旋磁矩、总磁矩/f．u．和自旋极化率(P)．括号内数据表示包含自旋-轨道耦合作用时相应原子的自旋磁矩/轨道磁矩、总磁矩和自旋极化率．

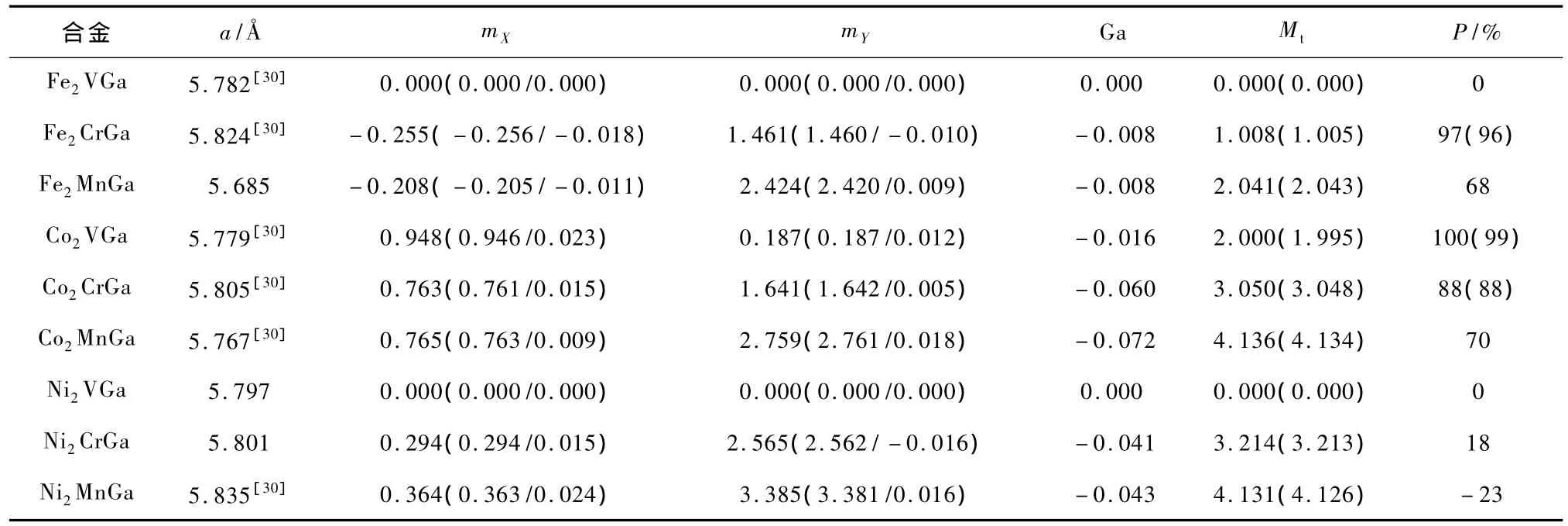
表1 Full-Heusler X2Y Ga(X=Co，Fe，Ni;Y=V，Cr，Mn)合金的晶格常数、各原子的自旋磁矩、总磁矩/f．u．和自旋极化率(P)

从表中可以看出，Co2和Ni2为基的full-Huesler合金中X原子(Co或Ni)的自旋磁矩与Y原子的平行，而Fe2Y Ga(Y=Cr，Mn)中Fe与Y原子的自旋磁矩反平行．未含自旋-轨道耦合作用时Co2VGa合金的总磁矩为整数，即2μB，符合Slater-Pauling规则(总磁矩Mt=Zt－24，其中Zt为价电子总数);而考虑自旋-轨道耦合作用之后总磁矩稍微偏离了整数值，表明半金属特性被破坏，这与态密度的分析相一致．从计算结果可以看到自旋-轨道耦合作用下Cr，Mn，Fe，Co和Ni原子的轨道磁矩与它们的自旋磁矩相比小得很多，其数量级仅为0.01μB，与前人的计算结果基本一致［31，32］．

4.结论

运用全势线性缀加平面波方法结合广义梯度近似，研究了full-Heusler合金X2Y Ga(X=Co，Fe， Ni;Y=V，Cr，Mn)的电子结构，磁性和半金属特性．从总能量随晶格常数的变化关系得到了Fe2MnGa，Ni2VGa和Ni2CrGa合金的最优化晶格常数，它们分别为5.685，5.797和5.801．计算得到的Co2VGa合金的总自旋磁矩为整数，即2μB，满足Slater-Pauling规则;从它的态密度图中也发现EF在自旋向下态的能隙之中，因此该合金为半金属铁磁体，具有100%自旋极化率;Co2CrG和Fe2CrGa的总自旋磁矩分别为3.050和1.008μB，并EF位于此两种合金自旋向下态的能隙的边缘，它们具有很高的自旋极化率(分别为88%和97%);而自旋-轨道耦合作用使体系的自旋极化率降低1%左右．Fe2MnGa，Co2Mn Ga，Ni2CrGa和Ni2Mn Ga合金为一般铁磁体，它们的总自旋磁矩分别为2.041，4.136，3.214和4.131μB;而Fe2VGa和Ni2VGa合金的总自旋磁矩为0，它们为顺磁体．

［1］Ohno Y，Young D K，Beschoten B，Matsukura F，Ohno H，Awschalom D D 1999 Nature 402 790

［2］Fiederling R，Keim M，Reuscher G，Ossau W，Schmidt G，Waag A，Molenkamp L W 1999 Nature 402 787

［3］Soulen Jr R J，Byers J M，Osofsky M S，Nadgorny B，Ambrose T，Cheng S F，Broussard P R，Tanaka C T，Nowak J，Moodera J S，Barry A，Coey J M D 1998 Science 282 85

［4］de Groot R A，Mueller F M，van Engen P G，Buschow K H J 1983 Phys．Rev．Lett．50 2024

［5］Xie W H，Xu Y Q，Liu B G，Pettifor D G 2003 Phys．Rev．Lett．91 037204

［6］Katsnelson M I，Irkhin V Yu，Chioncel L，Lichtenstein A I，de Groot R A 2008 Rev．Mod．Phys．B 80 315

［7］Park J H，Vescovo E，Kim H J，Kwon C，Ramesh R，Venkatesan T 1998 Nature 392 794

［8］Ji Y，Strijkers G J，Yang F Y，Chien C L，Byers J M，Anguelouch A，Xiao G，Gupta A 2001 Phys．Rev．Lett．86 5585

［9］Akinaga H，Manago T，Shirai M 2000 Jpn．J．Appl．Phys．39 L1118

［10］Galanakis I，Dederichs P H and Papanikolaou N 2002 Phys．Rev．B 66 174429

［11］Wurmehl S，Fecher G H，Kandpal H C，Ksenofontov V，Felser C，Lin H J，Morais J 2005 Phys．Rev．B 72 184434

［12］Kandpal H C，Fecher G H，Felser C 2006 Phys．Rev．B 73 094422

［13］Li G N，Jin Y J 2009 Chin．Phys．Lett．26 107101

［14］Li G N，Jin Y J，Lee J I 2010 Chin．Phys．B 19 097102

［15］Ma L，Zhu Z Y，Li M，Yu S D，Cui Q L，Zhou Q，Chen J L，Wu G H 2009 Acta Phys．Sin．58 3479(in Chinese)［马丽、朱永志、李敏、于世丹、崔启良、周强、陈京兰、吴光恒2009物理学报58 3479］

［16］Luo L J，Zhong C G，Quan H R，Tan Z Z，Jiang Q，Jiang X F 2010 Acta Phys．Sin．59 8037(in Chinese)［罗礼进、仲崇贵、全宏瑞、谭志中、蒋青、江学范2010物理学报59 8037］

［17］Umetsu R Y，Kobayashi K，Kainuma R，Fujita A，Fukamichi K，Ishida K，Sakuma A 2004 Appl．Phys．Lett．85 2011

［18］Mavropoulos Ph，Sato K，Zeller R，Dederichs P H，Popescu V，Ebert H 2004 Phys．Rev．B 69 054424

［19］Zayak A T，Entel P，Rabe K M，Adeagbo W A，Acet M 2005 Phys．Rev．B 72 054113

［20］Gillsen M 2009 Ph．D．Thesis(Achen:Rwth Aachen University)(in German)

［21］Wimmer E，Krakauer H，Weinert M and Freeman A J 1981 Phys．Rev．B 24 864 Weinert M，Wimmer E，Freeman A J 1983 Phys．Rev．B 26 4571

［22］http://www．flapw．de

［23］Perdew J P，Burke K，Ernzerhof M 1996 Phys．Rev．Lett．77 3865;1997 ibid．78 1396(E)

［24］Li C，Freeman A J，Jansen H J F，Fu C L 1990 Phys．Rev．B 42 5433

［25］Galanakis I，Dederichs P H，Papanikolaou N 2002 Phys．Rev．B 66 134428Galanakis I，Mavropoulos P，Dederichs P H 2006 J．Phys．D: Appl．Phys．39 765

［26］Kandpal H C，Fecher G H，Felser C 2007 J．Phys．D:Appl．Phys．40 1507

［27］Varaprasad B S D Ch S，Rajanikanth A，Takahashi Y K，Hono K 2010 Appl．Phys．Express 3 023002

［28］Bansil A，Kaprzyk S，Mijnarends P E，Toboa J 1999 Phys．Rev． B 60 13396

［29］Li Y，Yu J J 2008 Phys．Rev．B 78 165203

［30］Buschow K H J，van Engen P G，Jongebreur R 1983 J．Magn．Magn．Mater．38 1

［31］Sargolzaei M，Richter M，Koepernik K，Opahle I，Eschrig H，Chaplygin I 2006 Phys．Rev．B 74 224410

［32］Galanakis I 2005 Phys．Rev．B 71 012413

PACS:71．20．－b，75．50．－y，75．50．Cc

First-principles study on the electronic structures，magnetism，and half-metallicity of full-Heusler X2Y Ga (X=Co，Fe，Ni;Y=V，Cr，Mn)alloys*

Liu Xin-Hao Lin Jing-Bo Liu Yan-Hui Jin Ying-Jiu
(Department of physics，College of Science，Yanbian University，Yanji 133002，China)
(Received 6 January 2011;revised manuscript received 28 January 2011)

Using the full-potential linearized augmented plane wave method within the generalized gradient approximation，we investigatete the electronic structures，magnetisms and half-metallicities of the full-Heusler X2Y Ga(X=Co，Fe，Ni;Y= V，Cr，Mn)alloys．It is found that the spin-orbit coupling has little effect on the electronic structures，magnetisms and half-metallicities of the full-Heusler X2Y Ga(X=Co，Fe，Ni;Y=V，Cr，Mn)alloys．Without spin-orbit coupling the Co2VGa，Co2CrGa，and Fe2CrGa alloys are half-metallic or nearly half-metallic ferromagnets．With including the spin-orbit coupling，the spin-polarizations are lowered by about 1%，thus they still remain high spin-polarizations．The Fe2MnGa，Co2MnGa，Ni2CrGa，and Ni2MnGa alloys are conventional ferromagnets，whereas the Fe2VGa and Ni2VGa alloys are paramagnets．

half-metallicity，spin-orbit coupling，Heusler alloys，full-potential linearized augmented plane wave method (FLAPW)

*国家自然科学基金(批准号:10664005，10864008，11064015)和教育部留学回国人员科研启动基金(批准号:［2007］1108)资助的课题．

．E-mail:jinyingjiu@ybu．edu．cn

*Project supported by the Natural Science Foundation of China(Grant Nos．10664005，10864008，11064015)and the SRF for ROCS，SEM (Grant No．［2007］1108)．

Corresponding author．E-mail:jinyingjiu@ybu．edu．cn