电力系统电磁转矩系数的性质及其计算方法①
郝正航, 王映康, 李健波, 樊 容, 魏 猛
(1.天津大学电气与自动化学院, 天津 300072; 2.贵州大学电气工程学院, 贵阳 550003; 3.重庆渝电信息通信有限公司, 重庆 400014; 4.重庆铜梁县供电有限责任公司, 重庆 402500)
电力系统电磁转矩系数的性质及其计算方法①
郝正航1,2, 王映康3, 李健波4, 樊 容3, 魏 猛4
(1.天津大学电气与自动化学院, 天津 300072; 2.贵州大学电气工程学院, 贵阳 550003; 3.重庆渝电信息通信有限公司, 重庆 400014; 4.重庆铜梁县供电有限责任公司, 重庆 402500)
为了揭示电磁转矩系数的实质,证明了用电磁转矩系数表达电磁转矩只是某种近似,还证明了将单机系统的电磁转矩定义推广于多机系统,其前提条件是所研究的机组相对于惯性中心COI(center of inertia)只有1个运动模式;基于状态空间模型,提出了单机、2机和2机群的电磁转矩系数的定义,给出了理论计算方法。在多机情形下,针对某一模式将系统视为2个机群,通过广域测量系统得到局部系统COI的转速和功角、各发电机电磁功率,从而不需等值运算而转化为等值2机,并测辨其电磁转矩系数。算例分析表明,所提出的电磁转矩系数的理论计算和辨识方法是有效的,二者能够相互印证。
电力系统; 电磁转矩; 在线辨识; 广域测量系统; 小扰动稳定
电力系统机电振荡分析有两种基本方法[3]:其一是根据线性化状态空间模型进行特征分析,即计算系统矩阵的特征值和特征向量,从而得到振荡频率、阻尼和振型;其二是基于物理意义的电磁转矩分析方法,将作用在转子上的电磁转矩分解为阻尼转矩和同步转矩,根据两种转矩的数值大小判断同步发电机的小扰动稳定性。一般认为,阻尼转矩过小或为负值将导致低频振荡。
电磁转矩的概念不但在早期文献[4~6]中有较多论述,而且至今仍是阻尼分析与控制的理论基础[7~13]。文献[4]在单机无穷大系统中,给出了电磁转矩的定义并使用最小二乘法计算。文献[5]基于派克方程推导了电磁转矩系数的计算公式,但没有考虑励磁调节器。文献[6]分别计算励磁绕组、阻尼绕组和PSS提供的电磁转矩,再用叠加原理得到总的电磁转矩。文献[7,8]提出了基于神经网络和卡尔曼滤波的辨识方法,该算法的抗噪性能好。文献[9,10]将电磁转矩的概念推广到多机系统并提出计算方法和用于阻尼控制。文献[11]通过在线辨识阻尼转矩,预测振荡稳定极限。文献[12]基于Heffron-Phillips模型讨论了电磁转矩系数,并导出与机电特征值的关系。
对电磁转矩分析理论的研究,目前有3个关键问题尚未得到很好的解决:
①电磁转矩系数的定义和计算方法是基于单机无穷大系统提出的,可否直接推广于多机电力系统仍然存在疑问;
②电磁转矩系数的定义是从辨识角度提出的,定义不够严谨,需要更深入的科学论证和完善;
③电磁转矩法与特征分析法的联系没有建立;电磁转矩系数的理论计算以及在多机电力系统中的应用尚无深入研究。
本文将针对上述问题进行深入讨论并提出解决途径。
1 电力系统电磁转矩的定义
1.1 单机无穷大系统的电磁转矩定义
电力系统电磁转矩(ΔTe)的最早定义是基于单机无穷大系统的,后来Demello和Concordia用这一概念分析低频振荡[4]。电磁转矩的定义式为
ΔTe(t)=KdΔω(t)+KsΔδ(t)
(1)
式中:Δω和Δδ分别是发电机的转速和功角增量;Kd和Ks分别称为阻尼转矩系数和同步转矩系数,它们的数值大小和符号可以决定系统的小扰动稳定性。为了后文表达方便,本文补充电磁转矩系数的规格化定义,即KdN=Kd/H,KsN=Ks/H。H是发电机惯性时间常数。
1.2 多机电力系统的电磁转矩定义
电磁转矩在单机无穷大系统中提出定义后,提出者并没有进一步推广至多机系统,而后来的不少研究者试图在多机电力系统中建立其定义。其形式[9,10]为
ΔTe,i(t)=Kd,iΔωi(t)+Ks,iΔδi(t)
(2)
式中:Δωi(t)和Δδi(t)是第i台机相对于惯性中心COI(center of inertia)的转速和功角。可见,式(2)只是式(1)的简单推广。
俄国学者还提出过另一种形式[12],即
(3)
式(3)对电磁转矩的表达与式(2)不同,它将电磁转矩分解为n-1个分量,认为第i台机的电磁转矩和其他n-1台发电机相对转速、相对功角有关。
2 电磁转矩系数的数学本质与物理本质
2.1 电磁转矩系数的存在性分析
综观以往文献,电磁转矩表达形式多样化。若不对其深入分析而应用,则可能导致错误。为了从数学上认识它,给出命题1。
命题1在实数范围内,严格满足式(1)~式(3)的电磁转矩系数Kd和Ks、Kd,i和Ks,i,Kd,ij和Ks,ij都不存在。
证明:使用反证法。首先考察单机无穷大系统。假设存在Kd和Ks使式(1)成立。根据电力系统暂态分析理论,同步电机电磁转矩是横、纵轴次暂态电势和功角的多元函数,表示为
(4)
根据式(4),小扰动下的偏差方程为
(5)
正常运行条件下,C1和C2不全为零。将式(5)代入式(1)可得

(6)
由于不存在满足式(1)~式(3)的电磁转矩系数(阵),所以用电磁转矩系数表达电磁转矩只是某种近似。以上三式本质上都是矛盾方程组,求解电磁转矩系数就是求解矛盾方程的近似解。
2.2 电磁转矩系数与系统动态等值的关系
电磁转矩系数除了原始的物理意义外,本文给出另一物理解释。首先讨论单机情形,假设原动机机械转矩Tm恒定,转子运动方程可表达为

(7)
式(1)代入式(7),并考虑规格化定义,得

(8)
由此可见,当电磁转矩用式(1)表达时,转子运动方程中不再包含Δδ及Δω之外的其他状态变量,相当于将详细模型X=AX等值为二阶模型。所以,求解Kd和Ks,本质上就是进行动态等值。
等值后的系统不再包含转子各绕组磁链模式、励磁机模式及调节器模式,仅剩机械模式。
依据系统等值观点,式(8)表达的降阶系统特征值应该等于原系统的机电特征值(λ=σ±jω)。因此,问题转化为:当Kd和Ks取何值时,降阶系统(式(8))特征值等于期望(原系统)特征值。
可见,这是给定特征值求微分方程系数的问题,属代数特征值反问题的范畴[13]。对于单机(或二机)系统,该反问题的解存在且唯一。对于式(8),反问题的解为
(9)
对于多机情形(式(2)),同样表达的是系统等值关系。仿照前面不难分析,式(2)将多机系统等值为

(10)
式(10)表明,第i台机相对于COI的运动是独立的,以二阶微分方程表达,只能体现一个振荡模式的动态行为。或者说,第i台机在COI坐标下的转子摇摆曲线只包含一个频率。据此可以提出如下命题。
命题2在多机系统中,将电磁转矩表示为式(2)的前提条件是,所研究的机组相对于COI只有一个主导模式。该条件是苛刻的。
最后考察式(3),它表达的也是一种动态等值方案。等值系统为
从系统等值观点,式(11)的n-1对特征值应和原系统n-1对特征值相等,也属于一类矩阵特征值的反问题。然而遗憾的是,该类特征值反问题的解是不确定的,即可能无解,也可能多解[13]。即,无法保证电磁转矩系数阵的存在性和唯一性。故式(3)定义的科学性还需商榷。
(11)
综上所述,电磁转矩系数的数学本质是线性矛盾方程组的近似解,或者是特征值反问题的解;物理本质是仅保留机电模式条件下,对原系统的降阶等值表达。
3 电磁转矩系数的理论计算
3.1 基于状态空间模型的电磁转矩系数的定义
应当说明,式(1)和式(2)的电磁转矩定义是从辨识角度提出的,求解Kd、Ks(Kd,i、Ks,i)只能以“曲线拟合”的手段得到最小二乘解[4,8](即辨识值)。为了评价辨识值的有效性,也为了沟通电磁转矩法与状态空间法之间的联系。下面提出一种定义及计算方法。
基于状态空间模型,从物理意义出发,给出2机(2区)系统电磁转矩系数的定义。
定义1在二机系统中,规格化的电磁转矩系数定义如下:
KdN=Re[G(s)]s=jωd,KsN=-Im[G(s)]s=jωd,
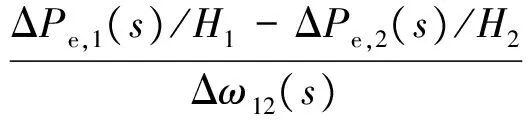

定义2在A、B二区域多机系统中,规格化的电磁转矩系数定义如下:
KdN=Re[G(s)]s=jωd,KsN=-Im[G(s)]s=jωd,其中


对定义2的说明:定义2是对定义1的推广,用子系统(局部)惯性中心的转速,代替定义1中单台电机转速;用子系统各电机功率和,代替单台电机功率。所以,定义2的物理意义仍然是明确的。
3.2 电磁转矩定义在多机系统的推广问题

4 电磁转矩系数的在线辨识
由第3节的定义可见,电磁转矩系数的理论计算运算量很大,超过了特征分析法的计算量,但作为理论研究的基本环节是必要的。电磁转矩系数的在线辨识往往更具实用性。单机情形已有较多研究,以下着重讨论2机及多机系统的情况。
4.1 二机系统电磁转矩系数在线辨识
仿照单机系统Kd、Ks的辨识方法[4],提出2机系统的辨识方案:设2机系统的ΔPe,1,ΔPe,2、Δω12和Δδ12均通过广域测量系统(WAMS)获得N个采集数据。假设
ΔPe,1(i)/H1-ΔPe,21(i)/H2=
KsNΔδ12(i)+KdNΔω12(i)
i=1,2,…,N
(12)
令:ΔP=ΔPe,1/H1-ΔPe,2/H2
B=[ΔP(1),ΔP(2),…,ΔP(N)]T;
A1=[Δδ12(1),Δδ12(2),…,Δδ12(N)]T;
A2=[Δω12(1),Δω12(2),…,Δω12(N)]T;
A=[A1,A2];K=[KsN,KdN]T
则式(12)的矩阵表达式为
AK=B
(13)
由命题1知,式(13)是关于K的矛盾方程组。根据数值代数理论,该矛盾方程的法方程为ATAK=ATB,法方程的解K=(ATA)-1ATB是式(13)的最小二乘解,由此得出KdN、KsN的估计值。
4.2 多机系统电磁转矩系数在线辨识

5 算例分析
5.1 2种理论计算结果比较示例
为了检验本文提出的基于状态空间模型的电磁转矩定义与文献[5]定义的等价性,以单机无穷大系统为例(系统参数见文献[17]),采用2种定义分别计算Kd和Ks。计算结果如表1所示。
从表1看出,在各种负荷水平下,2种定义的相对误差均小于3×10-3。可见,2种定义是等价的,微小误差是由计算工具有限精度所致。定义1是建立在状态空间模型上,适用于任何复杂程度的模型。而文献[5]定义不能考虑调节器作用。

表1 单机无穷大系统电磁转矩系数2种理论计算结果的比较(p.u.)
5.2 多机系统功角轨迹功率谱分析
4机2区域电力系统如图1所示,系统参数见文献[6]。为了说明多机系统中电磁转矩法的局限性,首先考察功角轨迹功率谱。图2是受扰后发电机功角摇摆轨迹的功率谱。

图1 2区域4机示例系统
功率谱波峰分布直观地显示了时域信号所包含的频率成分。图2(a)是发电机G2在COI坐标下的功角摇摆曲线的功率谱。可以看出,它包含3.422 rad/s和6.076 rad/s两个频率成分。如4节所述,这正是不能用式(2)表达其电磁转矩的原因。图2(b)是区域1和区域2局部COI的相对摇摆轨迹的功率谱,该谱只有一个显著模式,频率为3.422 rad/s,即区间摇摆模式,故等值为2机。
5.3 2区域系统电磁转矩计算与辨识
为检验定义2的合理性,按此定义计算图1示例系统的电磁转矩系数。先采用格式化的方法形成系统矩阵A,然后依定义2求出传递函数并得到不同负荷水平下的KdN和KsN,即理论计算结果。同时验证第4.2节的在线辨识方案,基于电力系统分析综合程序(PSASP),建立仿真系统并设计扰动试验,采集受扰系统轨迹数据,按第4.2节方法和步骤,得KdN和KsN,即辨别值。 基于定义2和第4.2节辨识方法的两种计算结果均列入表2。

图2 发电机功角摇摆轨迹的功率谱分析

区域1有功出力P机电特征值定义2KdN测辨值KdN定义2KsN测辨值KsN12.2-0.1336±j3.42200.28310.270811.93011.46212.4-0.1275±j3.41100.27220.259411.86411.39912.6-0.1209±j3.40000.26050.248111.79511.32212.8-0.1140±j3.38910.24810.234711.72311.24413.0-0.1066±j3.37700.23480.222111.64711.160
由表2可见,定义2的理论值和辨识值是接近的,同时还看到,电磁转矩系数和特征值的关系与式(9)相符,达到三者相互统一和印证。
6 结语
本文证明了电力系统的电磁转矩表达式不能恒等,只是近似相等。这种近似关系和动态等值存在内在联系,求解电磁转矩系数过程就是动态等值的过程,从而揭示了电磁转矩系数的数学本质和物理本质。在单机或2机系统中,等值系统保留了原系统完整的机电动态,但在多机系统中,等值系统只能保留一个主要模式,由此在多机系统中推广电磁转矩的定义需要苛刻的假设条件。为了使电磁转矩分析法在理论上更加完整,并为在线辨识提供参考标准,本文还基于状态空间模型,提出了电磁转矩系数理论计算公式。在多机系统中,电磁转矩系数的在线辨识应在分群基础上进行,针对某一模式划分为2机群,按等值2机进行电磁转矩系数辨识是可行的。
[1] 徐政. 交直流电力系统动态特性行为分析[M]. 北京: 机械工业出版社, 2005.
[2] 周双喜, 苏小林(Zhou Shuangxi, Su Xiaolin). 电力系统小干扰稳定性研究的新进展(Advance of study on small disturbance stability of power systems)[J].电力系统及其自动化学报(Proceedings of the CSU-EPSA), 2007, 19(2) : 1- 8, 34.
[3] 姜齐荣, 陈湘, 王天,等(Jiang Qirong, Chen Xiang, Wang Tian,etal). 多机系统复转矩系数分析及PSS参数计算(Analysis of complex torque coefficient in multi-machines system and PSS parameters assignment)[J].电力系统及其自动化学报(Proceedings of the CSU-EPSA), 2010, 22(1): 20-25.
[4] DeMello F P,Concordia C. Concept of synchronous machine stability as affected by excitation control[J].IEEE Trans on Power Systems, 1969, 88(4): 316-329.
[5] 高景德, 王祥珩, 李发海. 交流电机及其系统的分析[M].北京: 清华大学出版社,1992.
[6] Kundur P. Power System Stability and Control[M].New York: McGraw-Hill, 1994.
[7] Abu-Al-Feilat E, Bettayeb M, Al-Duwaish H,etal.Neural network-based approach for on-line dynamic stability assessment using synchronizing and damping torque coefficients[J].Electric Power Systems Research, 1996, 39(2): 103-110.
[8] Abu-Al-Feilat E A, Younan N, Grzybowski S. Estimating the synchronizing and damping torque coefficients using Kalman filtering[J].Electric Power Systems Research, 1999, 52(2): 145-149.
[9] Shaltout A A, Abu Al-Feilat K A. Damping and synchronizing torque computation in multi-machine power systems[J].IEEE Trans on Power Systems, 1992, 7(1): 280-286.
[10]Swift F J, Wang H F. The connection between modal analysis and electric torque analysis in studying the oscillation stability of multi-machine power systems[J].International Journal of Electrical Power and Energy System, 1997, 19(5): 321-330.
[11]Ghasemi Hassan, Canizares Claudio. On-line damping torque estimating and oscillatory stability margin prediction[J].IEEE Trans on Power Systems, 2007, 22(2): 667-674.
[12]王青,闵勇,张毅威(Wang Qing, Min Yong, Zhang Yiwei).多机电力系统电磁转矩分析方法(Electric torque analysis in multi-machine power systems)[J].清华大学学报:自然科学版(Journal of Tsinghua University:Sci & Tech), 2008,48(1):9-12.
[13]周树荃,戴华. 代数特征值反问题[M]. 郑州: 河南科学技术出版社, 1990.
[14]余贻鑫. 线性系统[M]. 北京: 科学出版社, 2009.
[15]李鹏,余贻鑫,孙强,等(Li Peng, Yu Yixin,Sun Qiang,etal).基于Prony分析的多机系统电磁转矩系数计算(Computation of electric torque in multi-machine power systems based on Prony analysis)[J].电网技术(Power System Technology),2006,30(10):39-44.
[16]赵书强, 常鲜戎, 潘云江,等(Zhao Shuqiang, Chang Xianrong, Pan Yunjiang,etal). 基于部分惯量中心等值的多机系统特征根计算(A partial center of inertia transformation based method for calculating eigenvalues of multi-machine power system)[J].电力系统自动化(Automation of Electric Power Systems), 1998,22(9):43-45,76.
[17]赵书强,常鲜戎,贺仁睦,等(Zhao Shuqiang, Chang Xianrong, He Renmu,etal). PSS控制过程中的借阻尼现象与负阻尼效应(Borrow damping phenomena and negative damping effect of PSS control)[J].中国电机工程学报(Proceedings of the CSEE),2004,24(5):7-11.
CharacterofElectricTorqueCoefficientsinPowerSystemandItsComputation
HAO Zheng-hang1,2, WANG Ying-kang3, LI Jian-bo4, FAN Rong3, WEI Meng4
(1. School of Electrical Engineering and Automation, Tianjin University, Tianjin 300072, China; 2.School of Electrical Engineering, Guizhou University, Guiyang 550003, China; 3.Chongqing Yudian Information & Communication Company Limited, Chongqing 400014, China; 4.Chongqing Tongliang Power Supply Company Limited, Chongqing 402500, China)
In order to investigate the essence of electrical torque coefficients, it is proved that the equation between active power and electric torque based on two coefficients is not satisfied completely and electric torque method lead to a simplified path of accurate power system model essentially. If the electric torque definition of single machine is applied to multi-machine system, the given machine must be dominated by only one oscillation mode on the center of inertia(COI). This paper also presents electric toque definition and calculating method which can be used for single machine system, two-machine system, and two-area system. In large power system, a two-area system is defined in term of certain mode and its electric torque coefficient can be computed with measured signals (e.g.speed, angle based on partial COI and active power) from wide area measurement system(WAMS). A four-machine system case showed that the methodology proposed can be utilized to identify the coefficient of electric torques.
power system; electric torque; on-line identification; wide area measurement system(WAMS); small-signal stabilit
2010-03-05
2010-11-16
TM743
A
1003-8930(2011)01-0086-06
郝正航(1972-),男,博士研究生,副教授,研究方向为电力系统稳定和风力发电。Email:haozhenghang@163.com 王映康(1965-),男,生产技术部主任,研究方向为电力系统自动化。Email:wyk@cq.sgcc.com.cn 李健波(1970-),男,副总经理,研究方向为电力系统自动化。Email:li.jb@cq.sgcc.com.cn

