灰色马尔柯夫模型在建筑工程坍塌事故预测中的应用

刘红艳 苏曼曼

（1.青岛东方监理有限公司，青岛 266071；2.中国海洋大学，青岛266100）

灰色马尔柯夫模型在建筑工程坍塌事故预测中的应用

刘红艳1苏曼曼2

（1.青岛东方监理有限公司，青岛 266071；2.中国海洋大学，青岛266100）

以建筑施工过程中频发的坍塌事故为研究对象，将灰色GM（1,1）模型与马尔柯夫预测技术相结合，构建坍塌事故的灰色马尔柯夫预测模型，并以我国三级以上建筑工程坍塌事故统计数据为基础，对我国坍塌事故进行趋势分析和状态预测。

坍塌事故；GM(1,1)模型；灰色马尔柯夫预测；建筑工程

建筑施工中，坍塌事故的危害程度最为严重。坍塌往往出现在不同的施工阶段和施工部位，一旦出现容易造成大面积的伤害，发生群死群伤事件，而且会对工程的施工安全、质量、进度造成很大的影响，给人民生命财产造成巨大损失。同时，坍塌事故也是建筑安全事故中最为严重的频发事故。

由于建筑工程坍塌事故具有不确定性、随机性和突变性，因此表征坍塌事故的的参数是随机变化的灰数。然而，灰色GM（1,1）模型作为普遍使用的事故预测方法，适用于原始数据较平缓的序列，对于随机波动性较大数据列的拟合则较差，预测精度较低。灰色马尔柯夫预测模型是灰色GM（1，1）模型与马尔柯夫预测技术相结合的方法，GM(1,1)用来揭示预测数列的发展变化总趋势，而马尔柯夫概率矩阵预测则用来确定状态的转移概率。这种预测模型将两种方法的优势互补，充分利用历史数据给予的信息，大大提高了随机波动较大数据列的预测精度。

本文采用灰色马尔柯夫预测模型，以建筑工程坍塌事故数作为灰色量，预测和分析坍塌事故的未来状态和发展趋势，旨在帮助建设行政主管部门深入分析我国建筑安全生产形势，对薄弱环节采取有针对性的事故防范措施，提高安全生产工作的主动性和预见性。

1 建筑工程坍塌事故灰色马尔柯夫模型的构建

建筑工程坍塌事故的发生受诸多因素的影响，具有很大的随机性和不确定性，灰色特征明显，故可将坍塌事故的产生过程视为一个灰色系统，将事故数作为灰量，收集一定时间的事故数据建立预测模型。

1.1 建立灰色GM（1,1）模型

GM(1,1)模型是灰色预测系统中最普遍的一种预测方法。其建模方法和步骤为：

将建筑工程坍塌事故数（原始数据）X(0)={x(0)(1)，x(0)(2)，x(0)(3)，…，x(0)(n)}作一次累加生成新序列：

构造数据矩阵B，YN，用最小二乘法求解参数向量 a，b:

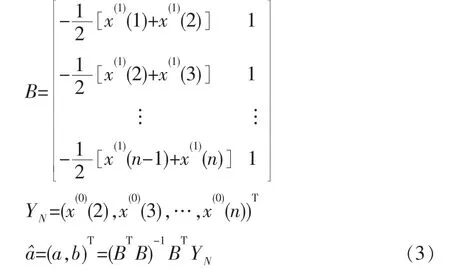
求得时间响应函数式，还原生成预测值时间响应函数为：

1.2 状态划分

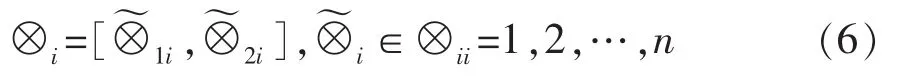
1.3 计算状态转移概率

式中：Mij(m)为由状态⊗i经过m步转移到状态⊗j的原始数据样本数；Mi为处于状态⊗i的原始样本数，由于数据序列最后的状态转向不确定，因此计算Mi时应去掉数据序列中最后m个年份。

由Pij(m)构成状态转移概率矩阵：

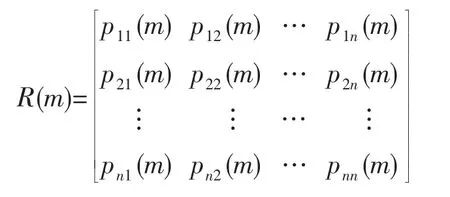
在实际运用过程中，通常只需考察一步转移概率矩阵R(1)就可以，如果R(1)中第k行出现两个以上相近或相同的概率时，系统的未来状态转向是难以确定的，此时就需要考察第二步或者多步转移概率矩阵R(m)(m≥2)。

1.4 确定预测转向状态、预测值的变动区间和预测值

选取离预测年份最近的m个年份，按距离预测年份的近远，将转移步数分别定为1，2，3，…，m。在转移步数所对应的转移矩阵中，取起始状态所对应的行向量，即为各状态出现的概率，对各状态的概率求和并归一化，其中概率最大的状态即为系统随机变量的预测转向状态。

通过考察一步或多步转移概率矩阵，确定了系统未来的转移状态后，也就确定了灰元即确定了预测值的变动灰区间为从而计算得出最可能的预测值

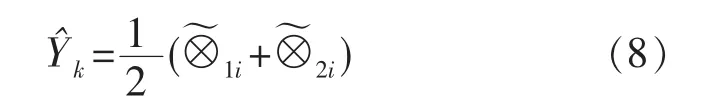
2 实例研究

本文将我国1998～2009年三级以上建筑工程坍塌事故数统计形成一个原始数据序列，进行未来事故的预测（表1）。

表1 1998～2009年三级以上建筑工程坍塌事故数

2.1 构造灰色GM(1,1)模型

由表1可确定原始数据序列为X(0)={12，17，14，15，30，28，20，21，24，19，20，15}，累加生成新序列X(1)={12，29，43，58，88，116，136，157，181，200，220，235}，同时得到 B，YN，求解得到参数向量

则坍塌事故灰色GM（1，1）模型为：

2.2 状态划分

根据定义的状态划分标准，可确定每一年实际数据所处的状态（表3）。

2.3 计算状态转移概率

由表3状态划分结果按式（7），计算1,2,3步转

表2 划分状态标准

表3 建筑工程坍塌事故状态划分

移概率矩阵 R(1)，R(2)，R(3)，结果如下：

2.4 确定预测转向状态、预测值的变动区间和预测值

编制2010～2011年坍塌事故数的灰色马尔柯夫预测表确定预测值的变动区间，并计算预测值，结果见表4。

表4 2010年灰色马尔柯夫状态预测表

由此可知，2010年的预测状态为⊗2，按式（8）得2010年的预测值，具体数据见表5。

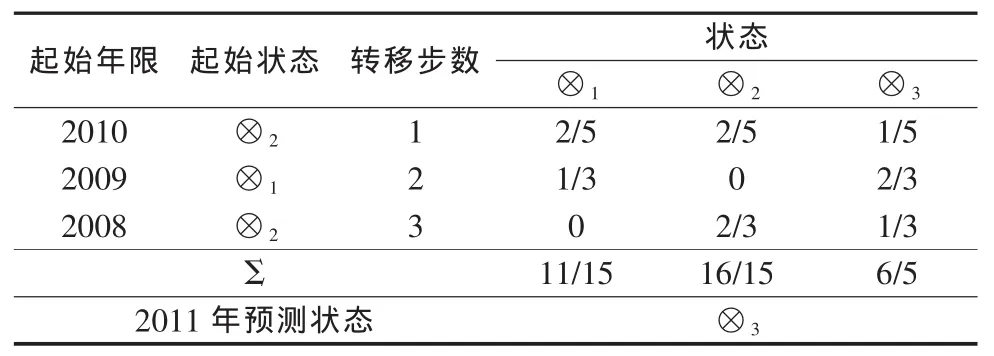
表5 2011年灰色马尔柯夫状态预测表

由此可知，2011年的预测状态为⊗3，按式（8）得2011年的预测值：

3 GM（1,1）模型与灰色马尔柯夫模型预测结果的对比

表6中给出了波动性较大的5个年份的GM（1,1）模型预测与灰色马尔柯夫模型预测值的比较结果。通过对比和分析，不难看出，对于随机波动性较大的原始数据序列，灰色马尔柯夫预测要比灰色GM（1,1）预测具有更高的预测精度。

表6 两种预测方法的比较 %

4 结 语

（1）通过建立的模型，预测2010年我国三级以上建筑工程坍塌事故数为20.6起，而根据已公布的2010年全国建筑生产安全较大事故统计数据显示2010年共发生三级以上建筑安全事故47起，其中坍塌事故19起。所以，预测结果较为满意。

（2）从预测结果来看，2011年三级以上坍塌事故数的预测值高达27起，算得上是近几年中事故高发年份，建设行政主管部门对此应予以重视，积极主动的识别事故风险，采取有效的预防措施来遏制事故多发的势头。

（3）从对我国较大建筑安全事故中的坍塌事故的趋势性分析和预测结果来看，随着近几年我国建筑安全事故呈现下降趋势，全国建筑施工安全生产形势呈现总体稳定好转的时候，较大安全事故中的坍塌事故数却呈现了缓慢上升的趋势。由此，我们得出这样的结论，坍塌事故已经成为制约我国施工安全生产工作的主要事故类型。建设行政主管部门今后的建筑施工安全工作，应将减少和消除坍塌事故作为工作目标之一，制定有针对性的有效地预防和管理措施，以保证建筑施工安全生产工作再上一个新台阶。

[1]刘思峰，党耀国，方志耕，等.灰色系统理论及其应用[M].北京：科学出版社，2004：126-134.

[2]何勇，鲍一丹.灰色马尔柯夫预测模型及其应用[J].系统工程理论与实践,1992（4）：59-63.

[3]蒋承仪.灰色马尔柯夫预测模型[J].重庆建筑大学学报,1996，18(3):116-122.

[4]褚莹.灰色马尔柯夫模型在煤矿安全事故预测中的应用初探[J].能源技术与管理，2006（1）：18-20.

[5]甘旭升,端木景顺,田井远.基于灰色马尔柯夫模型的严重飞行事故频数预测[J].空军工程大学学报，2004，5(1)：18-21.

Application of Grey-Markov Model in the Prediction of Collapse Accident in Construction

LIU Hong-yan1SU Man-man2
(1.Qingdao Oriental Inspection Co.Ltd.，Qingdao 266071;2.Ocean University of China,Qingdao 266100)

This paper presents a thorough study of frequent collapse accident in building construction process,and creates a Grey-Markov forecasting model of collapse accident by combining model GM（1,1）with the forecasting techniques of Markov,and then prejudges the trend and conditions of the collapse accident on the basis of grave collapse accident statistics data.

collapse accident；GM（1,1）model；Grey-Markov model；construction project

TU196:N941

A

1673-1980（2011）06-0150-04

2011-05-12

刘红艳(1968-)，女，山东烟台人，工程师，研究方向为工程管理。