基于无限微元的地表面积求解

基于无限微元的地表面积求解

在信息化条件下，精确打击在作战中具有实际重大的意义。掌握敌方作战的一些具体信息如作战区域地貌信息等能为作战带来巨大便利。文章通过运用无限细分、近似计算的方法将不规则的地表面积的计算简化为三角形的面积计算这一简单过程。具体模型中首先运用数学软件matlab等将目标地形三维图中海拔高于12m的地表取出待用。此外，运用了海伦公式等数学方法来最终达到计算目标地表面积的目的。

地表面积；海伦公式；无限微元

Specific surface area; Helen Formula; infinite subdivision

1 问题重述

某次战斗中，我方拥有详实的敌方作战区域地貌信息。为了更加充分的掌握敌方作战部署，做到在信息化条件下的精确打击，需要在实际中对作战目标的地域进行估算。现在已知该作战区域为长4000m、宽3000m的矩形区域，附件中给出了该区域的步长为5m的网格节点对应的海拔高度值（篇幅所限，具体数值未列），其概貌如图1所示。试通过数学建模方法，估算所给目标区域内的海拔在12m以上部分的地表面积，并分析说明计算精度。

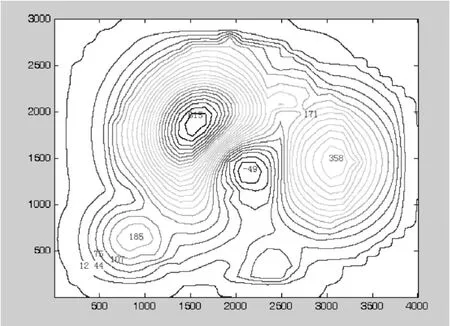
图1 原题附件中的平面投影图

2 符号说明

为简化问题的分析和对数字的处理，下文使用如表1的符号代表变量。

3 问题分析

题目要求建立适当的山地面积计算模型，求解所给目标区域内海拔12m以上部分的地表面积，并分析计算的精度。考虑所给目标区域为一个不规则的山地地形区域，难以直接计算。并且题中所给的数据是长4000m、宽3000m的矩形区域步长为5m的网格节点对应的海拔高度值，联想到微积分求和思想，我们建立了山地面积求解模型。

表1 部分变量符号说明

4 模型建立与求解

4.1 海拔高于12m地表提取

由于目标区域的海拔起伏各异，地形分布不甚规则，且题意要求我们求出海拔高于12m的表面积，故下面先通过一定方法提取目标区域海拔高于12m的地表。具体方法如下：

4.1 采用数学工具matlab做出目标地域的三维地形图如图2所示。

图2 目标地域三维地形图

4.2 提取海拔高于12m的地形部分，海拔低于12m的部分一律归零(如图3所示)；

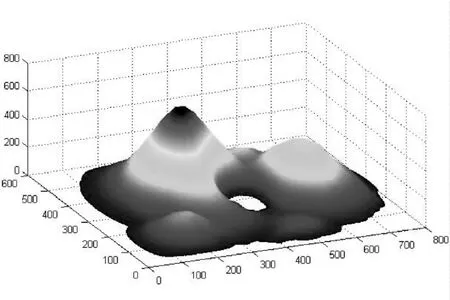
图3 海拔高于12m目标地域三维地形图

4.3 三维地形的表面积求解模型建立

由于三维地形一般是随机起伏的，很难用一个准确的函数来描述这种起伏，所以用传统的数学方法直接计算地表面积具有一定难度，并且难以保证准确度。

对于目标区域，题目所给的数据是长4000m、宽3000m的矩形区域的步长为5m的网格节点对应的海拔高度值，本文以每个网络小格作为面积微元，采用面积微元求和的思想估算目标区域的面积。

分析每个网络小格，假设ABCD四点为相邻的四个点，如图4所示。

图4 山地面积测量

ha、hb、hc、hd分别为四点对应的高度值，lcd、lab分别为CD、AD两点的距离。由已知数据可得：

同理，根据已有数据，得到总共12万个小三角形。

由此可以计算网络小格的面积为两个三角形面积之和为：

S＝2432153.00453477m2

4.4 三维地形的表面积精度分析

由于目标区域的海拔起伏各异，地形分布不甚规则，综合各种因素。我们总结出如下几点肯能引起误差的因素：

①该区域的步长为5m的网格节点对应的海拔高度值不能完全正确的反应地表变化情况；

②模型本身未考虑所选取的最小三角形内部的地形变化；

③计算过程中精度选取不一定达到最大。

我们知道步长越短越精确，而本文给出的最短步长为5m，考虑到通过插值算法得到的更短步长精确性不能检测。本文选择已有数据以10m、15m、20m步长的数据进行精度分析。

通过以10m、15m、20m为步长的程序运行。类似可得到：

10 m 步长时的地表面积：

S＝2333653.80464746m2

15 m 步长时的地表面积：

S＝2135663.32453454m2

20 m 步长时的地表面积：

S＝1834774.12453615m2

进而可以得到逼近准确值的近似曲线。

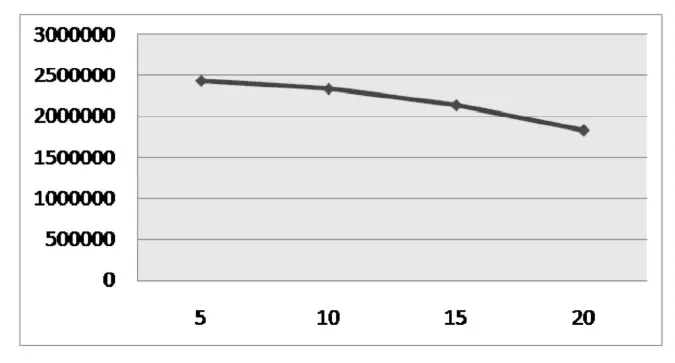
图5 山地面积逼近曲线

由逼近曲线可以近似得到该地型的地表面积标准值接近2500000．我们以此作为标准进行精度分析：

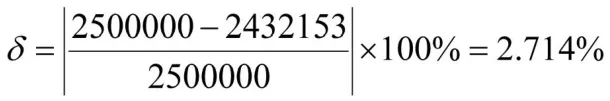
5 结语

本文创新性的将对地表面积的求解转换成对无限微分的最小三角形的面积和求解，使求出的地表面积更加精确可靠．同时，又分别以10m、15m和20m为步长进行精度分析．最后结果误差在3%以内，说明精确度还是很高的。

该模型不仅可应用于军事勘察，同样可用于我们的生活中．如当地震或其他自然灾害发生时，救援人员无法进入灾区，可先通过卫星扫描对该地进行拍照，然后利用该模型对地表情况进行分析，为救援人员提供及时有用的数据。

[1]基于Matlab的地形数据处理.测绘科学与工程第30卷第1期，2010.

[2]魏东，张秀程.基于递归算法的三维地形面积计算方法研究.工程地质计算机应用,2007第3期

An Original Solution to Sompute the Specific Surface area Based on the Theory

of Infinite Subdivision

In the condition of informatization, pintpoint strike has its practical significance.So grasping the information of your enemy’s camp bring a huge convenience for combat operations.In this article,we divide the irregular specific surface into countless tiny triangles with the methods of infinite subdivision and approximate calculation.In the concrete model,first we take out of the surface above 12m in the graphic model with the help of mathematical software matlab2010a .In addition,we calculate the area of each triangle with Helen Formula and the specific surface area is the sum of all triangle areas.

10.3969/j.issn.1001-8972.2011.23.012

吴育文1郭子珑1陈琛2

1 东北大学秦皇岛分校，秦皇岛 066004;2大连交通大学旅顺校区，大连 116001

吴育文（1988-），男，福建长泰人，东北大学秦皇岛分校，在读本科，研究方向：计算数学。