地铁列车气动效应分析

王秀珍 包头铁道职业技术学院

地铁列车气动效应分析

王秀珍 包头铁道职业技术学院

本文基于三维、非定常、可压N-S方程和k-ε双方程湍流模型，对地铁列车以不同速度通过不同截面形状、不同长度隧道引起的气动效应进行了研究。结果表明：地铁列车相同速度通过三种不同截面形状隧道时，圆形截面隧道压力变化幅值最小，马蹄形截面隧道次之，矩形截面隧道最大；列车车体表面压力变化幅值近似与列车运行速度的平方成正比；在此次选择的地铁列车和隧道计算中，最不利隧道长度在2km左右，其最不利隧道长度会因列车运行速度、列车头部外形、隧道截面形状和面积大小等因素不同而有所变化。其结果可为车体气密性和通风设备进排风口位置的设计提供指导意义。

地铁列车；隧道；气动效应；压力变化

引言

与传统的交通工具相比，地铁作为一种轨道交通工具，具有安全、准时、舒适，而且载客量大、运营费用低、环境污染小、综合经济效益等优点，已成为城市交通运输的主力军，大大解决了城市交通堵塞和居民乘车困难等问题，是现代化城市交通运输设备的重要组成部分[1]-[3]。随着城市地铁的迅速发展，地铁环境控制问题也愈来愈引起人们的关注。地铁列车进出隧道、在隧道中运行以及交会时产生很多诸如活塞风、压缩波、膨胀波、噪音等现象，影响乘客和工作人员的舒适性，并会引发安全问题。原来由于地铁列车运行速度较低，地铁列车在隧道中运行时的不舒适感不明显，未引起足够重视，随着地铁列车运行速度的提高，加之地铁列车的气密性不好等原因，瞬变压力通常会给乘客造成耳疼等不舒适感。本文将对地铁列车以不同速度通过不同截面形状隧道时的气动效应进行分析，可为车体气密性和通风设备进排风口位置的设计提供指导意义。

1 数值计算模型

实际流场中，列车上存在扶手、车轮、转向架等，在隧道底板上存在道床、枕木和轨道，流场极其复杂。关注太多细节的复杂流场会大大增加计算工作量，且导致网格畸变甚至计算发散等问题。因此，在现有计算机硬件条件下，为提高流场计算精度，尽可能较细致地模拟地铁列车的外形，但计算模型的网格数不能增加过多，对车体底部和轨道细部结构进行适当简化，计算模型采用三车编组。隧道截面选取三种典型形状截面：圆形、矩形和马蹄形。列车和隧道计算模型如图1所示。

对于边界条件的设置，列车表面给定运动边界条件：X方向速度分量等于给定的列车运行速度V， Y、Z向速度分量等于0；流域两侧面、顶面、底面，给定无滑移边界条件；进口边界条件，相对压强pin＝0；出口边界条件，相对压强pout＝0；隧道壁面采用标准壁面函数模拟。

图1 计算模型图

地铁列车表面压力测点布置如图2所示。

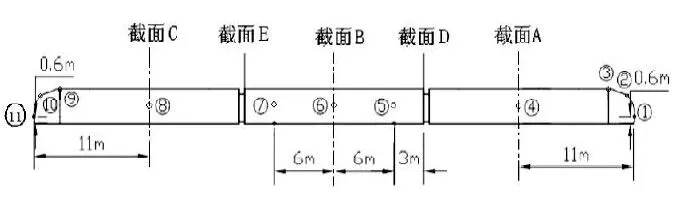
图2 列车车体表面测点布置图

2 数值模拟计算结果与分析

2.1 隧道截面形状对气动效应的影响

图3为列车以80km/h过长度为600m，截面形状为圆形的隧道时车体表面压力分布图（t＝12.5s）。由图可知，列车表面除车头位置处在正压区外，其余位置均为负压。

图3 列车车体表面压力分布云图

列车头、尾部进、出隧道瞬间，绕列车运动的气流受到隧道壁面的制约形成压缩波、膨胀波。这两种波在隧道内以音速传播，当到达另一端洞口时，压缩波突然膨胀转换成膨胀波，而低于环境压力的膨胀波则转换为压缩波，又再以音速回传，如此不断反复传播过程中，同种类型的波相遇叠加时，压力波幅值增大，而不同类型的波叠加时，压力波幅值减小，从而导致隧道内空气压力发生剧烈变化。图4为不同时刻的流场压力分布云图，其中以列车头部距离隧道入口50m时作为计算起始的“零”时刻。t＝1.75s时，由冲击振荡产生的压力波以球面波的形状向外传播；t=2.5s时，列车头部进入隧道，在隧道入口附近的压力开始上升，随着列车头部继续接近并进入隧道，压力继续升高形成压缩波；t=5.0s时，列车尾部进入隧道，形成膨胀波，压力开始下降。

图4 纵向对称面压力分布云图

图5为地铁列车以80km/h通过三种不同截面形状隧道时，车体表面6#点的压力随时间变化历程，结果表明列车以相同速度通过圆形截面隧道时车体表面压力变化幅值最小，马蹄形隧道次之，矩形截面隧道最大；除压力变化幅值有些差异外，曲线变化规律完全一致，其他测点压力变化结果类似，这里不再详细分析。

图5 通过不同截面形状隧道时6#测点压力变化曲线

从测点压力变化值和压力变化曲线可知，地铁列车在隧道中运行时，除列车头部处于微小正压区外，大部分区域均为负压，这对出风有利，对进风不利；地铁列车以80km/h运行时，除车头外，车体表面其它位置测点压力变化范围在200Pa至-600Pa之间，平均负压大概为-300Pa；在设计空调等通风设备进排风口时，需要考虑车体表面压力分布情况。

2.2 列车运行速度对气动效应的影响

这里取地铁列车中间车厢侧面6#测点进行分析比较。地铁列车以60km/h、80km/ h和100km/h速度通过长600m的圆形截面隧道时的车体表面压力计算结果如表1所示，测点压力变化历程如图6所示，根据表1中数据画出的列车表面测点压力变化幅值与列车速度的关系曲线如图7所示。从计算结果可知，随着地铁列车运行速度的提高，列车车体表面压力变化迅速增大，列车车体表面压力变化幅值近似与列车运行速度的平方成正比。

表1 不同速度通过圆形截面隧道时车体表面6#测点压力变化情况

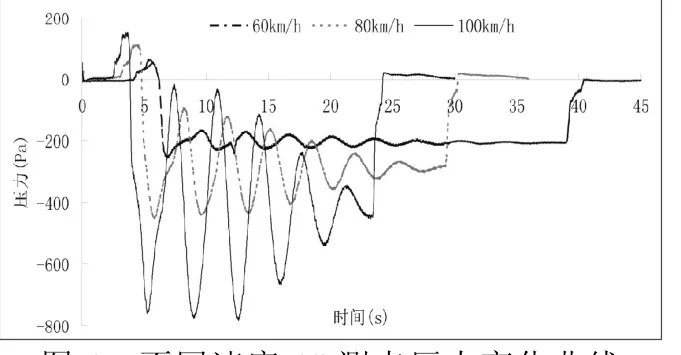
图6 不同速度6#测点压力变化曲线

图7 6#测点压力变化幅值随车速变化曲线

2.3 隧道长度对气动效应的影响

列车以80km/h的速度分别通过长度为350m、600m、1000m、1500m、2000m、3000m的圆形截面隧道时，取列车中间车厢侧面6#测点的压力数据进行分析比较。测点压力变化情况如图8所示，列车表面压力变化幅值与隧道长度的关系曲线如图9所示。

图8 列车通过不同隧道长度时6#测点压力变化曲线

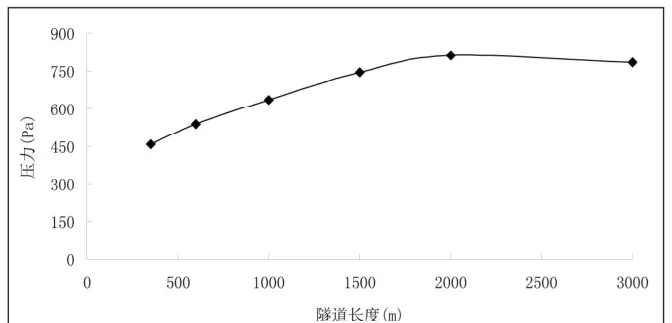
图96 #测点压力变化幅值随隧道长度变化曲线

由图9可知，列车过长度为350m的隧道时压力变化幅值最小，为458pa；随着隧道长度的增加，列车车体表面压力变化幅值迅速增加，在2000m左右达到最大，为812Pa；然后随着隧道长度的增加，列车车体表面压力变化幅值慢慢减小。可见，此次计算的隧道最不利长度约为2000m，当然最不利隧道长度还与列车运行速度、列车头部外形、隧道截面形状和面积大小等因素有关，要针对具体问题进行分析。

3 结论

通过对地铁列车通过隧道的气动效应进行分析，可以得到以下结论：

（1）地铁列车在隧道中运行过程中，除列车头部处于微小正压区外，大部分区域均为负压，这对出风有利，对进风不利；地铁列车以80km/h运行时，除列车头、尾个别测点外，车体表面其它位置测点压力变化范围约在200Pa至-500Pa之间，平均负压大概为-300Pa。

（2）列车以相同速度通过圆形截面隧道时车体表面压力变化幅值最小，马蹄形截面隧道次之，矩形截面隧道最大。三种不同截面形状的隧道基本相同，除测点压力变化幅值有些差异外，曲线变化规律完全一致。

（3）随着列车运行速度的提高，车体表面压力变化幅值增大，列车车体表面压力变化幅值近似与列车运行速度的平方成正比。

（4）隧道长度在350m～2000m范围内，随着隧道长度的增加，列车车体表面压力变化幅值增大，隧道长度大于2000m后，随着隧道长度的增加，列车车体表面压力变化幅值慢慢减小；可见，此次计算的隧道最不利长度约为2000m，最不利隧道长度会因列车运行速度、列车头部外形、隧道截面形状和面积大小等因素不同而有所变化，要针对具体问题进行分析。

[1]王元.香港地铁发展模式对北京的启示[D].北京：北京交通大学.2006

[2]曹炳坤.世界地铁发展令人瞩目[J].城市公共交通.2003，23(5)：33

[3]余斌.城际快速地铁线空气动力学效应与隧道规模[J].商品与质量·建筑与发展.2010，23(9)：118-120

[4]贾力，黄鹏，李时娟.地铁双线隧道内流动特性的数值模拟[J].热科学与技术.2006，5(4)：332-334

[5]刘堂红，田红旗，金学松.隧道空气动力学实车试验研究[J].空气动力学学报.2008，26(1)：42-46

[6]刘艳荣，毛军.列车活塞风对隧道通风系统运行状态的影响[J].工程建设与设计.2003，(4)：3-6

U121

A

10.3969/j.issn.1001-8972.2011.21.045