超强磁场下非掺杂ZnSe/BeTeⅡ型量子阱中激子和带电激子的光学特性*

冀子武 郑雨军 徐现刚

1)(山东大学物理学院，济南 250100)2)(山东大学晶体材料国家重点实验室，济南 250100)(2009年11月14日收到;2010年7月25日收到修改稿)

超强磁场下非掺杂ZnSe/BeTeⅡ型量子阱中激子和带电激子的光学特性*

冀子武1)郑雨军1)徐现刚2)

1)(山东大学物理学院，济南 250100)2)(山东大学晶体材料国家重点实验室，济南 250100)(2009年11月14日收到;2010年7月25日收到修改稿)

报道了液态氦温度(4.2 K)下非掺杂ZnSe/BeTeⅡ型量子结构中ZnSe势阱层内空间直接光致发光(PL)光谱的磁场依赖性(磁场高达53 T).实验结果显示，随着磁场的增加，激子和带电激子的PL强度呈现出相反的振动行为.当激子的PL强度增加时带电激子的PL强度减小，反之，当激子的强度减小时带电激子的强度却增加.并且在整个磁场范围内，这些振动呈现近似等间隔的周期性变化.这个行为被解释为费米能级与朗道能级的周期性共振，这个共振导致了处于费米能级上的二维电子气态密度的周期性调制.

光致发光，二维电子气，带电激子，Ⅱ型量子阱

PACS:78.55.－ m，71.10.Ca，71.35.Pq，73.21.Fg，78.20.Ls

1.引 言

近年来，随着分子束外延 (MBE)生长设备与技术的日益完善和成熟，使得制作超低维、低晶格失配、低无意掺杂浓度的高质量化合物半导体异质结构成为可能［1—3］.ZnSe/BeTe作为一种新型的Ⅱ-Ⅵ族异质结构已经显示了许多新的特性.其Ⅱ型能带结构和较大的导带(或价带)边能量落差△ECB(或△EVB)，使得势阱层ZnSe中受激产生的电子和孔穴发生空间分离，电子被限制在原来的 ZnSe层内，而空穴则逃逸到相邻的能量更低的 BeTe层中［3—8］.这种空间分离所造成的 ZnSe层中电子和孔穴浓度的失衡，使得我们即使在非掺杂的结构中也能够在光致发光(PL)光谱中同时观察到激子(X)和带电激子 (X－)的存在［9，10］. 因此，ZnSe/BeTeⅡ型量子阱(QW)是研究低维半导体中各种光学过程，特别是高密度凝聚现象的理想结构.

在极限实验条件下测试、研究低维系统的各种光学行为，是理解、掌握其内部动力学过程的重要手段之一.作为极限条件之一的超强磁场，已经在研究ZnSe/BeTeⅡ型QW等结构的光学特性中发挥了重要的作用［4］.如在超强磁场下，通过回旋共振(cyclotron-resonance)测量已获得阱层(ZnSe)中电子的浓度、有效质量、散射时间及迁移率等重要信息;而在空间间接PL测量中，已观察到多体相互作用(many-body interaction)的新型行为等.然而，在超强磁场条件下，对于ZnSe/BeTeⅡ型QW结构中X和X－共存的空间直接PL跃迁行为的研究，据我们所知，迄今为止还没有详细的报道.解明X和X－对强磁场的不同相应机制，对于丰富凝聚态理论，开发新型的光电器件(如磁控开关、磁触发器件等)都具有重要意义.

为了探明ZnSe/BeTeⅡ型QW结构的空间直接PL跃迁的内部物理机理，本文设计并制作了非掺杂、非对称的ZnSe/BeTe/ZnSeⅡ型 QW 结构，并测试了该结构在极低温(4.2 K)条件下PL光谱的磁场(磁场高达53 T)依赖性.我们发现了PL谱在X和X－共存情况下的磁场变化行为，并详细解释了X和X－之间的内在关联和转换机理.

2.样品结构及实验方法

本研究所用的ZnSe/BeTe/ZnSe样品是作者在日本千叶大学留学期间于日本国家产业技术综合研究所(AIST)超高速光学器件研究室(UPDL)用分子束外延(MBE)的方法，在(001)GaAs衬底上生长而成的［4，5］. 非对称非掺杂的 ZnSe(40 ML)/BeTe(10 ML)/ZnSe(28 ML)QW结构被夹在两个200 nm厚的Zn0.77Mg0.15Be0.08Se隔离层之间(ML:monolayer，单分子层).有关本样品的生长过程和其他结构参数请参阅文献［3—5］.

图1 不同磁场时的光谱(实线为实验结果，虚线分别表示X和X－在光谱中的分量，空心圆表示它们的和)

上述样品的磁性 PL(magneto-PL)测量是作者作为研究员在日本东京大学物性研究所国际超强磁场研究中心工作期间进行的.所用的脉冲磁场(高达53 T)是通过电容器放电产生的.磁场的方向与量子阱的生长方向相同(即，法拉弟配置).一个连续波(cw)He-Cd激光器(325 nm)被用作激发光源.样品表面的激发密度为P=10 W/cm2.上述光谱测量是在低温(液态氦温度，4.2 K)下进行的.信号检测使用了ANDOR TECHNOLOGY公司的ICCD探测器.

3.实验结果与讨论

图1分别显示了连续变化磁场(0—53 T)中相应于0，26，和53 T时样品结构中 ZnSe层的空间直接PL谱的情形.测量温度 T=4.2 K，激发密度 P=10 W/cm2.在零磁场时(如图1(a)所示)，峰值处在能量为2.815 eV的发光峰为40 ML ZnSe层的X跃迁，而位于该发光峰的低能端约6 meV处的较强的发光峰为 X－的跃迁［9，10］. 然而，来自 20 ML ZnSe层的跃迁却没有被观察到，这是由于该层的厚度太窄所致［9—12］.为了调查 X和X－的发光强度和峰值能量随磁场的变化规律，对整个磁场范围内的所有PL谱我们用双 Voigt线型(double voigt line-shape)函数进行了反卷积［10，13］.图 1显示了磁场强度为0，26和53 T时的拟合结果.其中，实线表示实验结果，虚线分别表示分离的X和X－的发光峰，而空心圆则代表它们的和.图2显示了X和X－的PL强度和峰值能量在整个磁场范围内(0—53 T)对磁场B的依赖性.

如图2所示，当 B大于约12 T时，X－的 PL强度IX－和峰值能量 EX－显示了一个明显的振动行为.然而，对于X，我们只观察到了其 PL强度 IX的振动行为.同时还发现，在X和X－的PL强度之间存在着一个明显的竞争行为.即，当 IX－减小时 IX增加，反之，当IX－增加时IX减小.类似的振动行为在其他样品(如对称结构的 ZnSe/BeTe/ZnSeⅡ型量子阱)的实验测量中也已经被观察到.上述振动行为被认为是与 光生(photo-excited)空穴和处在费米能级上的电子有关.在磁场存在的情况下，二维电子气(2DEG)系统的费米面总是处在被电子占有的最高朗道能级(Landau level)上(如图3所示).根据公式NL=eB/h(NL为每个朗道能级上的态密度，e电子的电量，h为普朗克常数)，随着 B的增加，每个朗道能级上的态密度也增加.因为激发强度是恒定的(P=10 W/cm2)，所以一般来说电子的浓度(Ne)应近似为常数.基于上述分析，随着B的增加，当被电子占有的最高朗道能级变为全空时，费米面就会移动到下一个较低的朗道能级上.这样，朗道能级与费米面的周期性共振导致了2DEG系统态密度的周期性调制.当2DEG的浓度增加时，IX－增加，同时，由于来自电子的屏蔽作用也相应增强，结果导致IX减小，反之亦然.因此，在连续变化的磁场中，IX－和IX的上述竞争行为被认为是起因于由费米面与朗道能级周期性共振造成的2DEG浓度的周期性变化.EX－的振动主要是起因于2DEG系统费米面的起伏(如图2(b)所示).

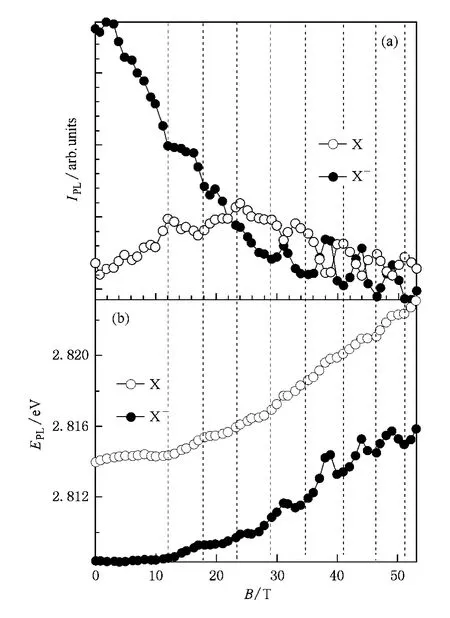
图2 X和X－的PL积分强度(a)和峰值能量(b)与磁场的关系(竖直虚线显示了IX－极小值和IX极大值所处的磁场位置)(a)IPL-B;(b)EPL-B

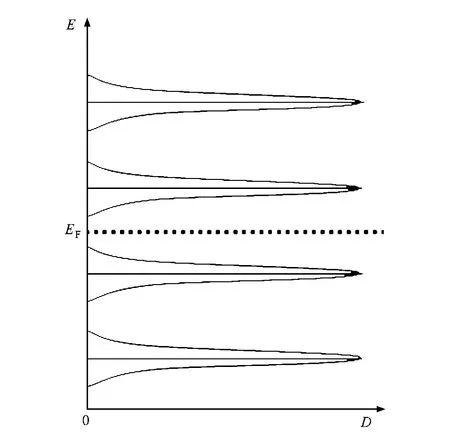
图3 朗道能级与态密度关系示意图.其中，E，D和EF分别表示能量，态密度和费米面

我们也注意到，在整个磁场范围内，本实验所用样品以及其他相近样品都展示了一个类似的变化行为，即，IX－展示了一个显著的降低，同时EX－和EX则显示了一个非线性增加(如图2(a)所示).前者是由磁场产生的有效限制(effective confinement)导致X－的相干体积 (coherence volume)减小造成的［14］，而后者则是起因于激子的反磁性位移(excitonic diamagnetic shift).另外，我们还发现，IX－，IX及EX－的这些振动所产生的极大值(或极小值)对于B来说几乎是等间隔的(如图2中的竖直虚线所示).综合其他样品的实验结果，我们发现这个振动间隔一般来说是非规则的，并与多种因素有关(如，样品结构，实验温度，激发强度等).这个非规则的振动间隔反映了在磁场变化过程中，结构内的电子浓度并不是一个恒量，因此我们无法根据公式ν=Neh/eB来求解填充因子ν.这可能是强磁场下的一个独特现象，即在连续变化的强磁场中，该结构中的电子浓度随磁场的变化有一定的起伏.我们先前的有关该类结构的Ⅱ型PL研究成果也支持这一观点［15—17］.这一点不同于其它的一些研究报道，如，Lema tre［18］，Yamashita［19］，Nomura［20］等人的研究报道.因为这些报道所涉及的都是低磁场范围(一般小于7 T，最大也不会超过12 T)下的光学行为，在这种情况下，电子浓度可以被看作是一个常数，所以可以用公式ν=Neh/eB来求解填充因子.当然，要完全探明、解释该结构中的各种光学现象，还有待于进一步的理论和实验探讨.

4.结 论

本文在极低温、超强磁场条件下调查了非对称、非掺杂ZnSe/BeTe/ZnSeⅡ型QW结构的空间直接PL跃迁的光谱特性.结果发现，X和X－共存的PL光谱在连续变化的磁场中展示了一个有趣的振荡行为:当IX增强时 IX－则减小，反之，当 IX减小时IX－则增强.这个竞争行为被解释为起因于朗道能级与费米面的周期性共振，这个共振导致了2DEG浓度的周期性调制.当2DEG浓度增加时，IX－增加，同时X因受到来自电子的屏蔽增加而导致其强度IX减小，反之亦然.EX－的振动行为反映了费米面随变化磁场的起伏过程.

感谢日本千叶大学光物性量子传导研究室的各位老师在数据处理、理论分析过程中所给予的大力支持和帮助.

［1］ Song Y X，Zhang W M，Liu J，Chu N N，Li S M 2009 Acta Phys.Sin.58 6471(in Chinese)［宋迎新、郑卫民、刘 静、初宁宁、李素梅 2009物理学报 58 6471］

［2］ Cai C F，Wu H Z，Si J X，Sun Y，Dai N 2009 Acta Phys.Sin.58 3560(in Chinese)［蔡春锋、吴惠桢、斯剑霄、孙 艳、戴宁2009物理学报 58 3560］

［3］ Ji Z W，Lu Y，Chen J X，Mino H，Akimoto R，Takeyama S 2008 Acta Phys.Sin.57 1214(in Chinese)［冀子武、鲁 云、陈锦祥、三野弘文、秋本良一、嶽山正二郎 2008物理学报 57 1214］

［4］ Ji Z W，Mino H，Oto K，Akimoto R，Ono K，Takeyama S 2006 Semicond.Sci.Technol.21 87

［5］ Ji Z W，Yamamoto H，Mino H，Akimoto R，Takeyama S 2004 Physica E 22 632

［6］ Ji Z W，Mino H，Kojima E，Akimoto R，Takeyama S 2008 Acta Phys.Sin.57 3260(in Chinese)［冀子武、三野弘文、小映二、秋本良一、嶽山正二郎2008物理学报57 3260］

［7］ Ji Z W，Mino H，Oto K，Muro K，Akimoto R，Takeyama S 2008 Acta Phys.Sin.57 6609(in Chinese)［冀子武、三野弘文、音贤一、室清文、秋本良一、嶽山正二郎 2008物理学报57 6609］

［8］ Mino H，Fujikawa A，Akimoto R，Takeyama S 2004 Physica E 22 640

［9］ Ji Z W，Takeyama S，Mino H，Oto K，Muro K，Akimoto R 2008 Appl.Phys.Lett.92 093107

［10］ Ji Z W，Mino H，Oto K，Akimoto R 2009 Semicond.Sci.Technol.24 095016

［11］ Maksimov A.A，Tartakovskii I I，Yakovlev D R，Bayer M，Waag A 2006 JETP Lett.83 141

［12］ Haetty J，Lee E H，Luo H，Petrou A，Warnock J 1998 Solid State Commun.108 205

［13］ Manassen A，Cohen E，Ron Arza，Linder E，Pfeiffer L N 1996 Phys.Rev.B 54 10609

［14］ Homburg O，Sebald K，Michler P，Gutowski J，Wenisch H，Hommel D 2000 Phys.Rev.B 62 7413

［15］ Ji Z W，Enya Y，Mino H，Oto K，Muro K，Akimoto R，Takeyama S 2006 J.Phys:Conf.Seri.51 427

［16］ Ji Z W，Mino H，Oto K，Akimoto R，Ono K，Takeyama S 2006 Semicond.Sci.Technol.21 87

［17］ Enyal Y H 2007 Graduate School of Engineering Faculty of Engneering，the University of Tokyo Master Paper p116(in Chinese)［塩谷陽平2007東京大学大学院工学系研究科物理工学专攻硕士论文 p116］

［18］ Lema tre A，Testelin C，Rigaux C，Wojtowicz T，Karczewski G 2000 Phys.Rev.B 62 5059

［19］ Yamashita K，Kita T，Matsuura Y，Wada O，Geng C，Scholz F，Schweizer H，Oe K 2002 Phys.Rev.B 66 195317

［20］ Nomura S，Nakanishi T，Aoyagi Y 2001 Phys.Rev.B 63 165330

PACS:78.55.－ m，71.10.Ca，71.35.Pq，73.21.Fg，78.20.Ls

Optical properties of exciton and charged exciton in undoped ZnSe/BeTe type-Ⅱquantum wells under high magnetic fields*

Ji Zi-Wu1)Zheng Yu-Jun1)Xu Xian-Gang2)
1)(School of Physics，Shandong University，Jinan 250100，China)2)(State Key Laboratory of Crystal Materials，Shandong University，Jinan 250100，China)(Received 14 November 2009;revised manuscript received 25 July 2010)

We report on the magnetic field(up to 53 T)dependence of photoluminescence(PL)spectra occurring as a spacially direct optical transition of the ZnSe layer in undoped ZnSe/BeTe/ZnSe type-II quantum structures at a low temperature(4.2 K).With magnetic field increasing，the PL intensity(IX)of exciton(X)shows an oscillation feature opposite to the PL intensity(IX－)of charged exciton(X－).As IX－

increases，IXdecreases，but as IX－

decreases，IXincreases.In all fields，the oscillation behaviour shows a periodic change approximately with magnetic field interval.The results are attributed to the periodic resonance of the Fermi level with the Landau level，which results in the modulation of the density of states of the 2DEG system at the Fermi energy.

luminescence，two-dimensional electron gas，charged exciton，type-Ⅱ quantum well

*国家自然科学基金(批准号:10844003，10874101)，山东省自然科学基金(批准号:Y2008A10)，国家重点基础研究发展计划(批准号:2009CB930503)资助的课题.

E-mail:jiziwu@gmail.com

*Project supported by the National Natural Science Foundation of China(Grant Nos.1084403，10874101)，the Shandong Nataral Science Foundation of China(Grant No.Y2008A10)，the National Basic Research Program of China(Grant No.2009CB30503).

E-mail:jiziwu@gmail.com