基于改进粒子群优化算法的物流配送中心选址技术

胡 琳

(湖南工程学院 经济管理学院，湖南 湘潭 411104)

基于改进粒子群优化算法的物流配送中心选址技术

胡 琳

(湖南工程学院 经济管理学院，湖南 湘潭 411104)

文章同时考虑客户和物流规划部门的利益，构建了物流配送中心地址优化的双层规划模型。提出了一种改进的粒子群优化算法，分别求解双层规划模型的上层模型和下层模型。仿真实例表明了本文方法的可行性和有效性。

双层规划模型；粒子群优化算法；选址；物流配送中心

0 引言

物流配送中心选址是诸多管理决策问题之一。无论是分配系统的成本还是客户服务水平都显著地取决于配送中心的数量、规模和位置以及每个中心所服务的客户。因此，大量研究一直致力于物流配送中心选址的数学模型。

物流配送中心选址问题能作为领导者-跟随者模型或斯塔克尔贝格游戏的一个代表，决策管理者是领导者，客户就是那些可自由选择配送中心的跟随者。因此，用双层规划模型来表现选址问题是恰当的。然而，尽管已经广泛地研究了设施选址问题，仍然只有极少数关注使用双层规划模型。谷口未央[1]发展了一种双层模型来决定公共物流终端的最佳规模和地点。模型上层描述了规划者最大化降低整体成本的行为，成本包括了运输成本(长途运输与提取运送费用)和设施投资成本。模型的下层则用来决定在任意公共物流终端的卡车和客车的平衡分配。该模型直接采取遗传算法进行求解。尽管如此，客户需求分配(响应功能形式)地点位置的影响并没有分析得很精准。双层模型精确的响应功能(上层模型变量与下层模型变量的变动关系)是至关重要的。鉴于此，本文同时考虑客户和物流规划部门的利益，构建了物流配送中心地址优化的双层规划模型。提出了一种改进的粒子群优化算法，分别求解双层规划模型的上层模型和下层模型。仿真实例表明了本文方法的可行性和有效性。

1 物流配送中心选址模型

与传统单层规划模型相比，双层规划模型具备更多优点：(1)双层规划模型能在决策过程中同时分析两种不同甚至是冲突的客观事物；(2)双层规划模型的多重准则可更好地反映出实际问题；(3)双层规划模型能明确地代表系统管理者与客户的共同行为。由于物流配送中心的选址问题涉及到系统管理者和客户这两种类型的决策者，有着不同的目标函数，显然，采用双层规划模型来描述选址问题是恰如其分的。

1.1 物流配送中心选址的上层模型

物流配送中心选址的上层模型主要用来决定配送中心的最优场所从而使得整体成本(固定和变动费用)最小，在决策者制定的固定投资范围内来满足位于不同位置的客户需求。假定在建新配送中心之前没有任何配送中心，即不需要考虑新旧配送中心之间的竞争。物流配送中心选址的上层规划模型描述如下：

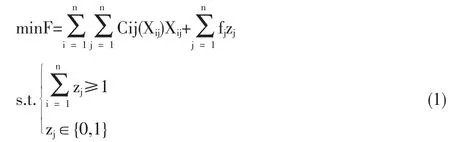
这里，Cij(Xij)表示配送中心j满足客户需求的整体成本，通常是一个非线性函数；Xij表示由配送中心j提供给客户的物资；fj表示与建造配送中心相关联的固定投资；zj表示0～1变量，如果配送中心j已建好，那么zj就是1，反之为0。

从决策者的角度来看，上层模型目标函数的第一部分表示了满足客户需求的整体变动成本，第二部分表示了与建造配送中心相关联的固定成本。固定投资成本包括土地征用费用和设施建造费用。第1个约束确保了至少建造一个配送中心，第2个约束表示了决定变动的双重限制。物流配送中心选址的上层模型是非线性的0～1整数规划问题。

1.2 物流配送中心选址的下层模型

在物流配送系统中，某个客户的需求分配受到其他客户需求分配的影响。假如所有客户都去一个配送中心(根据交通费用这可能是最近的)，由于整体需求费用的独立性，可能将发展为拥挤。因此，该地点的成本增加到一定程度可能不再是费用最小的那个。一些客户可能将选择别的配送中心，这个配送中心也有可能拥挤。这个过程就需要重复分配直到达到一种平衡状态。在这种状态下，所有使用的配送中心费用将持平，并且也小于或等于到任意非配送中心的费用，这种平衡称为用户均衡状态。为了反映这种现象，采用需求函数来描述客户和客户j的最低成本与客户分配的关系。

Xij=Dij(uij),坌i=1,2,…，m，j=1,2,…，n

这里，uij表示从配送中心j满足客户i需求的最低成本，D(·)表示最低成本uij的单调递减函数，它反映了配送规模、服务等级和成本信息等。物流配送中心选址的下层模型如下所示：

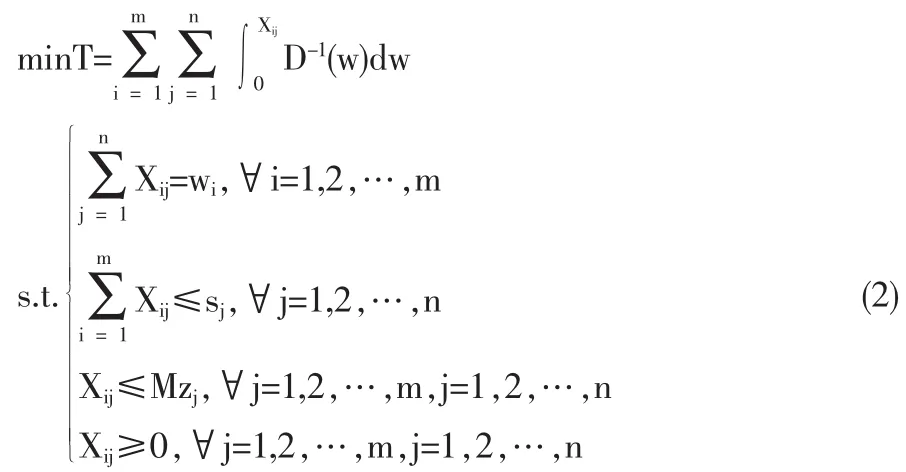
这里，D-1（·）表示需求函数的反函数，需求函数的反函数的常见形式是幂函数和对数函数；wi是客户i的整体需求，sj是配送中心j的容量；M是一种任意的大的正常数。

物流配送中心选址的下层模型代表了客户选择行为和分配在各配送中心的需要，也就是说，每个客户把他的需求分配到各配送中心以最大化降低他的总费用。在物流配送中心选址的下层模型中，第一个约束确保每位客户的总需求由一些配送中心来提供满足；第二个约束是容量约束，确保所有分配到每个配送中心的需求不会超过它的容量；第三个约束禁止在实际上并未修建的配送中心提供需求，M是一种任意的大的正常数，如果zj=0，那么Xij不可能是正数；如果zj=1，那么Xij可尽可能地大；第四个约束代表决策变量的非负限制。

2 改进粒子群优化算法

粒子群优化算法(Particle swarm optimization，PSO)以鸟群的集体协作为寻优目的，主要模拟鸟群飞行觅食行为。在PSO算法中，自身、历史最优位置和整个粒子群的全局最优位置给每个粒子提供信息，单个粒子在方案空间内不断飞行，从而达到实现寻找最优解的目的。尽管有关离散域，尤其是路由规划和组合优化问题研究得较少，但是粒子群优化算法已成功地应用于求解连续问题。就TSP问题而言，Clere等提出了一个具体的DPSO算法。虽然未考虑到离散量运算规律的不同，跟其他算法存在着不小的差距，但其定义速度为交换列表，也定义了其他量及运算法则。同样，利用交换列表的规律，黄岚等也定义了不同的离散量运算规则，算法仅仅针对小维数TSP问题进行了仿真。尽管如此，他的算法证明了PSO在求解离散优化问题是可行的，仍然显现了其极强的进化特征。

2.1 位置与速度的加法运算

粒子位置的变化由位置与速度加法运算来体现，可由以下公式来确定新位置。其中交换位置x中的xi和vi由函数来定义。如新位置(5,2,3,1,4)由=(0,2,3,0,4)和=(2,4,5,1,3)得到。

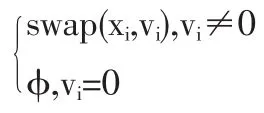
2.2 位置的减法运算

1个速度由两位置相减所得，下式可用来表示v=x2-x1位置减法运算的含义。

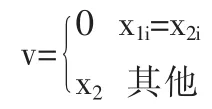
2.3 速度的数乘运算

我们定义v=c1vc2(1≤c1,c2≤N)，把1到N的循环列表看成是维，从位置开始进行左乘的操作，右乘c2表示至c2-1位置结束。维的速度在这之间取原有值，其余位置值都为0。随机产生的数值即c1和c2(c2>c1)。c2=c2-length(v)时意味着c1为速度的最后一维数据。从而得到较为均衡的粒子速度，并且它向最佳方向的飞行也很均衡。同时，参数c选取所带来的问题也随即消失了，下列公式也可表示速度的数乘运算规则。

2.4 速度的加法运算

1个新的速度由2个速度相加获得，v=v1+v2，其中分量定义为：

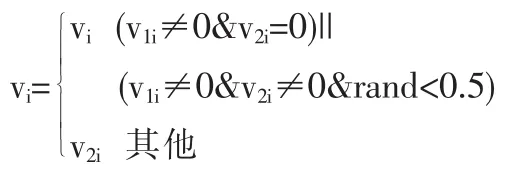
2.5 改进的粒子运动方程

站在社会心理学的角度，个体学习自身成功行为的能力由学习因子C1来表示，这个同时也称为认知因子，而C2即为社会因子，代表了学习社会成功行为的能力。以Pgt和Plt为中心的领域所有范围都能由C1和C2搜索到。在本文中，搜索效果再次受到每次迭代过程中每代的最优值PCT的影响。C3定义为时代因子，表示学习本次迭代成功行为的能力。实现这一方法主要在于进一步改进的粒子运动方程，并且将1个当前代粒子最优位置Pct重新定义，这样不仅能使粒子向个体最优和全局最优靠拢，而且还能向当前代的最优值靠近。鉴于DPSO的特殊性，采用分段计算方式将达到更好的效果，原因在于对位置上各维数据的作用是相互的。

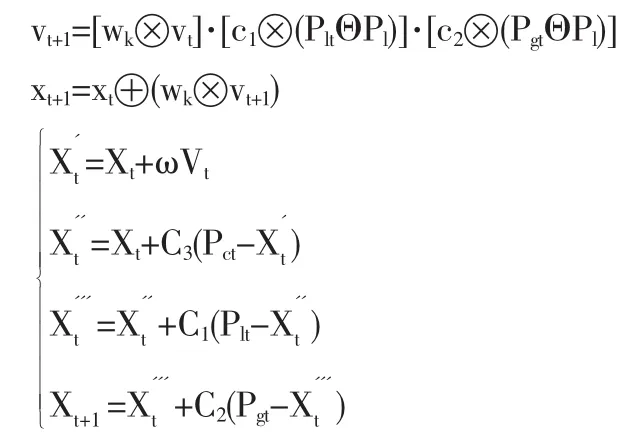
3 仿真实例

本部分通过一个简单的数值例子来描述模型以及验证本文方法的正确性。虽然数值例子的说服力有点微弱，应该从客户的实际行为观察证实，但这个例子重点用来验证本文方法的正确性。假定系统中有一个客户，有四个候选的配送中心位置(B1,B2,B3,B4,B5,B6,B7,B8,B9)，整体成本函数为：

Cij(Xij)=aij(Xij)bij-Eij

客户需求w1=400，需求的反函数如下：

D-1(Xij)=aij(Xij)bij-Vij

其中aij,bij,Eij和Vij都是参数。假设：

a11=0.15，a12=0.08,a13=0.1,a14=0.07,a15=0.08,a16=0.1,a17=0.07,a18=0.08,a19=0.1,

b11=0.33，b12=0.33,b13=0.33,b14=0.33,b15=0.33,b16=0.33,b17=0.33,

b18=0.33,b19=0.33,

E11=0.8z，E12=1.7z2,E13=1.5,E14=1.2z4,E15=1.7z5,E16=0.51z6,E17=1.2z7,E18=1.7z8,E19=0.51z9,

f1=1,f2=0.7,f3=1.5,f4=0.9,f5=0.7,f6=1.5,f7=0.9,f8=0.7,f9=1.5

再假定配送容量是无穷大的，M=500，e=0.05。

根据第三部分的改进粒子群优化算法，求得的物流配送中心选址的下层模型的最优方案为：

X*=(0,0,0,0,0,0,0,0,400)

反应函数分别如下所示：

X11=400z1-400

X12=400z2-400

X13=400z3-400

X14=400z4-400

X15=400z5-400

X16=400z6-400

X17=400z7-400

X18=400z8-400

X19=400z9

再根据第三部分的改进粒子群优化算法，求得的物流配送中心选址的上层模型的最优方案为：

z1=0,z2=0,z3=0,z4=0,z5=0,z6=0,z7=0,z8=0,z9=1

即最后的配送中心应该建造，其他的不应该建造。配送中心的客户需求分布为：

X11=0,X12=0,X13=0,X14=0,X15=0,X16=0,X17=0,X18=0,X19=400

4 结束语

物流配送中心选址是诸多管理决策问题之一。无论是分配系统的成本还是客户服务水平都显著地取决于配送中心的数量、规模和位置以及每个中心所服务的客户。

本文同时考虑客户和物流规划部门的利益，构建了物流配送中心地址优化的双层规划模型。物流配送中心选址的上层模型主要用来决定配送中心的最优场所从而使得整体成本(固定和变动费用)最小，在决策者制定的固定投资范围内来满足位于不同位置的客户需求。物流配送中心选址的下层模型代表了客户选择行为和分配在各配送中心的需要，也就是说，每个客户把他的需求分配到各配送中心以最大化降低他的总费用。

粒子群优化算法(Particle swarm optimization，PSO)以鸟群的集体协作为寻优目的，主要模拟鸟群飞行觅食行为。提出了一种改进的粒子群优化算法，分别求解双层规划模型的上层模型和下层模型。仿真实例表明了本文方法的可行性和有效性。

[1]E.Taniguchi.Optimal Size and Location Planning of Public Logistics Terminals[J].Transport.Res.,1999,35(3).

[2]C.H.Aikens.Facility Location Models for Distribution Planning[J].Eur.J.Oper.Res,1985,(22).

[3]K.Holmberg.Exact Solution Methods for Uncapacitated Location Problem with Convex Transportation Costs[J].Eur.J.Oper.Res,1999,(114).

[4]F.Barahona,D.Jensen.Plant Location with Minimum Inventory[J].Math.Program,1998,(83).

[5]S.H.Owen,M.S.Daskin.Strategic Facility Location:a Review[J].Eur.J.Oper.Res.,1998,(111).

[6]A.Klose,A.Drexl.Facility Location Models for Distribution System Design[J].Eur.J.Oper.Res.,2005,(162).

[7]G.Zhou,H.Min,M.Gen.The Balanced Allocation of Customers to Multiple Distribution Centers in the Supply Chain Network:a Genetic Algorithm Approach,Comput.Ind.Eng.,2002,(43).

[8]S.S.Syam.A Model and Methodologies for the Location Problem with Logistical Components[J].Comput.Oper.Res.,2002,(29).

[9]Z.Q.Lu,N.Bostel.A Facility Location Model for Logistics Systems Including Reverse Flows:the Case of Remanufacturing Activities[J].Comput.Oper.Res.,2007,(34).

F252

A

1002－6487（2011）04－0057-03

胡 琳（1969-），女，湖南湘乡人，硕士，讲师，研究方向：物流管理。

（责任编辑/亦 民）