ZGMn13高锰钢本构方程及仿真实验的研究*

许立藤涛杨亮李波

（大连交通大学机械工程学院，辽宁大连 116028）

材料的本构方程是用来描述应力、应变、应变率、 温度、应变历史的关系方程。金属切削加工的数值仿真结果是否能反映实际加工的情况在很大程度上取决于本构方程的建立，所以建立精确的材料模型在有限元仿真中具有重要的意义［1－3］。以前人们对本构方程的研究主要集中在普通低、中碳钢上，还没有对高锰钢的材料性能进行过研究。

通过做ZGMn13高锰钢的压缩实验和分离式Hopkinson压杆实验，对其在常温、不同时效处理下的材料试验的结果进行分析处理，拟合出材料Johnson－Cook本构方程。

1 试验设计及方法

试样材质为ZGMn13高锰钢并将其加工成11.30 mm×11.16 mm×24.47 mm的长方体和φ4 mm×4 mm的圆柱体用以完成压缩试验和压杆试验。所用的设备是金属压缩试验机和Split Hop－kinson Pressure Bar压杆装置。压缩试验的加载速度为5 mm/min;10 mm/min。材料种类为原始高锰钢试样;400时效高锰钢试样;500时效高锰钢试样;600时效高锰钢试样。

2 静态压缩试验和Hopkinson压杆试验

2．1 压缩试验的数据

在每一组应变率下测试4个试样，测量的结果为4个试样值的平均值。应变率为

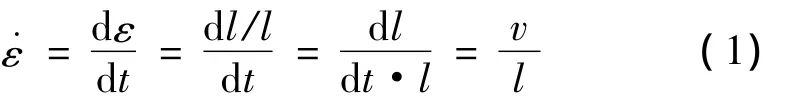
式中:l为试样长度;ν为加载速度。

当加载速度v=5 mm/min时

当加载速度v=10 mm/min时

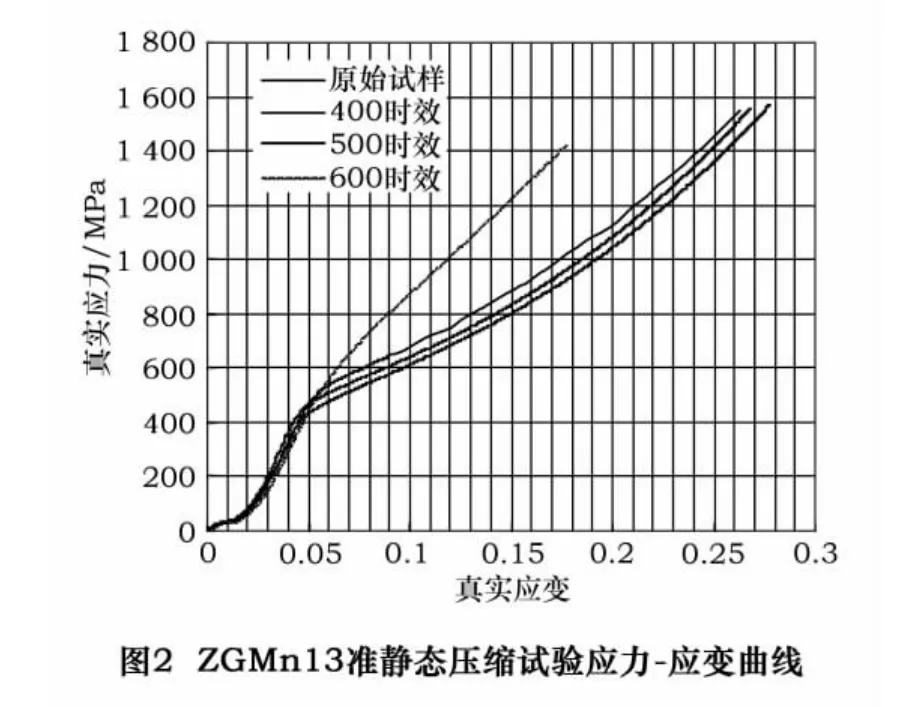
4种时效下ZGMn13高锰钢的准静态压缩应力－应变曲线见图2。

2．2 Hopkinson压杆试验的数据

分离式霍普金森压杆实验（SHPB）已经成为测试材料在高应变率（102～104s－1）下动态力学性能的重要手段之一。高锰钢材料的SHPB试验要满足一维应力假设（只存在轴向应力）、弹性假设（输入杆和输出杆只发生弹性变形）和均匀性假设才能得到有效的测试结果。

根据试验原理［4］，试样中的平均应力 σs、平均应变 εs、平均应变率 εs分别为［4］

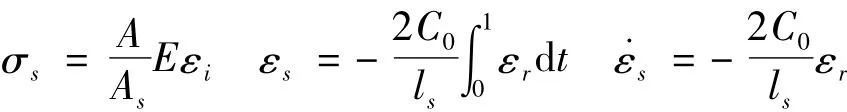
式中:C0为输入杆和输出杆的弹性纵波波速;E为输入杆和输出杆的弹性模量;A为输入杆和输出杆的横截面面积;As为试样的初始截面积;ls为试样的初始长度;εi、εr、εt分别为试样两端面上入射波、反射波、透射波的应变信号。

本文动态力学试验将进行4组试样的测试。试样形状为圆柱体。为保证得到数据准确，4组试样不作抛光和打磨处理，但在其表面涂上黄油以防止在冲击时摩擦对实验的影响。

SHPB基本力学参数:密度ρ=7 740 kg/m3，压杆弹性模量E=206 GPa，输入杆和输出杆尺寸均为φ50 mm×800 mm。子弹尺寸与气压值在各组有所不同，其原因是根据现有的子弹尺寸和空气动力枪可发射的气压情况，只有二者相匹配才可得到所需要的高应变率值，如:想要达到应变率为4 500 s－1的情况，可选取子弹尺寸为φ12.7 mm×190 mm与动力枪发射气压值0.15 MPa的组合方可达到。具体的试验参数见表1。

3 ZGMn13高锰钢Johnson－Cook本构方程

Johnson－Cook模型是最常用的材料模型之一，它形式简单，非常便于数值计算。

Johnson－Cook本构方程的表达式为

式中:σ为VonMises流动应力;ε为等效塑性应变;˙ε为塑性应变率（˙ε*=˙ε/˙ε0）;T*无量纲化的温度项［T*=（T－Tr）/（Tm－Tr）］。模型中有5个未知参数，其中A为屈服强度;B、n为应变强化参数;C为应变率敏感系数;m为温度软化效应;˙ε0为J－C模型的参考应变速率。

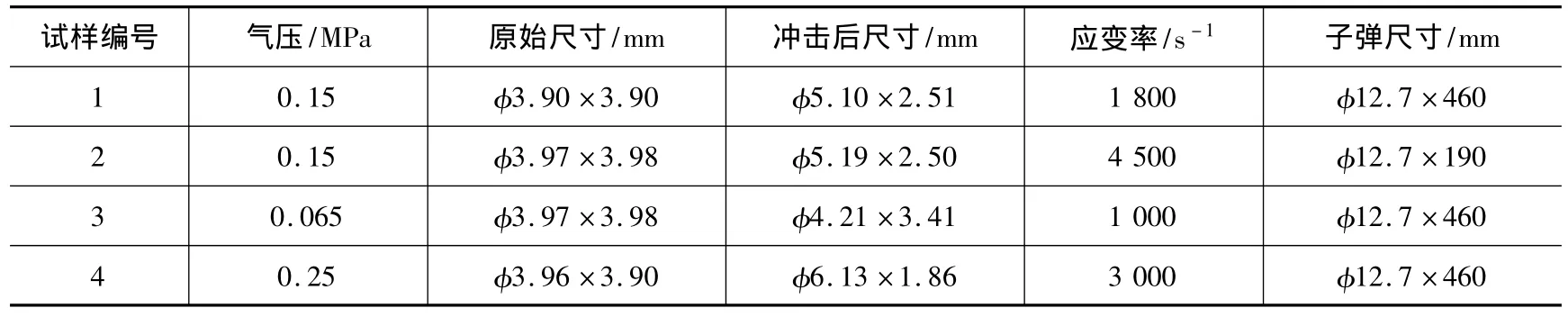
表1 ZGMn13高锰钢的动态力学试验参数

3．1 Johnson－Cook模型中参数的确定

3.1.1 确定系数A、B和n

在不考虑温度变化（即在室温下）和应变率为参考应变率˙ε0=3.39×10－3s－1时，式（4）变为

式中A值为ε=0（指塑性应变）时材料的屈服应力。将式（5）两端取对数并令ln（σ－A）=y，lnB=x，代入式（5）得

根据最小二乘法原理，˙yi能最佳反应yi的条件是残差的平方和具有最小值，即［4］

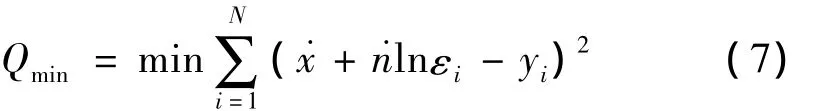
再将Qmin分别对˙x和˙n求偏导并等于零，可解得x、n，从而得出B、n的值。

3．1．2 确定系数C值

不考虑温度变化和在ε=0时，由式（4）可以得到常温下ZGMn13的屈服应力与应变率的关系为

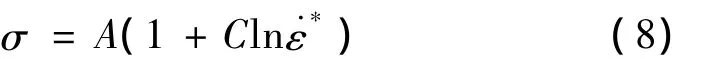
令y=（σ/A）－1代入式（8）得

根据最小二乘法原理，˙yi能最佳地反应yi的条件是残差的平方和具有最小值，即［5］

3．2 ZGMn13高锰钢Johnson－Cook本构方程确立

ZGMn13高锰钢材料在压缩的过程中，屈服点附近没有明显的“平台”现象，使用工程中的条件屈服极限的计算方法，取A=σ0．2，这样就得到了材料的屈服极限 σs=634 MPa，A=634 MPa，B和n由式（7）确定。m取1［6］。由Hopkinson压杆试验所得的数据拟合C，由式（12）确定。最终得到ZGMn13高锰钢的Johnson－Cook本构模型为

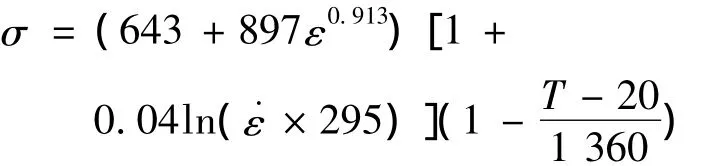
对4种不同热处理高锰钢在常温下的静态和动态力学特性进行测试，由结果可知:虽然高锰钢没有明显的屈服点，但是由试验大致可以看出在相同应变率下，原始试样的屈服极限最高，600时效屈服极限最低，对于塑性阶段而言，原始试样、400时效、500时效应力是依次减小的，但600时效时趋势突然改变，应力变大，超过了原始试样的应力。

4 模型仿真及试验结果

建立斜角切削模型，工件材料用ZGMn13高锰钢，材料本身的塑性属性选用前面确定的Johnson－Cook模型，刀具使用YG8材料，失效准则采用的是剪切失效准则，材料参数及加工参数见表2、表3。

表2 材料参数

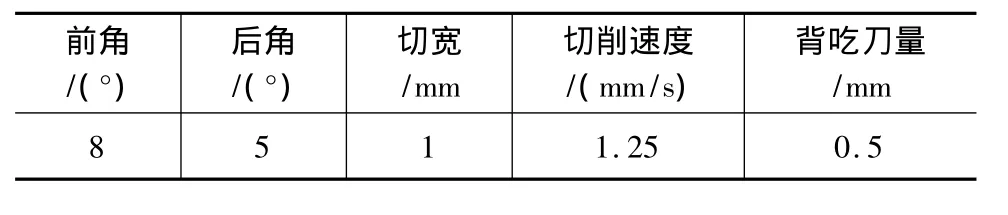
表3 加工参数

切削时的过程为刀具以一定速度切入工件，随着刀具不断地切入，形成连续的切屑，一直到切削力达到稳定状态为止。刀具定义为刚性体，高锰钢定义为弹塑性变形体。采用C3D8RT六面体单元划分网格，刀具和工件的初始温度为20℃。

图3为1.87 s时斜角切削主切削刃上的应力分布图，图4、图5分别为仿真时和试验时主切削力随时间变化曲线。将图4、5两幅曲线进行对比分析如下:

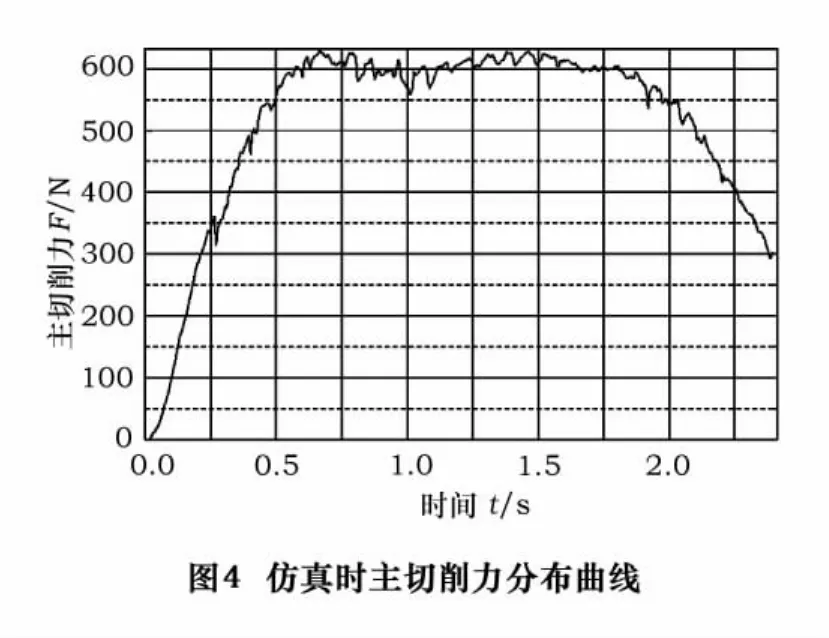
（1）在0～0.5 s阶段，两图切削力与时间呈线性关系上升，说明此时材料正处于弹性变形期，切削力正稳步地增大。

（2）在0.5～2 s阶段，两图材料处于塑性变形期，工件软化切削力略有减小，但都围绕着某一固定值出现了上下波动的现象。仿真时围绕着的固定值大约为600 N，试验时围绕着的固定值大约为550 N。两者的误差为9%。

（3）大约2 s以后，切削力开始减小。

仿真与实验产生的误差及现象的主要原因是:

（1）仿真建模时对刀具作了许多的简化。（例如略去了刀具圆角等）。

（2）在切削力稳定时出现了上下波动，其原因是刀具切入工件后，切削层达到了剪切失效时的应变，工件材料开始破坏，切屑与工件脱离，切削力减小，而后新的材料与刀具接触，切削力又增大，反复进行。

（3）网格划分得不够细，只有足够细小的网格才能准确表达工件、切屑之间的各个物理量。

（4）仿真时工件视为均质材料，但实际加工的工件材料材质不是均匀的。

（5）建立ZGMn13材料的本构模型时，没有考虑温度对材料应力、应变的影响，将温度热软系数m定义为1，在切削过程中，温度对应力的影响也是很大的。

5 结语

本文所确定ZGMn13高锰钢Johnson－Cook本构模型能准确描述该材料的塑性行为，这对于提高高锰钢切削仿真结果具有一定的指导意义。随着今后仿真模型结构的更加细化，切削仿真能更加靠近实际加工。

［1］Hao Xiangyang，Gain Guosheng，Lu Fangyun，et al.Dynamic mechanical properties of whisker PA66 composites at high strain rates［J］.Polymer，2005，46:3528 －3534.

［2］Belyaev S，Petrov A，Razov A，et al.Mechanical properties of titanium nickelide at high strain rate loading［J］.Materials Science and Engineering A，2004，378:122 －124.

［3］Li Qiang，Xu Y B，Bassim M N.Dynamic mechanical behavior of pure titanium［J］.Journal of Materials Processing Technology，2004，155 －156:1889－1892.

［4］刘盼萍，尹燕，等.正火态50SiMnVB钢Johnson－Cook本构方程的建立［J］.兵器材料科学与工程，2009，32（1）:45 －49.

［5］张晓晴，姚小虎，杨桂通，等.用于高强度材料的SHPB实验添加垫块法［J］.实验力学，2005，20（2）:275 －280.

［6］Johnson G R，Hoegfeldt J M，Lindholm U S，et al.Response of various metals to large torsional strains over a large range of strain rates［J］.J.Eng.Mater.Technol.，1983，105:42 －47.