仿OOOE动态分配模型在病床安排中的应用

徐 贤 陈晓明 王俊杰 杨 钱 覃太贵

（1.三峡大学理学院,湖北 宜昌 443002；2.湖北省宜昌市第一中学,湖北 宜昌 443000）

随着医疗服务水平的提高及医院病床资源有限,病床利用的最优化问题得到了广泛的关注.由于医院当前对全体非急症病人采取FCFS（First come,First serve）规则安排住院,导致住院病人等待队列日益变长,为改善此情况医院希望改变FCFS规则以减小排队规模.然而,医院其社会作用的特殊性,使得在进行住院安排时不能仅仅从医院的经济效益考虑,同时需要考虑其社会效益.故在制定新的入院安排规则时需要从医院的经济效益和社会效益两个方面考虑,从而得到一个合理的住院安排规则.

我们借鉴计算机中CPU设计的乱序执行思想,即OOOE（out-of-order execution）思想[1-3],建立仿OOOE动态分配模型,并利用MAT LAB分别按照仿OOOE动态分配模型和FCFS规则进行仿真模拟,从而得到FCFS模型的排队长度是随时间发散,而仿OOOE模型是随时间收敛,因此仿OOOE模型在解决该类问题中具有FCFS模型无法比拟的优越性.

1 研究对象

选取某眼科医院2008年7月13日至2008年9月11日这段时间里患有不同眼科疾病的病人的情况为研究对象,建立排队系统.

1.1 眼科疾病基本信息汇总

医院一般将眼科疾病分为:急诊,单眼白内障,双眼白内障及其他眼科疾病,为描述方便可以将以上眼病编号为1,2,3,4号眼病.由全部原始数据的530个患者信息汇总得到以上4种眼病的信息见表1.

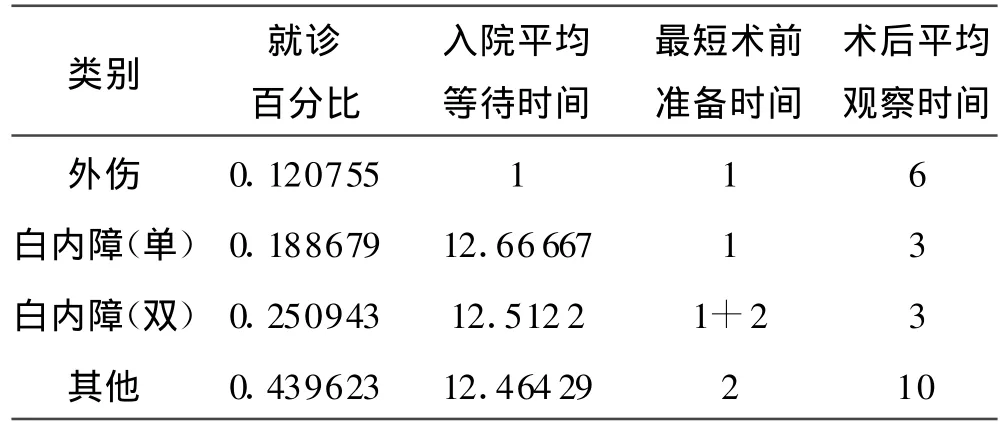
表1 4种眼病的信息 （单位:d）

1.2 术后观察期时间分布

对以上4类眼科疾病同样利用Excel进行统计,各眼科疾病的术后观察的时间所服从分布函数如下:

2 研究方法

2.1 模型评价指标体系

对于病床安排模型,由于其关系到患者与医院双方的利益考虑,故对于一个病床安排模型需要从患者和医院两个方面进行评价.为方便评价,可以取一定时间段T内各项指标值来评价模型.

2.1.1 患者群体评价指标体系

从患者群体利益出发对一个病床安排模型进行评价时,患者群体的需求是:住院等待队列要尽量短,个人等待时间尽量短.因此从患者群体出发对模型的评价可以从以上两个方面确立评价体系.即平均队列长度L、平均等待时间、公平度.

2.1.2 医院评价指标体系

从医院方面出发对一个病床安排模型进行评价时,考虑到病床一直处于供不应求的情况,且容易得知手术收益大于住院收益,因此提高日平均出院人数以及增大主要致盲眼科疾病白内障治愈人数将给医院带来很好的经济效益,所以医院的需求是:日平均出院人数尽量大,白内障治愈数应尽量大.则从医院方面出发对模型的评价可以从以上两个方面确立评价体系.即日平均出院人数、白内障治愈效率.

2.2 仿OOOE动态分配模型

在通常情况下,病床的工作效率的高低反映医院的管理效益和经济效益,同时也是卫生行政部门进行医院评审的重要内容.医院希望有较高的病床周转率,尽量减少患者在医院的逗留时间.对于患者群体,则希望医院在单位时间内治愈更多的患者.因此提高医院的工作效率使医院更加高效运作,应优先考虑让逗留时间较短的患者入住.于是我们在非急诊型眼科疾病病床安排模型中将抛弃FCFS原则,而引入仿OOOE原则对病床分配进行安排.

OOOE是指CPU采用了允许将多条指令不按程序规定的顺序分开发送给各相应电路单元处理的技术[4-5].比方说程序某一段有7条指令,此时CPU将根据各单元电路的空闲状态和各指令能否提前执行的具体情况分析后,将能提前执行的指令立即发送给相应电路执行.当然在各单元不按规定顺序执行完指令后还必须由相应电路再将运算结果重新按原来程序指定的指令顺序排列后才能返回程序.这种将各条指令不按顺序拆散后执行的运行方式就叫乱序执行（也有叫错序执行）技术[2].

本文中OOOE原则思想为:通过确诊获取患者需要手术次数在医院逗留时间等信息,通过对确诊患者信息统计,选择最利于提高医院工作效率的患者即逗留时间最短患者适时入住,而对于积留患者则通过调节机制进行适时的处理调节.

2.2.1 仿OOOE原则入住的确定

由OOOE原则的思想知,只有满足其入院后能按最短术前准备时间手术,才允许其入院.否则,继续等待.又由研究对象的特征,可得对于在医院逗留时间较短的白内障患者在无手术时间限制的条件下安排入住存在优先,且白内障的手术仅在周一、三进行.即单眼白内障的患者仅在周日或周二入住,双眼白内障患者仅在周日入住.那么对白内障患者的仿OOOE原则仅在周日,周二存在优先.

表2 4种眼科疾病入住医院情况

续表2 4种眼科疾病入住医院情况

2.2.2 眼科疾病处理基本优先级

由以上分析可得医院与病人群体都要求提高病床周转率η,因此在对非急诊类的眼科疾病病床安排中,应该优先考虑在医院逗留时间较短的眼科疾病.由表1数据可得1～4号眼科疾病优先级由高到低为:1,2,3,4.

为描述方便引入优先级表示符D=[A1,A2,A3,A4],表示A1～A4优先级依次降低.则眼科疾病处理的基本优先级D0=[1,2,3,4].

2.2.3 优先级调节机制

当采用以上优先级方式安排患者住院时,可能会出现优先级较低的眼科疾病一直积压得不到医治的情形,为改善该类情形引入优先级调节因子M,用以调节1～4号眼科疾病的优先级[6].

（1）优先级调节因子Mk可表示为

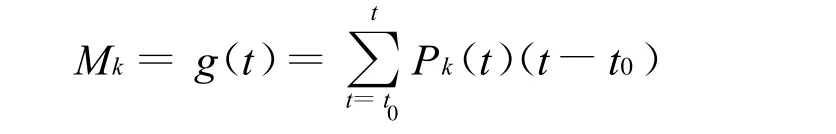
式中,Pk（t）为每天疾病k的确诊总人数,t0为首个积留患者确诊时间,t为检测点.

（2）优先级调节机制

为表示方便引入 f函数,对基本优先级D0进行调节,则调节后的优先级D可表示为

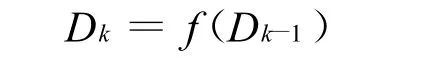
其中,f函数的具体调节机制为

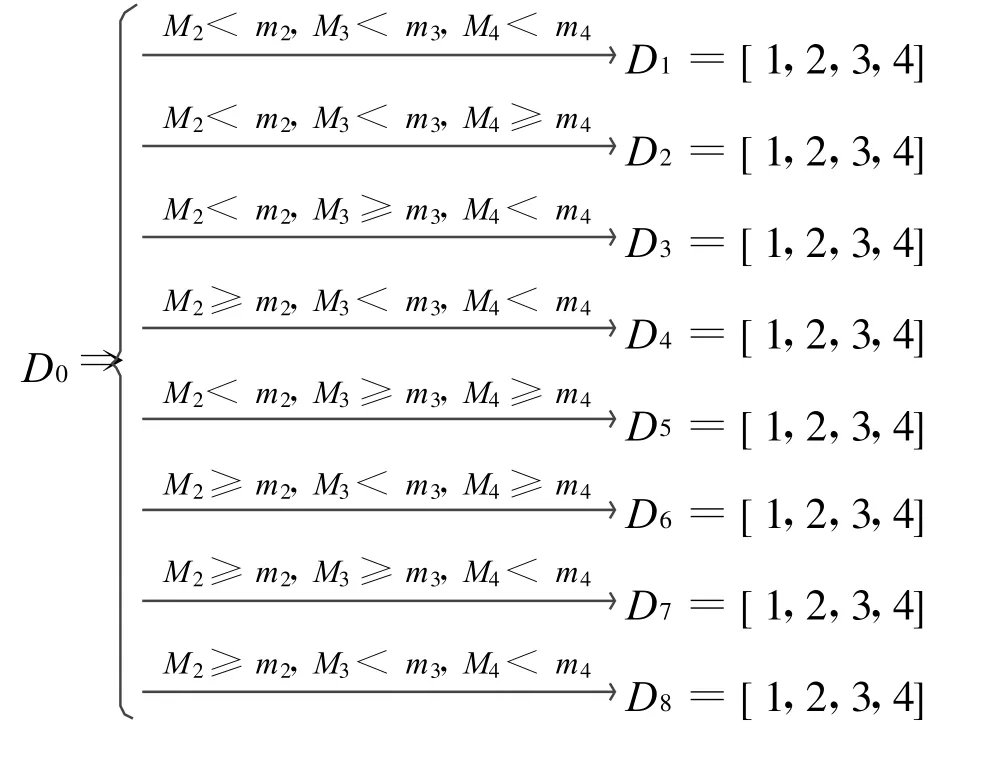
3 数学模型与求解

3.1 目标函数

在目标函数的确立上同样需要考虑患者群体及医院两个方面,故在该多目标问题中可以从各方考虑分别设立目标函数,从患者角度设立平均队列长度L为目标函数,从医院角度设立日平均出院人数N为目标函数,则目标函数有:

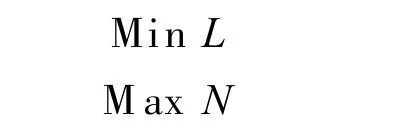
对于以上的两个目标函数,需要求平均队列长度允许最小值,日平均出院人数允许的最大值,且两者的量纲均为人,故可将以上双目标函数转化为单目标函数,目标函数表示为:

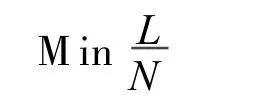
3.2 约束条件

单眼白内障只能在周二、日入住:yij k=0（k=2；j=1,3,4,5,6）.

双眼白内障只能在周日入住:yijk=0（k=3；j=1,2,3,4,5,6）.

同时在进行住院安排时,各眼科疾病患者的住院安排存在优先级问题,且由于人数的积累优先级存在调节.则有约束条件:

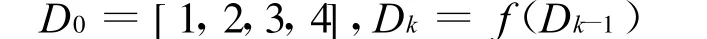
3.3 仿OOOE动态病床数学模型表达

通过以上分析得,数学模型表达如下

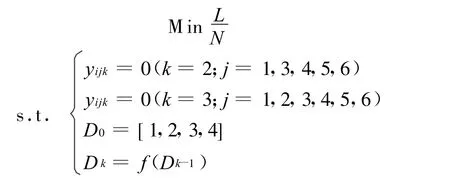
3.4 模型模拟求解

对于以上确立的数学模型,本文采用MAT LAB编程模拟求解,利用计算机模拟流程如图1所示（其中n1为当天出院人数,n2为明天出院人数）.

模拟以9月11号实际在医院的人数为初始条件,按以上仿OOOE动态病床模型进行病床安排,得到9月12号病床安排情况见表3.

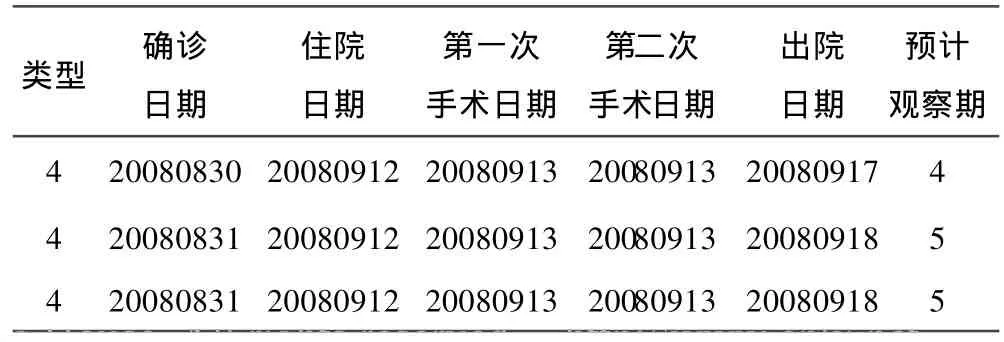
表3 病床安排情况

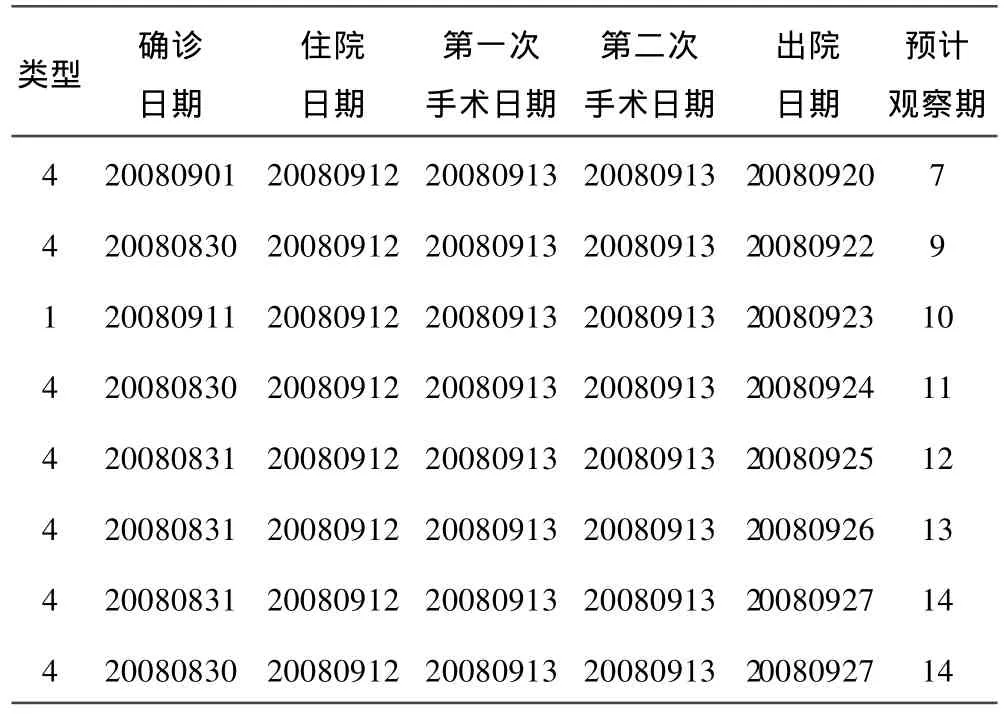
续表3 病床安排情况

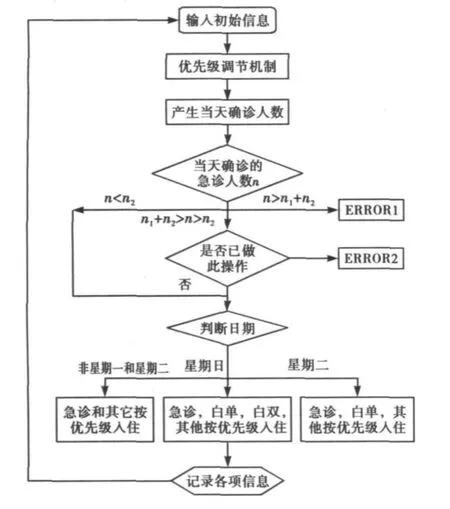
图1 计算机模拟流程

4 仿OOOE模型优度评价

4.1 仿OOOE模型队长与FCFS模型队长对比

为得到仿OOOE动态病床模型及FCFS模型在长期内对医院排队情况的影响,利用计算机进行模拟出同样一批虚拟病人分别运用仿OOOE动态病床模型及FCFS模型的病床安排方案,统计每一天的队列长度.本文中模拟出2008年9月12号以后200d的队长,得到队长变化如图2～3所示.

由图2中可以看出对于仿OOOE动态病床模型的排队长度,随着执行时间的增加,队长在逐渐减小,最终队长稳定在一个较小的范围内,则选取时间段 T=50,得到平均队长L=12.76.而当采用FCFS模型进行病床安排时,由图3得到平均队长L=77.14.

由对比可得仿OOOE动态病床模型在缩短排队队长上比FCFS模型要优.

4.2 仿OOOE模型与FCFS模型平均逗留时间、日平均出院人数、白内障治愈效率、公平度对比

在其他指标的求取中取时间段T=200即整个模拟阶段,同样利用以上模拟所产生的数据统计,有:仿OOOE模型中的平均等待时间=6.4554；FCFS模型中的平均等待时间=8.9747；仿 OOOE模型中医院的日平均出院人数a=9.41；FCFS模型中医院的日平均出院人数a=9.08；仿OOOE模型中的白内障日平均治愈人数c=4.155；FCFS模型中的白内障日平均治愈人数c=3.985.

当仿OOOE模型达到稳定时,平均队列长度L=12.76,各患者队伍的长度均较短,在短时间内都能满足其住院要求.故在该情况下利用公平度指标考察模型意义不大,则不再利用公平度对模型进行评价.

4.3 仿OOOE动态病床模型可预见性与FCFS模型可预见性对比

对于FCFS模型,我们利用同一随机函数模拟产生病人,利用FCFS模型进行病床安排.但经过多次模拟结果发现对于其队列长度是一个随机变化的,难以找到一个稳定的均衡的队列长度.

图4～5为两次模拟运用FCFS模型安排病床队列长度变化值,由两个图形对比不难看出FCFS由于其接诊患者的随机性导致其队列长度难以达到一个稳定均衡的值.

对于仿OOOE模型进行同样的模拟,得到了稳定均衡的队列长度,如图6～7所示.以上两次模拟达到稳定后的平均队列长度基本一致.由上述分析知,FCFS模型的排队长度是随时间发散,而仿OOOE模型是随时间收敛,因此仿OOOE模型在解决该类问题中具有FCFS模型无法比拟的优越性.

5 结 语

对仿OOOE模型与FCFS模型各项评价指标汇总见表4.

表4 仿OOOE模型与FCFS模型评价指标比较

通过对以上表格的数据对比中不难看出,仿OOOE模型在减小患者的排队时间、减小整体的排队人数和提高医院工作效率方面,都要优于FCFS模型.特别值得提出的是仿OOOE模型在减小队列长度上有十分显著效果.即认为仿OOOE模型可以较好得解决实际问题中多群体排队等待服务问题.

[1]王卫国.电脑组装和维护入门与提高:软件入门与提高[M].北京:清华大学出版社,2006.

[2]宁永波,李 谦,李 强,等.一种基于数据相关性的乱序处理器验证方法[J].电脑知识与技术,2011（4）:829-831.

[3]刘李鹂,高智勇,刘向明.基于小波变换的模极大值图像边缘检测算法[J].中南民族大学学报:自然科学版,2006,25（4）:42-45.

[4]仲崇煜,刘大栋,刘月梅.医院实施综合目标管理的经济效益分析[J].中国卫生经济,2001,20（9）:19.

[5]汤志忠,杨春武.开放式实验CPU设计[M].北京:清华大学出版社,2007.

[6]金其林,陈 瑜,王颖丽,等.排队论模型测定社区卫生服务机构编制与人力配置[J].解放军医院管理杂志,2009（2）:59-62.