无线传感网优化生存时间的分布式功率控制*

陈友荣，刘半藤，程菊花，俞 立

(1.浙江树人大学信息科技学院，杭州 310015；2.浙江工业大学信息工程学院，杭州 310032)

无线传感网是由很多具有感知、计算和通信能力的能量有限节点组成。目前，低成本的无线传感网已经应用于很多现有和未来设想的领域，如智能电网、环境监测，战场监视，医疗保健和智能家居等，越来越受到学术界和产业界的关注［1］。

网络生存时间是无线传感网最重要的指标之一，但是研究者没有对网络生存时间进行统一定义。对于一个节点能量耗尽就会影响整个无线传感网的正常应用，网络生存时间可以定义为网络开始运行到网络中第1个节点能量耗尽的这一段时间［2］，也可以定义为网络运行到网络中第1个节点数据不能达到Sink节点时的这一段时间。对于其它一些应用，网络生存时间可以定义为网络开始运行到一部分节点(如半数节点)失效的这一时间段。在无线传感网中，由于节点大多采用电池供电，其能量有限，一旦节点能量耗尽，该节点就会失效，这将影响到网络的运行，甚至导致网络出现分裂而缩短网络生存时间。因此，无线传感网的各个算法都需要从节能出发，最大限度地延长整个网络的生存时间。

为了延长网络的生存时间，无线传感网的很多算法采用各种传输策略(如路由，功率控制和调度等)。其中节点发送功率控制机制是无线传感网的拓扑控制研究方向之一［3］，它主要是调节网络中每个节点的发送功率，在满足网络连通度的前提下，均衡节点的单跳可达邻居数目，剔除节点间不必要的通信链路，形成一个数据转发的优化网络结构，从而达到优化生存时间的目的。

目前，优化生存时间的算法研究已取得一些成果。文献［4－6］分别研究所有节点静止，Sink节点移动时的无线传感网和无线视频传感网的生存时间最大化问题。用分布式的线性规划公式表示路由问题，并采用对偶分解和次梯度方法求解最优路由方案，最大限度提高网络生存时间。但是这些算法都假设已知所有节点的发送功率或通信距离，没有考虑功率控制问题。然而很多无线传感网的应用具有高密集性，在相对拥挤的网络中，众多邻居节点加剧了许多无线网络的特有问题，调整节点的发送功率可以有效的提高网络生存时间。很多学者提出很多功 率 控 制 算 法 如 VRTPC［7］，PCAP［8］，LMA and LMN［9］，CBTC［10］等.文献［11］提出一种新的功率控制算法。该算法采用近邻算法评估网络的密度和计算相应的最优发送功率。每个节点根据最优发送功率发送数据。该算法虽然提高了网络生存时间，但是它是集中式算法而且只适用于节点均匀分布的网络。因此，综合一些学者的观点，结合功率控制和最大化生存时间问题提出无线传感网优化生存时间的分布式功率控制算法(DPCOL，Distributed Power Control for Optimizing Lifetime in Wireless Sensor Networks)。该方法建立生存时间最大化网络模型，通过分布式发送功率迭代和次梯度方法求解该模型，获得当前拓扑结构下的网络生存时间、节点转发概率和发送功率的局部最优值。该算法能有效平衡节点能耗和邻居节点数量，延长网络生存时间。

1 网络模型建立

在算法中，假设:

(1)Sink节点和所有普通节点是静止的，位置固定不变，但是各节点不知道整个网络拓扑结构信息，只通过邻居节点间相互通信获得邻居节点信息；

(2)普通节点具有相同的性能(如初始能量、能耗参数、最大发送功率、最小接收功率等)，而且节点发送功率是可调；

(3)网络统一能量模型；

(4)所有普通节点都需要感知数据，并通过直接或多跳的方式把数据发送给Sink节点；

(5)每个普通节点能量受限，但Sink节点能量不受限制。

以G(V，L)表示一个功率控制的无线传感网，其中，V是由网络节点所组成的非空集合，|V|是网络中节点的数量，L是网络中无线链路(也称为边)的集合。由于每个节点的发送功率不一，存在节点i接收到节点j的数据，但其数据发送不到节点j的情况，因此G是一个有向连通图。如果节点i能发送数据到节点j，则称节点j是节点i的发送邻居节点。如果节点i能接收到节点j的数据，则称节点j是节点i的接收邻居节点。以链路L(i，j)表示节点i到节点j的链路。Nt(i)表示节点i所有发送邻居节点的集合。Nr(i)表示节点i所有接收邻居节点的集合。用网络连接矩阵A表示节点间的关系，其中矩阵A中的元素定义为:

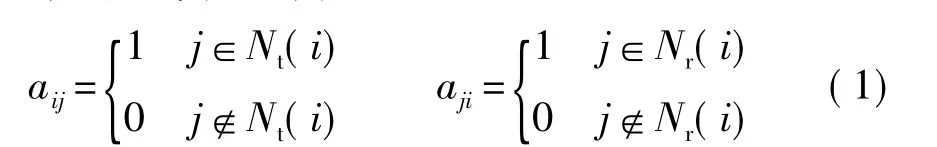
在数据传输过程中，采用Friss自由空间模型计算发送功率和通信距离的关系［12］，公式如下:

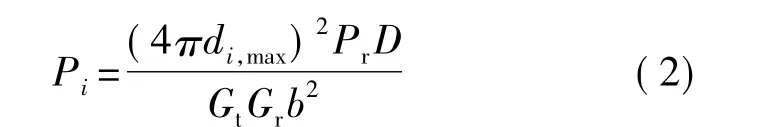
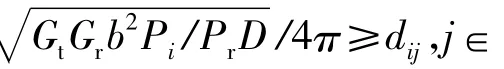
以Fij表示节点i发送给节点j的数据发送速率，以Si表示节点i感知的数据速率，F(i)表示节点i所要发送的总数据速率，则F(i)由Si以及从邻居节点接收到的数据组成，即链路流量平衡等式是:

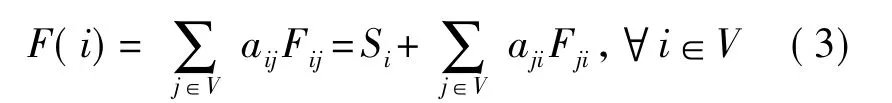
由于节点传输的带宽资源有限，链路上的数据传输速度也是有限，即链路最大传输速率约束是:

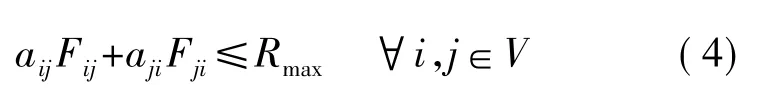
其中，Rmax表示链路的最大传输速率。

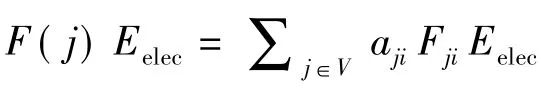
假设节点i的生存时间是Ti，根据定义，网络生存时间则为:

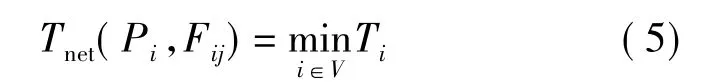
最大化生存时间问题的目标就是求解Pi和Fij，使网络的生存时间最大，即:

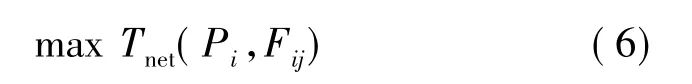
令q=1/Tnet(Pi，Fij)，假设节点i的初始能量是Ei，式(6)可转换成min(q)。因此，功率控制的最优网络生存时间问题可以转换成如下:

2 模型求解

由于约束条件(8)中存在非线性项FijPi，最优模型(7)是一个非线性问题，不能采用次梯度算法。如果发送功率已知，最优模型能通过次梯度算法求解。因此可以结合确定发送功率的遗传算法和次梯度算法求解网络生存时间，但是它是集中式算法，而且涉及到太多变量，计算量大且收敛速度慢。因此采用分布式发送功率迭代和次梯度算法求解。节点随机选择可选集合中的发送功率，并利用次梯度算法分布式求解当前发送功率下的生存时间，完成迭代后获得网络生存时间的局部最优方案。

2.1 已知发送功率的分布式次梯度算法

假设已经确定每个节点的发送功率，节点收集周围邻居节点的信息，并采用分布式次梯度算法求解生存时间最大化模型(7)得到节点生存时间和邻居节点速率［4－6］，其主要算法如下。

根据模型(7)，假设所有节点的生存时间相同，网络生存时间最大化问题可以转换成每个节点生存时间qi的平方和最大化问题。此时如果节点qi值存在最小值，网络生存时间q也存在最小值。即:

对模型中所有自变量(qi和Fij)，式(10)不是凸函数，因此需要引入所有节点数量发送速率Fij的二次正规化项，使得最优化模型是严格凸的，这个优化模型可以定义成:

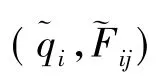
根据上述，可得到如下模型:

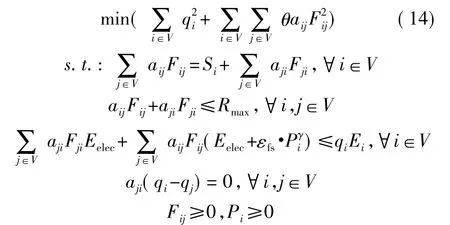
采用次梯度方法求解最优模型(14)，其拉格朗日方程如式(15)

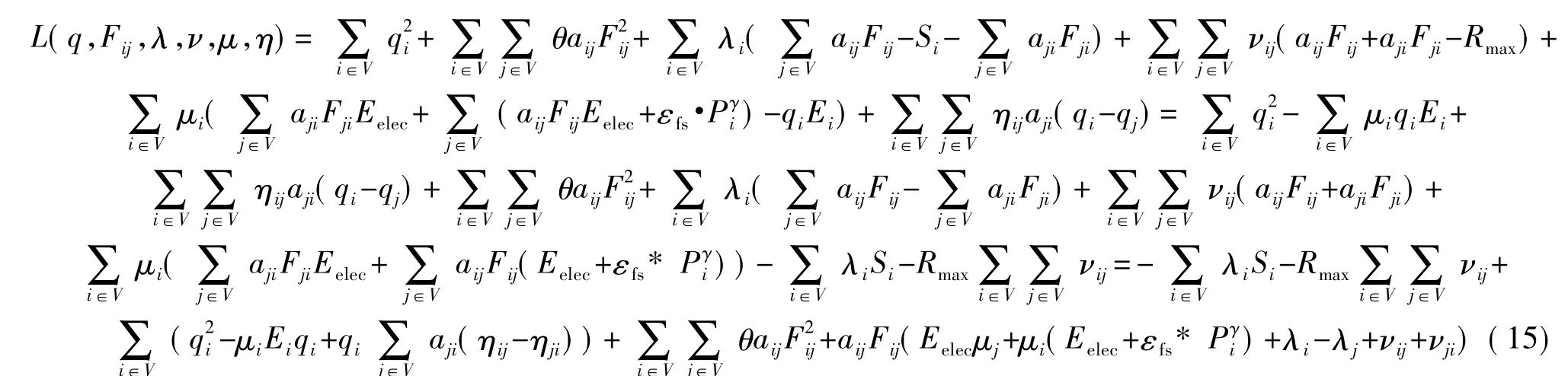
拉格朗日对偶函数G(λ，ν，μ，η)是已知自变量qi，Fij的函数L(qi，Fij，λ，ν，μ，η)最小值，即可以表示为:

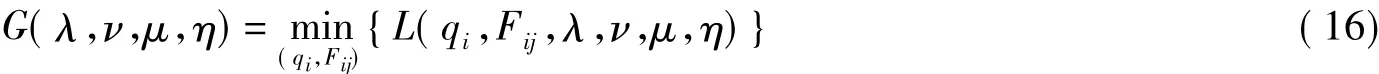
针对式(14)的最优模型，可以转换成拉格朗日对偶问题:

拉格朗日对偶问题的目标函数是凹可微函数，可以使用次梯度方法来解决。

如果在第k次迭代的步长θ(k)(k＞0)满足非可求和递减规律，随着迭代的增加，式(14)的解收敛到最优解。即:

使用次梯度，第k+1的迭代时的对偶变量由以下公式更新:

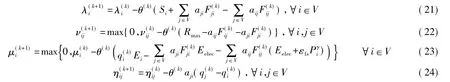
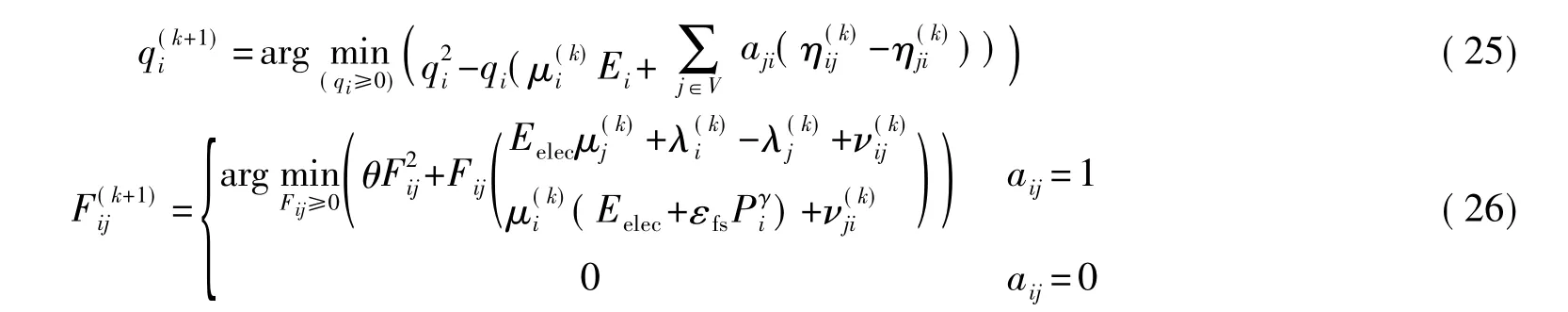
2.2 DPCOL 算法实现

为了指导节点有针对性选择其发送功率，减少选择的复杂性，在DPCOL算法运算前需要确定节点的可选发送功率集合，只选择该集合中的功率作为当前发送功率。集合具体建立方法如下:网络刚开始时，每个发送节点为建立发送功率集合，依次从最低发送功率到最大发送功率递增发送hello数据包。当邻居节点第一次接收到该节点的数据包，则以最大发送功率反馈一个自身信息数据包(包内含有该节点ID信息，hello数据包的ID等)。发送节点接收到邻居数据包后，获知与该邻居节点通信所需要的最小功率，添加到发送功率集合中。

当节点完成发送功率集合的建立后，随机选择集合中的发送功率，利用次梯度算法迭代计算节点迭代过程中的最优生存时间。为了保证网络所有节点都能找到一条到Sink节点的路径，发送功率选择时需保证网络的连通性。在运行次梯度算法时，节点需要邻居节点的相关参数信息(具体包括Fji，λj，μj，ηji，νji，其中j∈Nr(i))，因此节点需不时向其邻居节点发送包含其参数信息的最新预测数据包。邻居节点接收预测数据包后，更新内部相关信息。

网络中节点获知可选发送功率集合P，初始化以下各个参数:节点初始能量Ei，节点感知速率Si，能耗常数Eelec，放大数据信号能耗因子εfs，链路最大传输速率Rmax，Friss自由空间模型中参数Gt，Gr，D，b，Pr，拉格朗日因子(λ，ν，μ，η)0等。完成初始化后，节点执行DPCOL算法计算当前拓扑结构下的网络生存时间局部最优值，每个节点的发送功率和链路的转发概率。其具体的算法实现如下:

步骤1:网络开始时，节点建立可选发送功率集合，并初始化算法中的各个参数；

步骤2:网络节点随机选择发送功率集合中的功率。为保证网络的连通性，节点采用数据包查询的方式，保证选择该功率时，至少有一条到Sink节点的路径，否则重新选择其他的发送功率；

步骤3:确定发送功率后，运行次梯度算法，求解该发送功率下节点的最大生存时间。

步骤4:记录局部最优方案时的节点生存时间，节点发送功率和数据转发概率。当发送功率选择迭代次数大于M，迭代停止，跳到步骤5，否则跳到步骤2，此时重新选择发送功率并初始化相关的参数。

步骤5:结束该算法。此后，节点根据预先设置的协议和计算后的邻居节点转发概率发送数据。

其具体的节点伪代码如下:

算法:优化网络生存时间，得到每个节点的局部最优发送功率。

目标:解决式(10)定义的网络模型，约束条件式(2)～式(5)，式(9)，式(11)～式(12)。

输入:相关常数Ei，Eelec，εfs，Si，Rmax，Gt，Gr，D，b，Pr，节点可选发送集合P，(λ，ν，μ，η)0，发送功率选择迭代次数M，次梯度迭代次数K

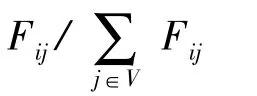
分析DPCOL算法的时间复杂性。如上述伪代码所示，考虑到该算法是分布式算法，每个节点都参与网络生存时间的运算，时间复杂度与网络节点数量无关。其时间复杂度主要有发送功率集合建立和网络生存时间计算两部分组成。前者的时间复杂度由发送功率的递增幅度Δp和节点最大发送功率有关，即Θ(Pmax/Δp)。后者的时间复杂度涉及到M次发送功率的迭代选择和K次次梯度算法的迭代，它的时间复杂度是Θ(MK)。于是总时间复杂度是Θ(Pmax/Δp+MK)。因此DPCOL算法需要一定的迭代时间收敛，而且只有当网络中数据通信所消耗的能量要远远大于最优方案计算所消耗的能量时，DPCOL算法才能较好的工作。

3 仿真实现和分析

3.1 仿真参数

仅考虑无线通信能耗，不考虑路由建立和维护时能耗、分组出错、超时重发所消耗的能量，也不考虑数据计算等能耗。如仿真试验参数表1所示，在仿真试验过程中，选择500 m×500 m网络仿真区域，在该区域中随机分布无线传感节点，计算DPCOL算法下的网络生存时间，并与固定发送功率的次梯度算法比较。

表1 仿真试验参数

3.2 仿真结果和分析

在DPCOL算法中，首先研究分布式次梯度算法的收敛性问题。在仿真区域内随机分布30个节点，所有节点均采用固定发送功率0.37 W/bit，运行次梯度算法获得最优网络生存时间。图1是网络生存时间和其中3个节点生存时间的比较图。如图1所示，在次梯度算法中无论节点生存时间初始值如何变化，随着迭代次数的增加都能收敛到最优网络生存时间。所有节点运行到最后，其生存时间都趋向于网络最优生存时间。因此，分布式次梯度算法是收敛的。

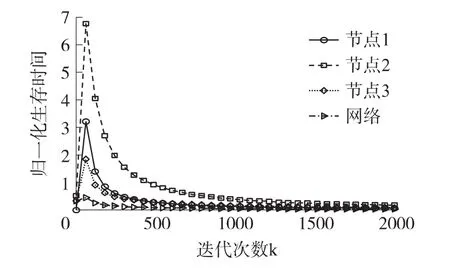
图1 网络和节点生存时间的比较图

图2是200次发送功率选择迭代时30个节点的生存时间曲线图。如图2所示，虚线是每一轮迭代时节点重新选择发送功率情况下的网络生存时间，因为节点发送功率是在可选发送功率集合中随机选择，所以经过次梯度计算的网络生存时间是曲线变化。实线是前m轮迭代过程中生成的最大生存时间。虽然经过M轮迭代生成的最大网络生存时间可能不是整个网络的全局最大值，但是它是局部最优值，在有限的迭代计算中可以明显降低算法的复杂度，提高网络生存时间。

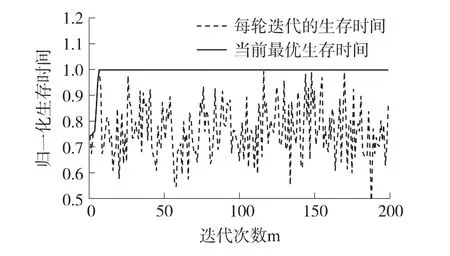
图2 200次发送功率选择迭代的生存时间曲线图

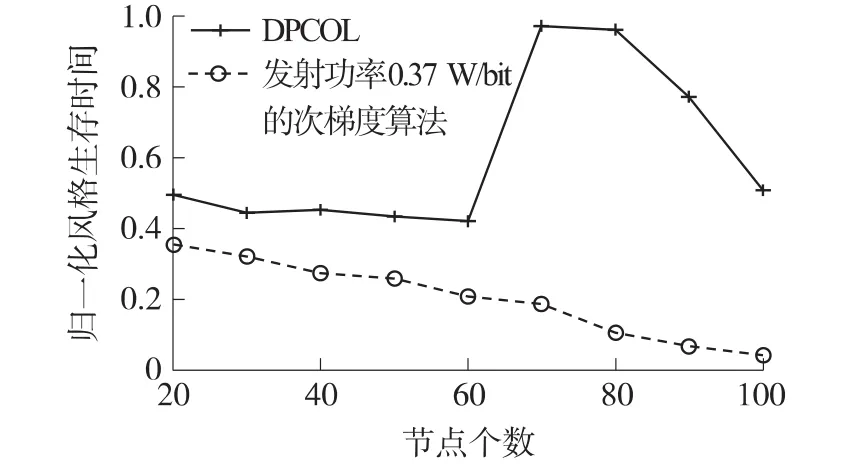
图3 网络生存时间比较图

图3是针对每个给定的节点数，分别比较固定发送功率0.37 W/bit的次梯度算法和DPCOL算法的网络生存时间。如图3所示，选择固定发送功率的次梯度算法时，随着节点数量的增加，因为网络中所有节点都在感知和发送数据，所以节点接收和发送的数据量也随之增加。节点发送功率不变，其能耗也随之增加，网络生存时间减少。但是采用DPCOL算法以后，网络的生存时间比前者明显提高。尤其当节点数量到达70个以后，网络中节点数量多，DPCOL算法选择较小的发送功率，这明显提高了整个网络的生存时间。之后随着节点数量的增加，网络中节点发送数据量也明显增加，这一定程度上提高了网络节点的能耗，降低了网络生存时间。总之，DPCOL算法能提高网络生存时间。

图4是500 m×500 m区域内DPCOL算法的20个节点转发数据概率图。图中节点间链路的粗细代表路径选择概率值。如图4所示，因为很多节点周围有主要发送邻居节点和1个～2个次要发送邻居节点。多个发送邻居节点选择和对应转发概率的引导，可以有效平衡网络节点能耗，提高网络的生存时间。

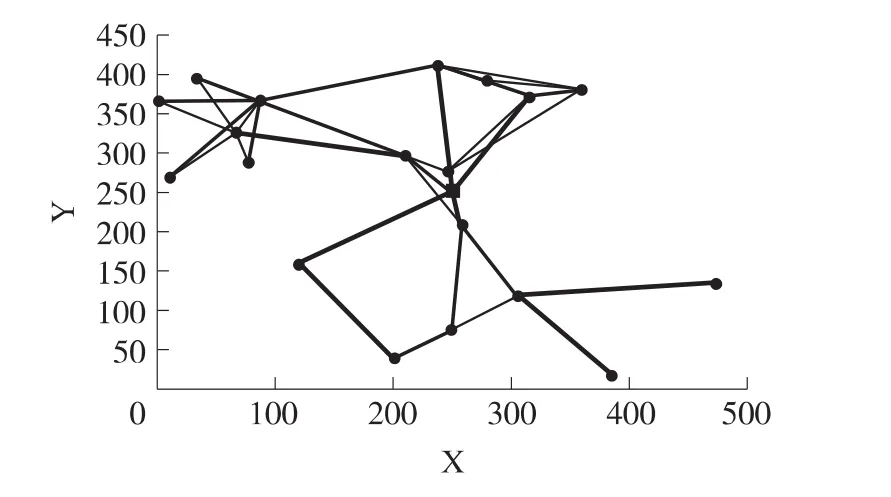
图4 20个节点时的网络拓扑结构图

根据图4的网络拓扑结构图，很多节点周围有多个邻居节点，能选择多个路径发送数据，从而平衡节点能耗。但也不是拥有越多邻居节点越好。分析不同节点数量的DPCOL算法和固定发送功率0.37 W/bit次梯度算法的邻居节点数量。令Ci表示节点i的度值(节点i所有接收邻居节点的数量)。则它的数学期望和方差是:

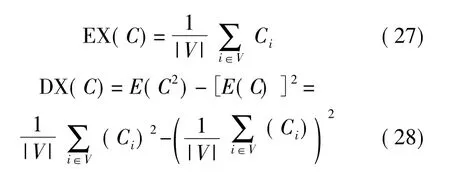
网络度值方差代表网络各节点度值的偏离度。方差小则代表网络节点度值偏差小，每个节点邻居节点数量相差不大。如下图5所示，网络中采用DPCOL算法的度值方差基本上是固定功率的次梯度算法度值方差的1/3。很明显，DPCOL算法选择合适的发送功率，平衡网络节点的邻居节点数量，从而提高网络的生存时间。

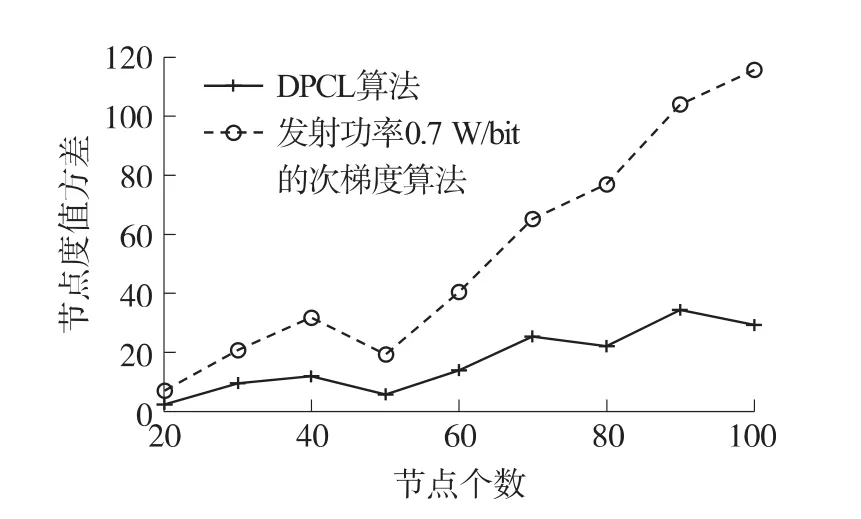
图5 度值方差比较图

4 总结

本文首先建立节点发送功率变化下的网络最大化生存时间模型。其次，采用已知发送功率的次梯度算法求解最大化生存时间模型。接着，提出DPCOL算法的实现。节点随机选择可选集合内的发送功率，并通过次梯度算法分布式计算节点生存时间，即网络生存时间。最后，仿真比较和分析DPCOL算法的收敛性，网络生存时间，拓扑结构和度值方差。

DPCOL算法虽然定义了可选发送功率集合，一定程序上降低了发送功率选择的复杂度。但是还需要迭代选择发送功率和计算此发送功率下的最大化生存时间，所得结果在迭代循环过程中是最优的，但不一定是全局最优值。网络中可能存在其它更优的发送功率方案。因此，接下来的工作是如何分布式选择节点发送功率，从而能得到并证明所计算的网络生存时间是全局最优值。

［1］董齐芬，俞立，陈友荣，等.移动无线传感网中的迭代蒙特卡罗定位算法研究［J］.传感技术学报，2010，23(12):1803－1809.

［2］朱艺华，杨晨曦，吴万登，等.无线传感器网络权衡生存时间与数据分组跳数的分流路由算法［J］.传感技术学报，2009，22(2):273－279.

［3］文凯，郭伟，黄广杰.无线Ad hoc网络中的随机功率控制［J］.电子学报，2008.7，36(7):1304－1308.

［4］Madan R，Lall S.Distributed Algorithms for Maximum Lifetime Routing in Wireless Sensor Network［J］.IEEE Transactions on Wireless Communications，2006，5(8):2185－2193.

［5］Gatzianas M A，Georgiadis L G.A Distributed Algorithm for Maximum Lifetime Routing in Sensor Networks with Mobile Sink［J］.IEEE Transactions on Wireless Communications，2007，7(3):984－994.

［6］He Y F，Lee I，Guan L.Distributed Algorithms for Network Lifetime Maximization in Wireless Visual Sensor Networks［J］.IEEE Transactions on Circuits and System for Video Technology，2009，19(5):704－718.

［7］Gomez J，Campbell A T.Variable-Range Transmission Power Control in Wireless Ad Hoc Networks［J］.IEEE Transactions on Mobile Computing，2007，6(1):87－99.

［8］文凯，郭伟，黄广杰.无线Ad hoc网络中基于节点位置的功率控制算法［J］.电子与信息学报，2009，31(1):201－205.

［9］Kubisch M，Karl H，Wolisz A，et al.Distributed Algorithms for Transmission Power Control in Wireless Sensor Networks［C］//Proceedings of IEEE Wireless Communications and Networking Conference.New Orleans:IEEE，2003:132－137.

［10］Li L，Halpern J Y，Bahl P，et al.A Cone-Based Distributed Topology Control Algorithm for Wireless Multi-Hop Networks［J］.IEEE/ACM Transactions on Networking，2005，13(2005):147－159.

［11］陈友荣，俞立，董齐芬，等.基于近邻算法的无线传感器网络功率控制［J］.浙江大学学报(工学版)，2010，44(7):1321－1326.

［12］WendiB H.Application-Specific ProtocolArchitectures for Wireless Networks［D］.Boston:Massachusetts Institute of Technology，2000.