MAPGIS软件在工程量测算中的应用与探讨

贵州省地质矿产勘查开发局101地质大队 钟 达

MAPGIS软件在工程量测算中的应用与探讨

贵州省地质矿产勘查开发局101地质大队 钟 达

工程建设中需要测算工程量的项目很多，从勘察设计到施工期间由于地质、施工 、设计变更等原因，施工区内的地形地貌变化很频繁，因此，不仅在勘察设计阶段要测量工程量，在施工前、施工过程中、竣工等阶段为控制工程进度、预算分项目经费、最后结算等都需要多次测算工程量。比较常见的几种计算土方工程量的方法有断面法、三角网法（TIN）、方格网法（GRD）、等高线法等。在此介绍MAPGIS空间分析模块提供的两种计算法：不规则三角网法、规则方格网法。

一、不规则三角网法（TIN）

不规则三角网是数字地面模型DTM表现形式之一，该法利用实测地形碎部点、特征点构造三角网，对计算区域按三棱柱法计算土石方工程量。基于不规则三角网建模是直接利用野外实测的地形特征点(离散点)构造出邻接的三角形，组成不规则三角网结构。相对于规则格网，不规则三角网具有以下优点：由于三角网中的点和线的分布密度和结构完全可以与地表的特征相协调，因此可以直接利用原始资料作为网格结点；不改变原始数据和精度；能够插入地性线以保存原有关键的地形特征，以及能很好地适应复杂、不规则地形，从而将地表的特征表现得淋漓尽致。因此在利用TIN计算土方量时其成果精度较其他方法高。其缺点是对不规则的竣工面进行计算时过程复杂，有时甚至不能够进行。

二、规则方格网法（GRD）

对于大面积的土石方估算以及一些地形起伏较小、坡度变化平缓的场地适宜用方格网法。即将场地划分成若干个正方形格网，每个格网结点的高程利用该结点附近高程点通过一定算法求得，然后计算每个四棱柱的体积，从而将所有四棱柱的体积汇总得到总的土方量。MAPGIS规则方格网法是以原始实测地形碎部点、特征点构造方格网GRD1，以竣工后的实测地形碎部点、特征点构造方格网GRD2，再对竣工前后两个方格网进行数学运算得到方格网GRD3（GRD3=GRD1-GRD2），然后对方格网GRD3进行各个区域的填挖方计算（注：此时计算标高均为0）。MAPGIS软件中规则方格网（GRD）模型的建立有四种方法：距离幂函数反比加权法、Kring泛克立格法、稠密数据中值选取法、稠密数据高斯距离权法，选择不同的方法其计算成果精度不一样，下面以一实例进行分析。

三、工程应用

工程项目位于贵州省黔东南地区，属山地Ⅲ类地形，地形较复杂（图1），设计台段复杂，存在不规则曲面，要求计算挖方量与填方量以确定各台段标高使得挖、填方量基本持平。每调整一次标高，就得对整个工程量进行计算，显然在此用不规则三角网法（TIN）进行计算，工作量很大，因此我们采用规则方格网法（GRD）进行计算。为了选择精度较高的方格网计算方法，我们建立了不规则三角网高程模型（TIN）和四种建模方式下的规则方格网高程模型（GRD），以一个水平开挖面分别计算工程量并进行比较，计算范围为整个图形范围（37 500m2），计算面为水平面，标高为928.0m，计算网格间距为2.0m，计算结果见表1。

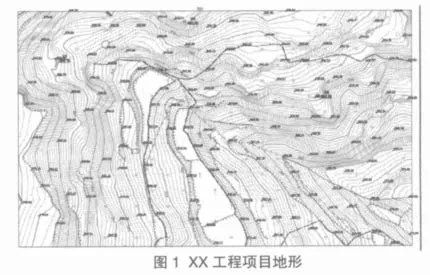
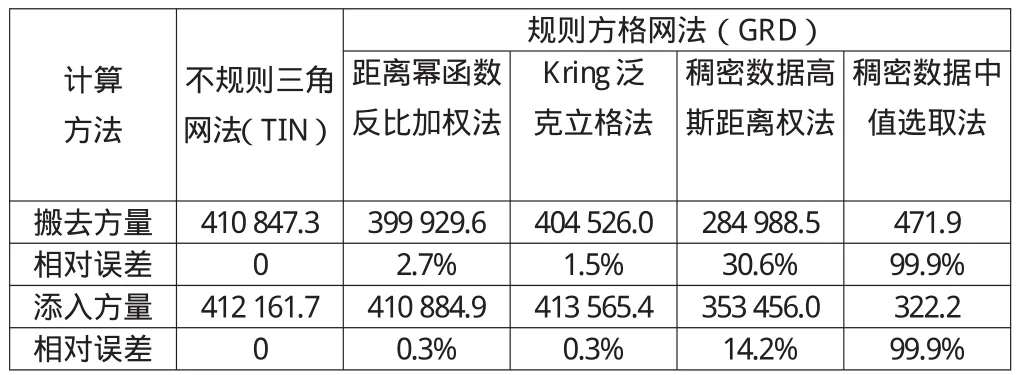
表1 各种方法计算工程量成果对照

不规则三角网法是被普遍认为精度较高的计算方法，在此以其计算结果作为基准进行比较。分析表1数据可以得出：稠密数据高斯距离权法、稠密数据中值选取法构建的高程模型计算结果完全不能满足工程需要，距离幂函数反比加权法、Kring泛克立格法构建的高程模型计算结果能满足工程需要，Kring泛克立格法计算结果更接近不规则三角网法计算结果。因此我们选择Kring泛克立格法作为这个项目的工程量计算方法。实践证明按Kring泛克立格规则网高程模型确定的方案，扣除松散系数的误差，竣工填、挖方量基本持平。

四、结论与建议

通过对以上几种土方量计算方法的比较分析，我们可以得到以下几点结论：一般情况下计算工程量尽量采用不规则三角网（TIN）的计算方法；在采用规则方格网（GRD）计算工程量时，最好采用Kring泛克立格法。总之，在对土石方工程量进行计算时，要考虑到地形特征、精度要求以及计算成本等方面的情况，选择合适的计算方法，达到测算精确的目的。