数学物理方法中MATLAB的应用
谭少轩 李平舟
(西安电子科技大学理学院,陕西 西安 710071)
数学物理方法中MATLAB的应用
谭少轩 李平舟
(西安电子科技大学理学院,陕西 西安 710071)
数学物理方法广泛应用于物理教育、通信、光纤传输等各个领域。其计算复杂,知识内容跨度颇大。使得学生学习物理方法时较为吃力。而 MATLAB作为目前较为流行的数学软件之一,对数学物理方法中图像的处理、复杂公式的计算有相当大的作用。文章就MATLAB处理数学物理方法中的一些函数作出了简单的介绍。
数学物理方法;复变函数;积分变换;特殊函数
(一)引言
数学物理方法是许多理工专业的必修课和重要基础课,是学生进行“电磁场理论”、“光纤通信”以及“微波技术”学习的重要前导课程,也是科研人员常用的基本方法。但它是一门公认的难度大的课程。因课程内容抽象,数学推导繁琐,学生学习起来感到非常枯燥。MATLAB是高性能的数值计算型数学类科技应用软件。具有优秀的数值计算功能和强大的数据可视化能力。在“数学物理方法”中应用MATLAB进行习题求解和计算机仿真,一方面可以提高解题的速度,另一方面可将抽象的解和一些特殊函数以图形形式显示出来.直观明了,物理意义明确。
(二)MATLAB在复变函数中的应用
1.复数计算
例1:求(1 + i )6的实部、虚部、共轭复数、模与辐角。
定义复数后,利用简单的MATLAB语句:real()、imag()、conj()、abs()、angle()可直接得出复数的的实部、虚部、共轭复数、模与辐角。
解:>>a=[(1+i)^6;
>> a=(1+i)^6;
>> real(a)
ans =
0
>> imag(a)
ans =
-8
>> conj(a)
ans =
0 + 8.0000i
>> abs(a)
ans =
8
>> angle(a)
ans =
-1.5708
例2:求方程 027z3=+ 的所有根。
调用内部函数Solve进行求解。
解:>> solve('z^3+27=0')
ans =
-3
3/2 - (3*3^(1/2)*i)/2
3/2 + (3*3^(1/2)*i)/2
2.Taylor级数展开
Taylor级数的展开可以用符号工具箱中的Taylor( )函数直接导出。
解:>> syms z;
>> taylor((z+1)/(1-z))
ans =
2*z^5 + 2*z^4 + 2*z^3 + 2*z^2 + 2*z + 1
3.留数计算
通过求极限的方法计算留数。
解:通过对函数的分析,可知z=0是三阶极点,z=2i,-2i是单极点。
>> syms z;
>> f=(z+2*i)/(z^5+4*z^3);
>> limit(diff(f*z^3,z,2)/prod(1:2),z,0)
ans =
-i/8
>> limit(f*(z-2i),z,2i)
ans =
i/8
>> limit(f*(z+2i),z,-2i)
ans =
0
计算留数.还可直接调用MATLAB函数库中的Residue函数直接计算,见下题。
4.积分计算
积分计算可以转化为留效计算,先求被积函数的留数,利用留数定理求复变幽数的积分。

解::>>[R,P,K]=residue([1],[1,0,5,0,4])
R= %求被积函数的留数
0+0.0833i
0-0.0833i
0-0.1667i
0+0.1667i
P= %四个极点
O+2.0000i
0-2.0000i
0+1.0000i
0-1.0000i K
= %(展开式中无此解析项)

利用MATlAB进行复数运算、级数展开、计算留数、计算积分,操作简单,运算速度快,比起手T计算省时、方便。
5.复变函数的作图
MATLAB可以进行复数运算,也可以进行复变函数的绘图。对于多值函数MATLAB仅对主值进行运算。 MATLAB中表现复变函数的方法是用三个空间坐标再加上颜色的方法来实现。从图形中就可以很容易看出复变函数的某些性质。具体作图时,以XOY表示自变量所在的复平面,以Z轴表示复变函数的实部。而用颜色来表示复变函数的虚部。为了能明确的表示颜色与数值之间的对应关系,通常使用指令colorbar来标注各个颜色所代表的数值。
MATLAB常用的画复变函数图形的指令有如下几种:CPLXGRID、CPLXMAP、CPLXROOT,CPLXROOT(n,m)等。另外,在MATLAB里面,专门提供了复变函数绘图的演示程序、只需在命令行下面输入playshow cplxdemo,即可浏览相应的图形及编程方法,非常方便。
把复变函数理论中经常用到的一些函数做成一个图形界面的绘图程序,通过在下拉菜单中选定函数给定各参数的值,点击即可在相应的坐标平面中得到其图形。由于MATLAB提供了非常方便的图形观察工具,同学们可以通过鼠标的拖曳从空间各个角度观察图形,从而大大加深其对复变函数的理解,掌握它们的一些基本性质。利用这些图形来展示黎曼面,教学效果也非常好。如图求xycossinz=
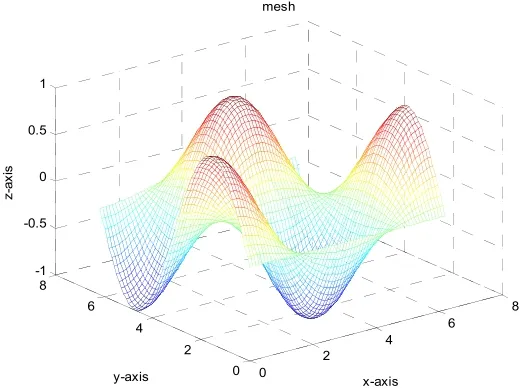
图1 复变函数示意图
(三)特殊函数中的应用
特殊函数始终是“数学物理方法”中的一个重点与难点,大多数学生对此十分头疼。因此,对于特殊函数的教学,除了正常的课堂内容外,我们还采用基于问题的学习方法(Problem Based Learning,PBL)安排了相应的作图实验,要求同学们将教材上所有相关曲线用MATLAB进行绘制,同时作为平时成绩进行考核,并鼓励学生针对学习中的难点自己设计课件,通过作图加深理解。利用这种方法,极大地调动了同学们的学习积极性与主动性,增加了对特殊函数性质的认识。
其编程语言为:x=0:0.01:50 Plot(x,BESSEIJ(15,x))
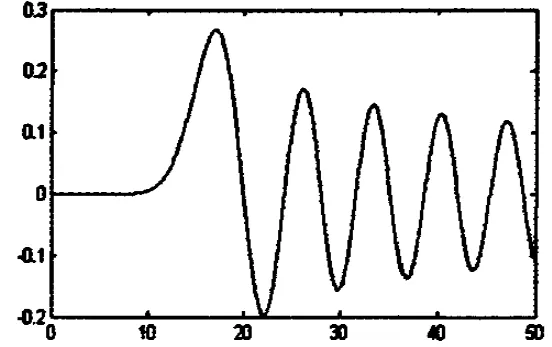
图2 贝塞尔函数15阶 (X)J15 的曲线分布
例2:画出连带勒让德多项式(2阶)的曲线分布。
MATALAB语句为:x=-1:0.01:1;
Plot(x,legendre(2,x))
曲线如图3:

图3 连带勒让德多项式(2阶)的曲线分布
(四)MATLAB在积分变换中的应用
利用MATLAB语句:Fourier(:f.x,w)、laplace(f,x,w),
可将函数f(x)进行傅里叶变换和拉普拉斯变换。而对于积分反变换,则可以用fourier(F)和laplace(L)来实现。编程制作了拉普拉斯变换和傅里叶变换的电子版积分变换对照表,使用该对照表可以进行原函数和变换函数之问的互查。同学们一方面可以对所做题目进行验证,另一方面可以利用该表辅助做题,对于那些无法得到变换函数的题目也可以及早发现,避免无谓的时间浪费。
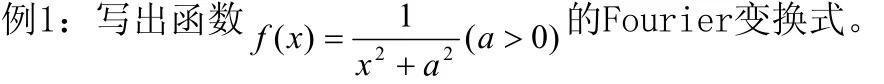
解:>>syms x w:
>>syms a petitive
>>f=1/((x^2+a^2);
>>F=Fourier(f,x,w)
F=pi*(signum(0Re(a)0)*cosh(a*w)-2*Heaviside(w
)*sinh(a*w)+sinh(a*w))/a
例2:已知函数f(x)=x3e−x,试求取该函数的Laplace变换,
并对结果进行Laplace反变换。
解:>>syms x w:
>>f=x^3+exp(-x);
>>F=laplace(f,x,w)
F=6/(w+1)^4
对得出的结果进行Laplace反变换。从而有
>>ilaplace(F)
ans=x^3+exp(-x)
利用手工方法对函数进行Fourier变换和Laplace变换,计算起来繁琐、复杂,且容易出错,利用MATLAB快速、准确。
(五)在解数学物理方程中应用MATLAB
对于大多数的数学物理问题,很难或根本不可能得到其解析形式的解,因此,在教授给学生如分离变量法、格林函数法以及保角变换法等内容的同时,数值方法也是必不可少的环节。在设计的教学实验里,利用MATLAB环境下的PDETOOL工具箱,可以教授同学们掌握以有限元法为代表的数值方法。由于是图形界面,所以同学们上手很快f但需要根据问题的边界、方程的类型设置各种参数,所以学生必须熟练掌握三类边值问题、三种数理方程以及所谓的施图姆一刘维尔本征值问题。当实验内容是结合教材上的例题进行时,同学们会非常惊讶于解析法的繁琐以及数值方法的简便、功能的强大,从而会以更大的热情投入到学习当中去。
例:在矩形域-0.5<x<0.5,-0.5<y<0.5上求解2u−=Δ,且u在边界上的值为零。
利用偏微分方程下具箱求解过程如下:
1.启动偏微分方程求解界面。
2.在MATLAB命令窗口中输人pderect([-0.5 0.5 -0.5 0.5]),选择Boundary Remove All Subdomain Borders菜单项,得出偏微分方程的求解区域。
3.单击偏微分方程界面工具栏中的PDE图标,选择其中的Parabolic选项,将给定的偏微分方程的参数输入到该对话框中。
4.边界条件由Boundary菜单下的Specify Boundary conditions确定,输入边界条件h=l,r=0。
5.单击工具栏等号按钮,得到偏微分的解,单击图形设置按钮,得出图形。
(六)MATALAB在数学物理方法中其它方面的应用
1.泰勒级数展开
复变函数的泰勒级数展开也是“数学物理方法”教学中的一个重要内容。应用MATLAB的符号工具箱也可以进行泰勒展开。比如,使用taylor(f,m,a)函数就可得到f(x)在a点的m阶泰勒级数展开式。另外,MATLAB里面还提供了一个图形化的泰勒级数展开工具——TAYLORTOOL,利用这个工具,同学们可以非常直观地看到函数及其泰勒级数展开之间的关系,也可以动态调整输入函数和参数,非常生动。这种交互性可以大大加深对级数展开的理解。
2.部分分式展开
部分分式展开在复变函数里面也占有非常重要的地位,利用它可以对某些复变函数进行洛朗级数展开,可以利用其来计算留数,也可以利用它来进行拉普拉斯变换的反演等。在MATLAB里面,专门提供了部分分式展开的命令,如[r,p,k]=residue(b,a)、[r,p,k]=residue(b,a)等。通过简单的指令,同学们自己就可以验证题目的正确与否,从而有了学习的成就感,主动性也增加了。
以上简单的介绍了一些数学物理方法中的问题怎样用MATLAB来解决。在不断的学习实践中,我们发现我们应该处理好“数学物理方法”和MATLAB以下方面的一些关系,才能更好的掌握所学的知识。
(七)使用MATLAB解数学物理方法中的体会
1.认识主客体
在教学过程中,应坚持以数学物理为主,MATLAB为辅,千万不能把数学课变成计算机语言课,“体脑倒挂”、主次不分。因此,无论是课堂演示、课外作业还是数学实验,都必须紧密结合教材内容,做到有的放矢。要求教师在课前必须做好充分的准备,每一个实例、每一个程序都要精心设计。另外,学生不能依靠计算机语言来完全替代理论的计算过程。我们需知道MATLAB只是验证理论、计算的一种工具。
2.充分调动学习的热情
由于课程内容困难,绝大多数同学都会对教学内容有恐惧心理。因此,必须利用MATLAB的强大图形处理能力及易用性消除大家的恐惧,增加其学习的动力。每次演示的时候,向同学们展示相关内容的最优美的部分,如动画、三维图像、图像的拖曳、声音背景等,从而吸引广大同学的眼球,提高学习的主观能动性。另外,往届同学所编制的一些样本程序同样可以打破同学们的恐惧心理,提高其自信心。
3.抓住学习的本质
尽管MATLAB语言非常简单,但教授学生掌握还是需要一个过程。因此,必须掌握一个尺度,使用正确的教授方法。我们的经验是采用演示的形式,教会基本操作、基本命令,结合具体的例子进行编程。更重要的是,同学们必须学会使用MATLAB强大的联机帮助功能以及联机演示程序所给出的实例。事实上,MATLAB里面包含众多的工具箱。任何一门课程都无法教会同学们精通所有的内容,只有教授大家熟练掌握了自学的本领,才是学习这门语言的捷径。
4.结合各种方法,提高学习效率。
除了常规的教学方法外,在利用MATLAB辅助教学的过程中,作者也试用了基于问题的学习方法等。比如,在特殊函数绘图以及数值计算方法的实验中,要求广大同学自己学习命令,绘制教材上的曲线,求解书本上的例题或作业;在这个过程中,鼓励同学们发扬团队精神,利用集体智慧解决问题;鼓励“头脑风暴法”等的使用。这些方法的应用,一方面挑战了同学们的智力,一面提升了其合作精神,是学习数学物理方法、学习MATLAB语言的有效途径。
(八)结束语
利用MATLAB软件辅助进行“数学物理方法”的教学,形象、直观,且操作简单、易于掌握。在高校办研究室网上调查中,对于本门课程的教学,各项考核内容均为优秀,客观反映了同学们对这种方法的认可。笔者认为今后的工作还将涉及以下方面的内容:MATLAB在数学物理方程求解方面的应用、MATLAB中有限差分法的应用等。另外,对于数学实验,也需要进一步的扩充,并考虑增加同学们的自行设计并验证数学物理方法实验的内容。
[1] 伍新春,等.高等教育心理学[M].北京:高等教育出版社,1999.
[2] 梁昆淼.数学物理方法(第三版) [M].北京:高等教育出版社,1998.
[3] 彭芳麟.数学物理方程的MATLAB解法与可视化[M].北京:清华大学出版社,2004.
[4] 葛美宝.利用MATLAB促进《复变函数与积分变换》的教学改革[JM].科技信息,2009,(30).
[5] 杨冰.闫循领浅谈Matlab在《复变函数》教学中的应用[J].科技信息,2010,(8).
O411.1
A
1008-1151(2011)06-0136-03
2011-04-20
谭少轩(1986-),男,陕西宝鸡人,西安电子科技大学理学院在读研究生。

