导体尖端周围电势分布的有限差分法研究
伊厚会,吴新华,姚延立
(1.滨州学院 理论物理研究所,山东 滨州 256603;2.滨州学院 物理与电子科学系,山东 滨州 256603)
导体尖端周围电势分布的有限差分法研究
伊厚会1,吴新华2,姚延立2
(1.滨州学院 理论物理研究所,山东 滨州 256603;2.滨州学院 物理与电子科学系,山东 滨州 256603)
有限差分法是对电磁场进行数值求解的重要方法.基于有限差分法的基本原理,计算了导体尖端周围的空间电势分布和局部的电场强度并讨论了它们和尖端角度的关系.本文对于理解电势的概念、尖端放电问题以及电场的具体应用起到很好的帮助.研究对数值计算电磁场的本科教学和编程实现有一定的参考意义.
电场;有限差分法;导体尖端
1 引言
自麦克斯韦方程组提出以来,各种用于计算电磁场问题的解析手段被广泛应用并逐渐形成了许多系统而规范的计算方法,如分离变量法、电像法、复变函数法、格林函数法等[1-3].解析法计算电磁场虽然能求出精确解,但具有很大局限性,求解区域要求规则,对每个问题都需单独进行复杂的计算.而对于实际情况下的电磁场问题,由于结构、边界复杂,要求它的解析解并非易事,而且在绝大多数情况下都是无法求解的,只能用近似的解析计算方法或电场数值计算方法计算,或用电场的实际测量或模拟测量技术测得.
随着计算机技术的发展,各种用于电磁场数值计算的方法也得到了相应的发展[4-6].数值计算方法借鉴了数学中偏微分方程数值解法及力学中的数值分析法,从数值分析角度求解电磁场,以期获得满足工程精度要求的近似解.有限差分法是一种数值解法,它将场域进行网格划分,并用有限差分方程近似地替代偏微分方程,然后引入所研究的特定问题的边界条件求解差分方程,得到电势的数值解,进而求得电场[4-6].
本文基于有限差分法的基本原理,计算了导体尖端周围的空间电势分布和局部的电场强度,并讨论了它们和导体尖端角度的对应关系.研究对于本科教学理解电势的概念、尖端放电问题以及电场的实际应用起到很好的帮助.
2 有限差分法简介
对于给定的边值问题,应用差分法把所研究的区域,离散化为很多网格和节点.对任一节点用差商代替微商,从而把所研究区域的偏微分方程变为各个节点上的差分方程组,则求场的微分方程的解就变为求联立差分方程组解的问题.
差分法求解该静态场问题的过程:首先需从网格划分着手决定离散点的分布方式,这里采用正方形网格的节点配置,从而在每个离散点上可得出相同形式的差分方程,有效地提高解题速度.然后按差分、差商的定义,采用泰勒级数展开法进行差分离散化,推导出相应的差分方程.由二维场拉氏方程的差分形式可得,网格节点(i,j)处的电势满足方程:
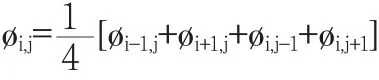
进而可以通过迭代法在误差允许的范围内精确求解电势.根据电势和电场强度的关系E軑=-塄覬,可以计算研究区域任意一点的电场强度.
3 结果和讨论
图1是模拟计算导体尖端处电势分布的二维示意图.研究区域的长度L为500,宽度D为200;计算区域右边界中心处有向内凹陷的尖端,尖端的形状为等腰三角形,深度h=20,角度为θ.研究区域的左边界电势为1,右边界电势为0,其上下边界的电势由左向右依次降低.数值计算的迭代次数为100000时电场稳定,开始分析研究区域的电势分布和局部电场强度.


图2 导体尖端角度θ为30°,60°,90°,120°时的电势分布图

图3 导体尖端顶点A处相对电场强度和角度θ之间的关系
图2是尖端顶角θ为30°,60°,90°,120°时金属导体周围的电势分布图,由图可知,尖端金属导体对电势的影响在其顶尖处和底部更加明显.由于尖端的存在并且尖端的表面是等势面,电势分布随尖端形状做不同程度的弯曲.图3给出了在导体尖端外A点电场强度的大小和尖端角度θ的关系.在计算中定义电场强度的相对量E/E0,其中E0为无尖端时A点的电场强度(即两平行板间的电场强度),E为在尖端顶尖外A点的电场强度.计算结果表明,随着尖端角度的减少,尖端顶尖外A点的电场强度增加.当劈尖角度θ=30°时,A点的电场强度是无尖端时该点的电场强度三倍多.计算结果能很好的解释尖端放电的原因.图4给出了在尖端底端凹陷处B点相对电场强度的大小和角度α的关系,B点相对电场强度的定义和A点相同.计算发现,凹陷处B点的电场强度小于两平行板间的电场强度并且电场强度E/E0随角度α的增加而增大.根据电荷密度和电场强度的关系可知,导体尖端顶尖处的电荷密度远远大于劈尖底部凹陷处的电荷密度.定量的计算结果和理论分析得到的结果相符合[7].

图4 尖端顶点B处相对电场强度和角度α之间的关系
4 结论
本文基于有限差分法的基本原理,计算了尖端周围的空间电势分布和局部的电场强度和劈尖角度的关系.研究对于理解电势的概念、导体表面电荷面密度与曲率半径的关系、尖端放电问题等以及电场的具体应用起到很好的帮助作用,并对数值计算电磁场的本科教学和熟练掌握计算机辅助求解电磁场边值问题提供了参考实例.
〔1〕郭硕鸿.电动力学[M].北京:高等教育出版社,1997.
〔2〕冯慈章.电磁场(第二版)[M].北京:高等教育出版社,1983.
〔3〕Bhag Sing Gurn,Hiziroglu.电磁场与电磁波[M].北京:机械工业出版社,2000.
〔4〕刘圣民.电磁场的数值方法[M].武汉:华中理工大学出版社,1991.
〔5〕胡之光.电机电磁场的分析和计算[M].北京:机械工业出版社,1982.
〔6〕吕英华.计算电磁学的数值方法[M].北京:清华大学出版社,2006.
〔7〕游荣义.锥形导体尖端的电场特性[J].大学物理,2003,22(9):18-20.
O44
A
1673-260X(2011)11-0021-02
滨州学院重点课程(BZXYZDKC200912);滨州学院教学研究项目(BYJYZD201010);滨州学院博士基金(2007Y03)

