时间序列不确定数据流中异常数据检测方法

徐雪松

（南京中医药大学 信息技术学院，江苏 南京 210046）

随着数据采集和处理技术的进步，人们对数据的不确定性认识也逐步深入，许多应用领域产生的不确定数据属于不确定数据流 （uncertain data stream）类型。传统异常数据检测算法[1-3]不适合不确定数据流中异常数据的检测。这些算法只考虑和数据流中确定性成分相结合，并提高异常数据的检测精度，但忽略了不确定数据流高速、无限和动态不确定的特性，使得传统方法无法检测异常数据或需要改进。文中提出一种基于时间序列不确定数据流的异常数据检测方法，该方法充分考虑了数据流的不确定性，同时在计算资源受限情况下自适应地平衡检测计算代价与检测精度。

1 不确定数据流的异常数据检测模型

1.1 不确定数据流的小波分析

文中主要研究时间序列离散类型数据流，其包含的不确定离散元组以数据点概率模型描述。在该模型中，元组的属性值确定，而存在性不确定，用一个[0，1]之间的概率值表示[4]。由于不确定数据流具有非线性及强绕动性，文中采用小波变换来满足自适应时变信号分析的要求，从而可聚焦到信号的任意细节以识别不确定数据流中异常数据。

定义1.1时间序列不确定数据流是一个由相互独立的k维不确定元组构成的序列，S （t）={（w1（t），p1），（w2（t），p2），……，（wn（t），pn）}，其中 wi（t）为 t时刻第 i个元组的值，pi为该元组的存在概率且0≤pi≤1。

其中，a∈R且a≠0；a为尺度因子，表示与频率相关的伸缩，b 为时间平移因子，当时 a=am0，b=nb0a0-m，式（1）为 S（t）的离散小波变换。

设SN（N为分解尺度）表示小波分解中低频信息sN，EN表示小波分解中高频信息 ej（j=1，2，…，N），由于 SN⊕EN=SN-1，即高频信息是低频信息中的正交补，显然多分辨分析的子空间S0可表示为：

令 sN∈SN表示分辨率为 2N的时间函数 S（t）∈L2（R）的无限逼近，ej∈Ej表示逼近的误差，则式（2）可表示为：

由 s（t）=s0，式（3）表明任何时间序列 S（t）∈L2（R）都可根据相应的低频信息和高频信息完全重构。

1.2 异常数据检测模型

小波变换后将包含异常数据的不确定数据流分别分解成包含异常数据的高频信息和低频信息，可采用如下方法识别异常数据。

目前对于确定数据流异常数据在定长时间窗口中的判别可基于欧几里得或者曼哈顿距离度量来决定聚类。基于这样的距离度量的算法对于元组的不确定性十分敏感，这种不确定性通常由概率来表示，参数通常很难确定，特别是对于包含高维对象的数据流来说，这样不仅加重了用户的负担，也使得聚类的质量难以控制。因此，有必要重新定义簇的中心点与半径，使之适应不确定数据模型。

对于不确定数据流的元组，其在定长时间窗口中簇的概率中心Cp定义为簇内元组的概率加权线性均值，Cp=UP1/Ps。

针对定长时间窗口内时间序列不确定数据流，重新定义聚类算法，该定义不但考虑各元组到中心的距离，同时考虑定长时间窗口内元组的平均存在概率对半径值的影响，半径如（4）式所示：

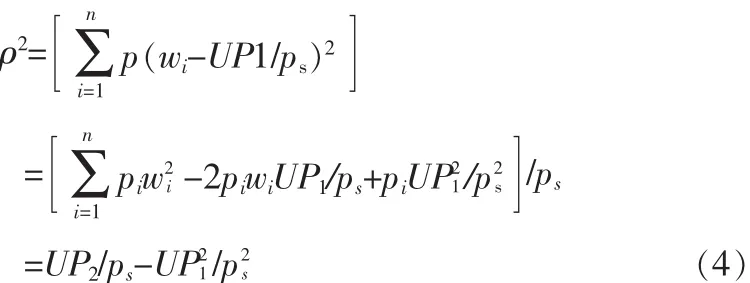
2 算法描述及实验分析

时间序列不确定数据流中异常数据检测算法简述如下：

输入：由时间函数S（t）表示的不确定数据流。

输出：剔除不确定异常数据。具体步骤如下：

1）对S（t）进行小波分解，选定尺度函数、小波函数及其对应的分解系数序列{an}、{bn}和重构系数序列{pn}、{qn}，确定分解尺度N和给出作为判断分解重构达到要求的常数δ。

2）利用小波分解得到N+1组低频、高频信息，分别单独用Mallat塔式算法重构到原尺度上，得到N+1组重构后的时间序列信号。

3）DO

4）从权值给定的时间序列不确定数据流中采样wi（t）//生成样本

5）Cp=UP1/ps//生成簇的概率中心

6）利用4）式计算聚类簇半径

7）if（元组的概率值高于簇的平均概率值，且该元组至中心点距离近）

8）接收该元组为不确定元组

9）else if（元组概率高于簇的平均概率值，且该元组至中心点远）

10）接收该元组为不确定元组

11）else if（元组概率低于簇的平均概率值，且该元组至中心点近）

12）接收该元组为不确定元组

13）else if（元组概率低于簇的平均概率值，且该元组至中心点远）

14）确认该元组为不确定异常数据，应剔除

15）end if

17）if（q（u）/ps≤λ0）

18）该微簇的不确定元组已经陈旧，从内存剔除

19）else接收该微簇

20）end while

以某市中心某路口一个方向的交通流量为例，每个信号周期记录一次（流量单位：辆/周期），2010年8月20日，该路口方向的交通流量曲线如图1所示，该时间序列共测得726个实测数据，文中根据该流量序列，分别运用文中算法和传统的聚类算法对该实测数据集进行异常数据的识别。

文中利用MATLAB小波工具箱的DB4小波函数依据小波分辨分析的原则选定尺度和小波函数，分别得到分解系数序列{an}、{bn}和重构系数序列{pn}、{qn}，为了保证检测精度，确定分解尺度为2。

在该交通流量数据集中共有45个异常数据，直接采用传统聚类算法检测，共检测出了98个异常数据，其中误检了86个，漏检了33个；采用小波分析的不确定聚类算法进行异常检测，共检测到了47个异常数据，其中误检了3个，漏检了1个。表1为这两种算法的检测结果对比。

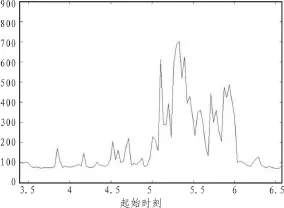
图1 交通流量数据Fig.1 Traffic flow data

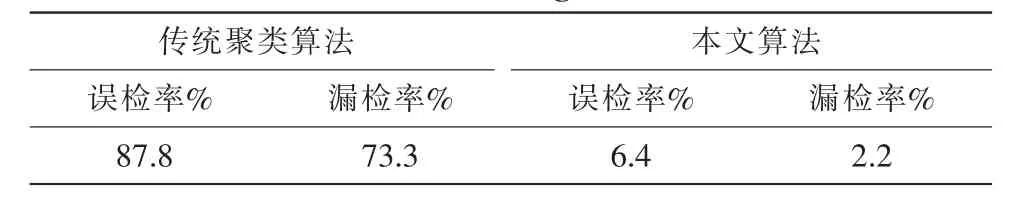
表1 两种算法对异常数据检测结果对比Tab.1 Comparison of the detected results of abnormal data between two algorithms

3 结束语

笔者深入分析时间序列不确定数据流的特点，针对传统数据流异常数据检测方法存在的问题，提出一种时间序列不确定数据流异常数据检测方法。该方法针对不确定数据流的高速、无限和动态不确定特性，结合小波分析和改进的聚类方法来识别异常数据。同时在计算资源受限情况下，能有效平衡计算代价与检测精度问题。实验表明该方法能够较好地满足高速交通流量的不确定数据流异常数据检测的需求。

[1]周春光，邢辉，徐振龙，等.商业数据的预测模型及其算法研究[J].吉林大学学报，2002 ，20（3）:53-60.

ZHOU Chun-guang， XING Hui， XU Zhen-long， et al.Research of prediction models and arithmetic in commerce[J].Journal of Jilin University， 2002， 20（3）:53-60.

[2]JAIN A， CHANG E Y，WANG Yuan-Fang.Adaptive stream resource management using Kalman filters[C]//Proceedings of the 2004 ACM SIGMOD International Conference on Management of Data.Paris， France， USA:ACM Press，2004：11-22.

[3]FALOUTSOS C.Stream and sensor data mining.[C]//Proceedings of the 9th International Conference on Extending Database Technology.Heraklion， Greece， Berlin:Springer-Verlag， LNCS， 2004：25-27.

[4]CORMODE G，McGregor A.Approximation algorithms for clustering uncertain data[J].In ACM Principles of Database Systems （PODS）， 2008：191-200.

[5]彭玉华.小波变换与工程应用 [M].北京：科学出版社，2005.

[6]冯象初，甘小冰，宋国乡.数值泛函与小波理论[M].西安：西安电子科技大学出版社，2003.

[7]王胜坤.JPEG 2000中小波变换的FPGA实现[D].山西：太原理工大学，2007.