中国县域经济差距的收敛性研究
——基于动态面板数据的GMM方法
陈 芳,龙志和
(华南理工大学经济与贸易学院,广东 广州 510006)
中国县域经济差距的收敛性研究
——基于动态面板数据的GMM方法
陈 芳,龙志和
(华南理工大学经济与贸易学院,广东 广州 510006)
基于我国2000—2007年1994个县(及县级市)的非平衡面板数据,采用动态面板分析方法,对我国县域经济发展差距的条件β收敛性进行验证。实证结果表明,我国县域经济存在条件β收敛,通过控制人口增长、产业结构、财政支出和投资力度等方面的地区差异,能有效缩小县域经济间的发展差距。
经济增长;条件β收敛;县域经济;动态面板数据;广义矩估计
1 问题的提出
自20世纪80年代中期以来,经济收敛研究成为经济增长研究领域的热点之一。“经济增长收敛假说”的核心思想源自新古典增长模型(Solow,1956;Swan,1956),该模型认为,资本边际报酬递减规律使落后经济体比发达经济体的增长速度相对较快。因此,经济收敛假说认为,长期来看不同经济体的人均产出水平会收敛于稳定状态。80年代中后期,新增长理论对新古典理论提出了质疑,认为技术进步作为经济增长的核心,可以实现边际报酬不变或递增,即从长期来看各经济体的经济增长并不是趋于收敛,而是趋于发散的。面对新经济增长理论的质疑,新古典增长理论研究者进一步将经济收敛的概念细化为绝对β收敛、条件β收敛、俱乐部收敛、σ收敛等多种类型。其中,条件β收敛假说认为,各经济体的增长速度不仅取决于其期初水平,还受到其资源禀赋、技术进步、投资率、人口增长率,以及地区间要素流动等其他因素的影响。因此,在资本边际报酬递减规律下,具有不同初始人均产出水平的经济体,在长期内不会收敛于同一稳定状态,而是有各自的稳定状态,各经济体的稳定状态由其初始水平以外的其他因素决定[1]。
在实证研究上,自Baumol(1986)关于16个工业化国家经济收敛的开创性研究之后,国内外学者对国家间,或一国内部各地区间的经济收敛问题进行了大量的实证研究,模型不断扩展,分析方法也不断更新。最初普遍采用的研究方法是截面分析方法[2-4],即假定各个经济体具有相同的生产函数,而反映个体差异的变量都被包括在随机误差项里。由于存在遗漏变量、变量自相关、内生性的问题,截面分析方法的估计结果存在偏误。为了解决截面分析中的遗漏变量问题,Islam(1995)将面板分析方法应用于经济收敛研究[5]。为了动态地考察经济收敛特征,学者用经济收敛模型中经济增长水平的一阶滞后项来代替初始经济水平,即用动态面板模型来研究经济收敛,Anderson和Hsiao(1981)提出的一阶差分工具变量法、Arellano和Bond(1991)提出的差分 GMM(广义矩估计法)和系统GMM方法则很好的解决了动态模型中存在的严重内生性问题[6-7]。Anderson-Hsiao的工具变量法是将方程一阶差分,以因变量的二阶滞后或二阶差分变量作为一阶差分因变量的工具变量,保证工具变量的外生性及其与内生变量的相关性。Arellano-Bond的差分GMM方法是用模型中所有变量的二阶及二阶以上滞后值作为工具变量。但是,Blundell和Bond(1998)对差分 GMM 方法提出了批评:当模型中滞后因变量的系数接近1时,即模型接近于随机游走过程时,差分GMM估计会产生弱工具变量问题,而收敛问题中所涉及的宏观变量一般具有时间序列数据持续性,随时间的变动较小,导致原始变量包含的信息不够。于是,Blundell和Bond(1998)提出了系统GMM方法,用一阶差分变量的滞后值作为水平方程的滞后变量,用水平变量的滞后值作为一阶差分方程的工具变量,同时对一阶差分方程和水平方程进行GMM估计[8]。
改革开放以来,我国实行非均衡的经济发展战略,由于经济政策的非均衡导向作用以及地域禀赋的差异性,我国经济发展的地区差异比较明显,如果这种差距过度扩大,不仅会影响整体经济的效率,而且会因收入分配不平等造成的社会问题,影响宏观经济和社会的稳定。因此,实证检验中国区域经济的收敛趋势,把握中国区域经济发展特征,对于缩小地区间经济水平差距,保持中国经济的持续稳定增长具有重要意义。已有大量学者对我国区域经济收敛进行了实证研究,不过现有研究主要集中在省域[9-13]。而关于我国地级以上城市县域经济收敛的研究很少,近年来具有代表性的研究见表1。
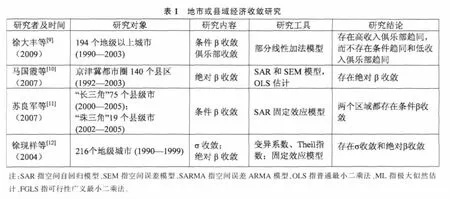
由表1可以看出,一方面,个别涉及县域经济收敛的研究只是针对某些特定地区的部分县区,而少数县区的研究结果并不能很好说明我国县域经济增长收敛的整体情况。在区域经济增长收敛研究中,区域分析单元的选择极为重要,区域单元划分得越细,区域间的不均衡就越接近实际。而且对于我国而言,县是重要的行政单元,县级是国家度量经济发展水平的基本单位。因此,以县为经济收敛研究单元,更能反应经济发展中真实的差异性。另一方面,现有文献一般采用静态分析,不能动态地考察经济收敛特征。
基于此,本文基于我国县域经济面板数据,对我国县域经济的条件β收敛进行动态面板分析。
2 模型简介
新古典经济增长绝对β收敛面板数据模型形式如下:
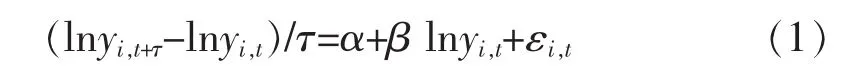
其中,lnyi,t为样本 i在 t时期的实际人均 GDP对数值;(lnyi,t+τ-lnyi,t)/τ为样本 i在时期 τ内的实际人均GDP平均增长速度;α是常数项;扰动项ε~N(0,σ2)。实证研究中,若经济计量结果<0,说明存在绝对β收敛;反之,则不存在绝对β收敛。收敛速度η可根据如下公式进行计算:

同时,根据半衰期公式 e-ητ=1/2,可以计算出落后经济体的人均GDP水平只有发达经济体的一半时,落后城市大致需要弥补该差距的时间T[13]可按如下公式计算:
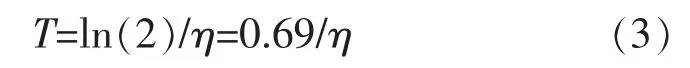
若在模型中加入资本、产业结构、人口增长率等代表研究样本经济结构特征的控制变量,则模型变为条件β收敛面板数据模型:
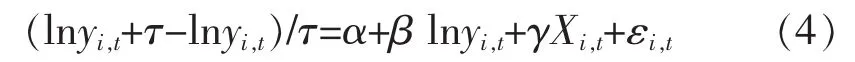
其中,Xi,t为一系列代表t时期样本i经济结构特征的控制变量。参考Bassanini等[14]的动态面板模型,本文用技术进步、劳动力增长率、固定资本存量、产业结构、财政支出和折旧率等变量来描述我国县域经济的结构特征差异,得到动态面板模型如下:
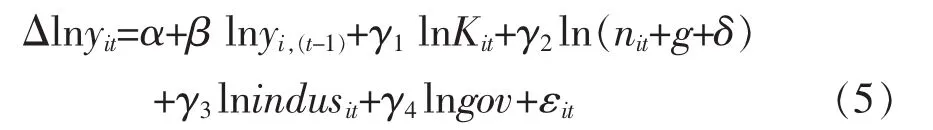
上式也可以写为:
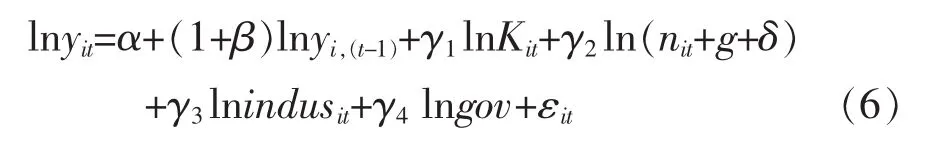
其中 Δlnyit(Δlnyit=lnyi,t-lnyi,t-1)表示实际人均GDP 变动率;yi,(t-1)为上期的实际人均 GDP,为降低模型的内生性,本文中将每期间隔设为两年;β表示收敛系数;K是用永续盘存法估算的人均固定资本存量,n是人口增长率,g为技术进步率,δ为折旧率,indus为产业结构变量,gov为政府投入。
由于动态模型的解释变量中有被解释变量的滞后值,因此该模型存在显著的内生性,这会导致估计结果发生偏差,从而使得根据估计系数无效,需要通过使用工具变量来克服模型中的内生性问题。若经济初始水平lnyi,t的系数β的估计值显著为负,则表明地区间存在条件β收敛,即每个地区都在朝各自的稳态水平趋近,而这个稳态水平跟地区自身的经济结构特征有关,经济体人均产出趋近自身稳态水平的速度称为条件收敛速度,计算公式同式(2)。
3 数据及变量说明
本文用到的主要变量如下:实际人均GDP,代表我国县域经济的经济发展水平,采用居民消费价格指数剔除价格因素;实际人均固定资本存量,作为我国县域经济资本存量的代理变量;产业结构变量,由于县域经济统计年鉴中第三产业增加值的数据缺失值太多,因此本研究用第二产业增加值占第一产业和第二产业增加值之和的比重来反映我国县域经济的产业结构状况;人口增长率,用年末人口增长率来代替;政府投入变量,用地方财政支出占GDP的比重来表示,考察地方财政支出结构对区域经济的影响。
3.1 数据来源
本文中GDP、年末人口、三次产业增加值、全社会固定资产投资总额、地方财政支出等宏观经济变量数据均来自2001—2008年《中国区域社会经济统计年鉴》和《中国县(市)社会经济统计年鉴》;居民消费价格指数来自历年《中国统计年鉴》;固定资产投资价格指数来自历年《中国统计年鉴》。
3.2 数据处理
(1)以2007年行政区划为准,将我国的县和县级市作为初始研究样本,不包括各直辖市的区,样本分布于我国28个省和自治区,仅北京、天津和上海这三个直辖市管辖范围内的县级经济单元没有纳入本文研究中来。
(2)由于2004年进行全国性经济普查,该年数据与其他年份的数据不具有连续性,研究中对其进行平滑处理,即研究中用 2002、2003、2005、2006四年数据的平均值作为该年数据的代替值。
(3)为了消除价格因素对宏观经济变量的影响,采用以2000年为基期的各省居民消费价格指数,对其所辖县的人均GDP变量进行价格调整;采用以2000年为基期的各省固定资产投资价格指数对全社会固定资产投资总额进行价格调整。
(4)由于统计年鉴中没有提供技术进步率和折旧率的有关数据,沿袭多数文献对此问题的处理方法,假定技术进步率和折旧率在研究期内为一常数,且该常数的估计值为0.05。
经过上述处理,得到本文的研究数据为个体N=1994,时间跨度T=8年(2000—2007年)的非平衡面板数据。研究样本1994个县及县级市的空间分布如图1所示。
4 实证分析
通过估计模型(6)对我国县域经济条件β收敛进行实证分析,先后采用普通最小二乘法、广义最小二乘法和系统GMM方法估计模型,以方便比较不同方法下估计结果(见表2和表3)的异同,以下是对每一步估计的具体说明:
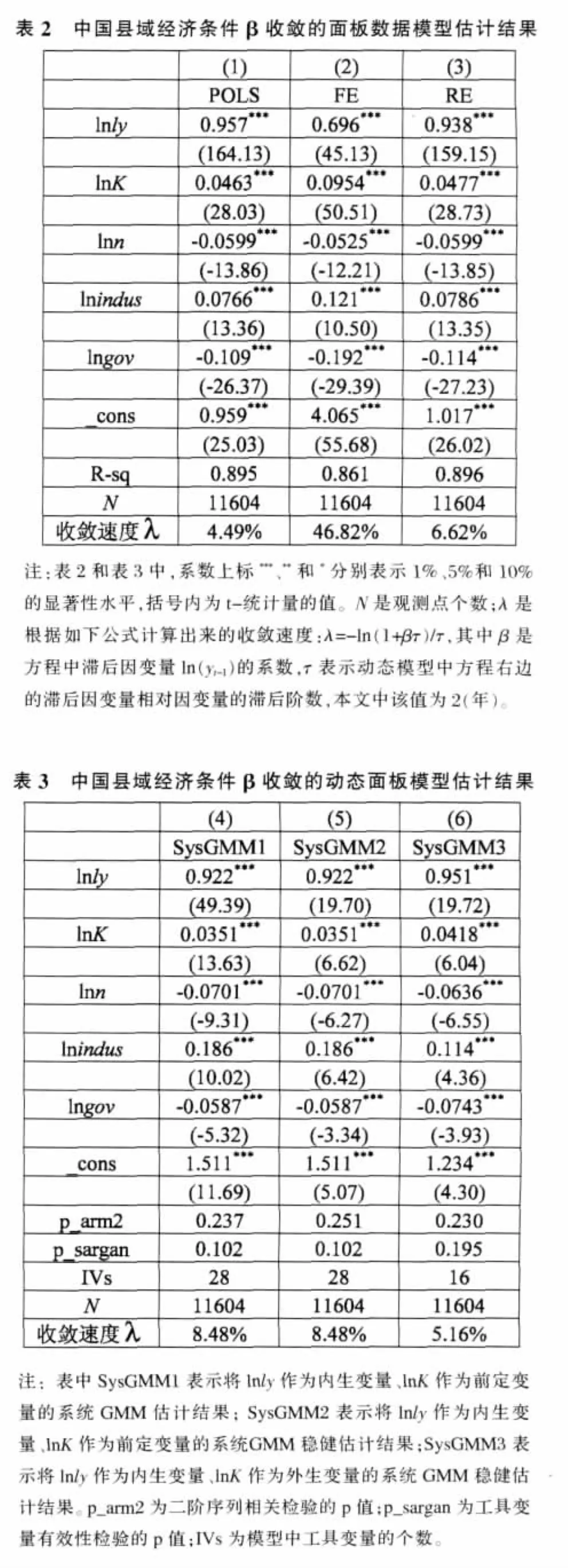
第一步,本文采用普通最小二乘法对混合数据进行估计,结果显示每个变量的系数都很显著,且滞后因变量的系数为负,支持条件β收敛假说,收敛速度约为4.49%,然而,由于模型中存在异方差、自相关、截面相关和严重的内生性,此混合估计结果是有偏的。
第二步,进行Hausman检验以判定采用固定效应模型还是随机效应模型进行面板数据分析,Hausman检验结果拒绝原假设,即选用固定效应模型更合适,本文将固定效应(FE)和随机效应(RE)的估计结果都给出,由表2可以看出,二者结果明显不同,而随机效应(RE)模型的结果更合理。随机效应模型估计结果显示每个变量的系数都很显著,且滞后因变量的系数为负,说明中国县域经济间存在条件β收敛,且收敛速度为6.62%。而Hausman检验下选择的固定效应模型估计的收敛速度为46.82%,显然不合理。这是由于在存在内生性的情况下,随机效应模型得出的结果是有偏误且不一致的,当T越小时,偏差越大,仅当T→∞时,偏差才能消失;同时,固定效应模型估计结果也并非是最有效的,而广义矩估计法(GMM)能较为有效地解决这一问题。
第三步,由于工具变量法能解决内生性问题,却仍无法解决模型中很可能存在的遗漏变量问题。因此,本文用系统GMM方法来解决模型存在的内生性问题。通过检验模型中的工具变量有效性(Sargan检验)和以及二阶序列相关性(AR(2)检验),表3中各结果都不能拒绝Sargan检验和AR(2)检验的原假设,即模型中的工具变量是有效的,且不存在二阶序列相关,由于结果(6)的Sargan检验p值最大,因此,本文选择结果(6)。
由系统GMM估计结果可知,我国县域经济存在条件β收敛,且收敛速度为5.16%。由于条件β收敛的估计是在一系列控制变量的假设下进行的,因此,条件β收敛并不意味着区域经济差异的绝对缩小,而是以某种速度收敛于各区域自己的经济稳态,因此,我国县域经济以5.16%的速度收敛于各自的稳态,这个稳态由模型中控制变量代表的经济结构特征所决定。
另外,从估计结果可以看出,使用不同方法得到的控制变量估计系数比较接近。人口增长率和地方财政支出结构的变量系数都显著为负数,而资本和产业结构的系数显著为正,这表明:第一,地区的实际人均产出与该地区的人口增长率具有负向变动趋势,即从长期来看,人口增长率越高的地区,人均产出越低;第二,地区的实际人均产出与地方财政支出比重具有反向变动趋势,即地方财政支出占GDP的比重越大,则该地区的实际人均产出越低;第三,地区的实际人均产出与该地区的产业升级程度具有正向变动趋势,即产业结构的升级会带来更高的实际人均产出;第四,地区的实际人均产出与固定资本存量有相同的变动趋势,即固定资本存量越高,该地区的实际人均产出越高,且固定资本存量的产出弹性为4.18%。
5 结论
在研究区域差异或经济收敛问题时,区域单元划分得越细,越能反映区域经济的真实差异性,本文采用动态面板分析方法对我国县域经济差距的β收敛问题进行了实证研究,从而较为准确地对我国区域经济收敛特征进行县域层面的认识。
通过对2000—2007年我国县域经济进行动态面板分析。发现我国各县域经济存在条件β收敛趋势,稳健的收敛速度约为5.16%。在研究期内,我国县域经济增长还具有以下几个特征:
第一,人口增长率对人均产出的影响是负向的。这可能是因为我国县域经济存在大量的剩余劳动力,人口增长对县域经济增长的贡献较低,从而导致县域经济总量虽实现增长,但人均产出却出现了下降。由于我国人口增长率高的地区大多为经济落后地区,所以,为了缩小地区间的经济发展差距,应加强县域经济剩余劳动力的转移,有效控制落后地区的人口增长率。
第二,产业结构升级促进我国县域经济人均产出的增长。当前,我国县域经济仍然以农业经济为主,根据本文实证结论,加快产业结构调整,推动县域工业经济加快发展,将有助于提高我国县域经济人均产出水平。
第三,地方财政支出比重的增加未提高我国县域经济产出水平。这一方面可能是因为主要用于基础设施建设的地方财政支出对产出增长的影响存在滞后;另一方面可能是因为地方财政支出的效率较低、支出结构不合理,从而降低了地方财政支出对实际人均产出的促进作用。
第四,固定资本存量的增加对经济增长具有促进作用。增加物质资本投资力度,可以有效拉动县域经济的增长。
综上所述,我国县域经济增长存在条件β收敛,这并不意味着县域经济差异的绝对缩小,而是以某种速度收敛于各区域自己的稳态,该稳态是由人口增长、产业结构、财政支出和投资力度等因素决定的。加强落后地区县域经济剩余劳动力的转移,有效控制落后地区的人口增长率,加快其产业结构调整,推动工业经济加快发展,提高地方财政支出的效率,增加落后地区固定资产的投资力度,能有效缩小我国县域经济的发展差距。
[1]Barro R.,Sala-i-Martin X..Convergence[J].Journal of Political Economy,1992,(100):223-251.
[2]Baumol W..Productivity growth,convergence,and welfare:what the long run data show [J].American Economic Review,1986,(76):1072-1085.
[3]Barro R.,Sala-i-Martin X..Convergence across states and regions [J].Brooking Papers on Economic Activity,1991,(1):107-182.
[4]Mankiw,Gregory N.,David Romer,David Weil.A contribution to the empirics of economic growth [J].Quarterly Journal of Economics,1992,(107):407-437.
[5]Islam N..Growth empirics:a panel data approach[J].Quarterly Journal of Economics,1995,110(4):1127-1170.
[6]T.W.Anderson,C.Hsiao.Estimation of dynamic models with error components[J].Journal of American Statistical Association,1981,(76):598-606.
[7]Arellano M.,Bond S..Some test of specification for dynamic panel data[J].Review of Economic Studies,1991,(58): 277-297.
[8]Blundell R.W.,S.R.Bond.Initial conditions and moment restrictions in dynamic panel data models [J].Journal of Econometrics,1998,(87),115-143.
[9]徐大丰.我国城市的经济增长趋同吗?[J].数量经济技术经济研究,2009,(5):30-41.
[10]马国霞,徐勇,田玉军.京津冀都市圈经济增长收敛机制的空间分析[J].地理研究,2007,26(3):590-598.
[11]苏良军,王芸.中国经济增长空间相关性研究[J].数量经济技术经济研究,2007,(12):26-38.
[12]徐现祥,李郇.中国城市经济增长的趋同分析[J].经济研究,2004,(5):40-48.
[13]Sala-i-Martin X..The classical approach to convergence analysis[J].The Economic Journal,1996,(106):1019-1036.
[14]Bassanini A.,S Scarpetta,P.Hemmings.Economic growth:The role of policies and institutions:panel data.evidence from OECD countries[J].OECD Economics Department Working Papers[C],No.283,2001.
(责任编辑 迟凤玲)
Dynamic Panel GMM Analysis of Economic Growth Convergence in China
Chen Fang,Long Zhihe
(School of Economics and Commerce,South China University of Technology,Guangzhou 510006,China)
In this paper,we use the unbalanced panel data including 1994 counties of China from 2000 to 2007.We construct a dynamic panel model based on the regional economic structure and growth characteristics of China.Then we analyze the conditional beta-convergence across the counties of China with a GMM dynamic panel estimation method.Empirical results turn out the existence of conditional beta-convergence trend among counties of China.Moreover,we also prove that it is helpful to control the regional disparity if the regional differences of population growth,industrial structure,fiscal expenditure and investment gradually reduced.
economic growth,conditional beta-convergence,county economy,dynamic panel data,GMM
F061.5
A
2010-10-25
陈芳(1983-),女,湖南新化人,华南理工大学经济与贸易学院管理科学与工程专业博士研究生;研究方向:区域经济的空间经济计量。

