Harris角点检测算法的优化研究
刘 莹,张久东,周卫红
(云南民族大学数学与计算机科学学院,云南昆明650031)
Harris角点检测算法的优化研究
刘 莹,张久东,周卫红
(云南民族大学数学与计算机科学学院,云南昆明650031)
在研究Harris角点检测算法时,发现检测出的角点常常会受到噪声的影响.通过优化Harris角点响应函数,避免了角点响应函数中k值的影响,提高了每个目标像素点的响应值精度.把该方法运用到人脸特征的检测中,实验结果表明,该算法和传统的Harris角点检测算法相比抗噪能力有较大提高.
特征点检测;人脸识别;噪声;响应函数
特征点检测在图像匹配与配准、目标描述、物体识别等方面得到了广泛的应用,是计算机视觉研究中的热点.现实世界中,人类通过人眼视觉系统来识别物体和不同的人,这个看似简单的过程对计算机来说却非常地困难,计算机要先通过对图像进行数据分析,然后,从中提取出准确、稳定的特征信息来进行识别.所以,特征点的提取直接影响到图像识别的正确率和速率,角点作为特征点的一种,包含了大量的图像信息.目前,特征点提取的算法大概可以分为2种:一种是Kitchen[1]提出的基于轮廓线的方法,另一种就是基于图像灰度值的方法,如Susan法[2]、Harris法[3]等.Harris 检测算法,不受摄像机姿态以及光照的影响,是效果比较好的一种算法,但是它对噪声却比较敏感.
1 Harris检测算法的局限
Harris角点检测算子是 Moravec算子的改进[4-7].Moravec算子是 Moravce 于 1977 年提出的利用灰度方差提取特征点的算子,该算法以目标像素点为中心选取一个二值窗口,计算 0°,45°,90°,135°四个方向的灰度差平方和,取最小值为该像素点的兴趣值.Harris在此基础上提出了用高斯函数代替二值窗口函数,对每一个目标像素点,用Taylor展开去近似任意方向,以此得出兴趣值.假设目标像素点的坐标为(x,y),在x方向上和在y方向上移动的距离分别是u和v,那么,该像素点的灰度变换度量的计算公式如下表示:

写成矩阵形式:

其中,Ex,y为窗口内的灰度变化度量;wx,y为窗口函数,一般定义为 wx,y=e(x2+y2)/σ2;I为图像灰度函数,Ix为 x方向的差分,Iy为y方向的差分,o(u2+v2)是移动距离的无穷小量.矩阵M是目标像素点的自相关矩阵,它的2个特征值分别为λ1和λ2,这2个特征值与矩阵M的主曲率成正比.当2个特征值均较小时,表明目标点附近区域为“平坦区域”;特征值一大一小时,表明特征点位于“边缘”上;只有当2个特征值均比较大时,沿任何方向的移动均将导致灰度的剧烈变化.由此而得到Harris的角点响应函数R:

其中,det(M)=λ1λ2表示矩阵 M 的行列式,trace(M)=λ1+λ2表示矩阵的迹,k的取值范围是0.04~0.06.当目标像素点的R值大于给定的阈值时,该像素点即为角点.
Harris算法虽然较Moravec算子是有所改进,但是仍然存在以下不足[8-10]:①角点提取的质量和数量很大程度上取决于阈值的设定,阈值大会丢失一部分角点,阈值小会降低角点的质量,同时,对噪声也比较敏感;②检测过程中,高斯平滑函数的窗口大小不易控制,窗口过小,受噪声的影响就大,窗口大则会使角点的位置产生偏移,增加算法的计算量;③若为了降低噪声的影响,用无限光滑的高斯函数做滤波,又会由于过平滑的原因导致角点信息丢失.
2 本文的算法设计
Harris角点检测算法存在的不足,可以通过优化公式(4)来改进.公式(4)中的k值有一个取值范围,不同的k值,算法的效果也是不同的.但是现在这个角点响应函数仍然在使用,是因为如果k值能够选取恰当的话,算法也可以达到很好的效果.而这个恰当的k值的选取,要经过大量的实验进行调试验证.要避免上述问题,需要找到一个不受k值影响的响应函数来替代公式(4).
公式(4)中的响应函数R是关于自相关矩阵M的函数,与M的2个特征向量λ1λ2有关.某一个目标像素点的自相关矩阵M的2个特征值 λ1和λ2(λ1,λ2≥0 ),如果满足条件λ1≈λ2,那么的值趋于0,而且有0≤R**≤1.注意到R**和特征多项式det(λ-M)有关,且.假设R*=1-R**,仍然成立0≤R*≤1.由此可以得到关于R*的表达式:

以(5)式作为检测时的响应函数时,当R*→1时,该点可以判断为角点;当R*→0时,该点即为边缘点.但是这个表达式仍存在一些缺陷,在2个特征值相等和不相等的时候,R*值是不同的.为了避免这个问题,通常会在分母部分加上一个参数,得到一个更稳健的表达式,如下:

其中ε为任意小的正数,式(6)中没有k值,避免了因k值选择的随机性对响应函数的影响.如果其中一个特征值趋于0,那么R也将趋于0;如果2个特征值比较接近而且都比较小,R值仍然趋于0;如果2个特征向量的值都比较大时,R值就会变大.以上优化后的算法步骤如下:
Step1:对每个像素点计算相关矩阵M;
Step2:计算每个像素点的角点响应值R*;
Step3:在高斯窗口内寻找极大值,若R*大于阈值则视为角点.
本文用式(6)代替原Harris中的角点响应函数,即式(4),不仅不改变R值与每个像素点的自相关性,保留了原算法的优点,而且同一个目标点优化后的响应值和之前的响应值相比具有更高的精度,这一特性,使本文的算法在进行角点检测时,找到了之前漏检的角点,当有噪声干扰时,弱化了噪声对目标像素点的响应值的影响,从而在仿真实验中得到了更多稳定的角点,也降低了噪声对角点检测的影响.
3 实验分析
仿真实验是在Matlab 7.0的环境下运行,图1是原始图片检测到的特征点,左边是文献[3]中的Harris算法结果,右边是本文算法结果.可以看出,本文算法在提高了响应函数的精确度之后明显比原Harris算法得到了更多稳定的角点.
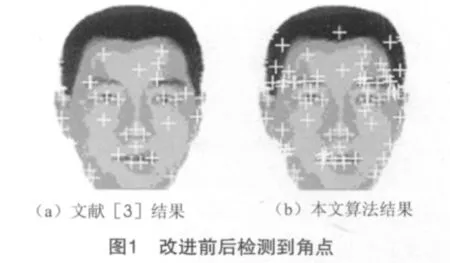
为了检测算法的抗噪性,对原始图片分别加入均值为0,方差为0.01;均值为0,方差为0.02的高斯噪声,以及叠加密度为0.04的椒盐噪声.之后用这2种算法对加入噪声后的图片进行角点检测.图2为原Harris算法检测到的角点,图3为本文算法检测到的角点.

从图2和图3可以看出,Harris算法在图像加入噪声后检测到的角点数目比加入噪声之前明显增加,而本文的算法受噪声的影响却要小的多,这一结果也在表1、2中反映出来.表1是2种算法分别对人脸图片和加入噪声后的图片检测到的角点数量.表2为噪声对2种算法的影响率(因加入噪声而多出的角点数目与原图角点数目的比率).
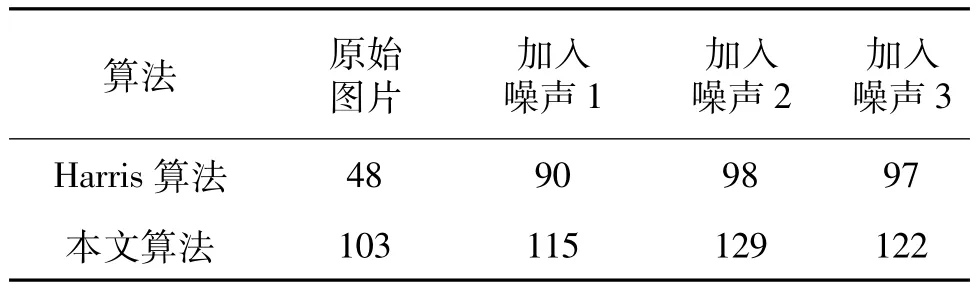
表1 2种算法检测到的角点数目
从表1和表2的比对可以看出,原Harris角点检测算法在没有噪声干扰的情况下,检测到的角点非常少,而加入噪声之后角点的数目急剧增加.经过改进之后,受噪声的影响率没有超过0.3,这比原Harris算法的影响率已经降低了很多.本文采用的角点响应函数,使每个目标点的R值降低了因加入噪声而大幅度波动的影响,在相同的阈值下,检测到更多稳定的角点的同时,也有效地体现了抗噪性能的提高.

表2 加入噪声对检测的影响率
4 结语
Harris角点检测算法在实际应用中易受噪声的干扰,已经不能满足要求.怎样得到大量的且不受噪声影响的特征点就显得很重要.本文通过改进角点响应函数,提高在检测时每个目标点的精度,在进行特征点判定时,降低了噪声的影响,一定程度了解决了上述问题.
[1]KITCHEN L,ROSENFELD A.Gray level corner detection[J].Pattern Recognition Letter,1982,3(1):95 -102.
[2]SMITH S M,BRADY M.A new approach to low level image processing[J].International Journal of Computer Vision,1997,23(1):45 -78.
[3]HARRIS C,STEPHENS M.A combined corner and edge detector[C]//Fourth Alvey Vision Conference.1998:147-151.
[4]毛雁明,兰美辉.一种改进的基于Harris的角点检测方法[J].计算机技术与发展.2009,5(5):127-129.
[5]NOBLE A.Descriptions of image surface[D].Oxford University,1989.
[6]李霞,赵宇明.基于特征的人脸分类算法研究[J].微型电脑应用.2010,26(4):60-64.
[7]邱建国,张建国,李凯.基于Harris与Sift算法的图像匹配方法[J].测试技术学报.2009,23(3):271-274.
[8]何应辉,蔡光程.角点检测的一种新方法[J].云南民族大学学报:自然科学版.2007,16(1):45-47.
[9]解洪胜,王连国.基于DT-CWT和SVM的人脸图像集成分类方法[J].云南民族大学学报:自然科学版,2010,19(5):313 -316.
[10]何应辉,蔡光程,黄晓昆.改进的基于模板的角点检测算法[J].云南民族大学学报:自然科学版,2010,19(4):309-312.
(责任编辑庄红林)
Optimization of Harris Corner Detection Algorithm
LIU Ying,ZHANG Jiu-dong,ZHOU Wei-hong
(School of Mathematics and Computer Science,Yunnan University of Nationalities,Kunming 650031,China)
This research focuses on the Harris corner detection algorithm,and finds that some corners are often influenced by noise.In this research,the response function of corner detection is optimized to avoid the influence of k.The precision of each target pixels′feature response function is improved.When used to detect face features,the experimental results show that the anti- noise ability of this algorithm is greatly enhanced if compared with the Harris corner detection.
feature detection,face recognition,noise,response function
TP 391
A
1672-8513(2011)02-0136-03
10.3969/j.issn.1672-8513.2011.02.015
2010-11-01.
云南省教育厅研究生科学研究基金(09J0061,2010J071).
刘莹(1983-),女,硕士研究生.主要研究方向:数字图像处理.
周卫红(1969-),男,硕士,副教授.主要研究方向:数字图像处理.

