基于投影法实现矩形窗口的任意曲线裁剪

李红林，兰美辉，张顺吉，杨 莉

(1.曲靖师范学院计算机科学与工程学院，云南 曲靖655011;2.云南中医学院现代教育技术中心，云南 昆明650200)

基于投影法实现矩形窗口的任意曲线裁剪

李红林1，兰美辉1，张顺吉1，杨 莉2

(1.曲靖师范学院计算机科学与工程学院，云南 曲靖655011;2.云南中医学院现代教育技术中心，云南 昆明650200)

对含有任意曲线的图像进行二值化后，针对某一矩形区域，对曲线上的点进行水平和垂直投影，投影后若在该矩形区域内(窗口内)，给予显示;否则在窗口外，裁剪掉(即不显示).该方法能动态的定义矩形窗口大小，能对任意规则曲线(如圆)和不规则曲线(如Bezier曲线、B样条曲线)进行裁剪.该方法简单、高效.

投影;矩形窗口;曲线;裁剪

裁剪问题是计算机图形学的基本问题之一.裁剪是裁去窗口之外物体的一种操作.裁剪的目的是判断图形元素是否在所考虑的区域内，如在区域内，则进一步求出区域内的那一部分［1］.常用的直线裁剪算法有Cohen－Sutherland算法［2］、中点裁剪算法、梁友栋－barskey算法［3］.工程中常用到的曲线有2种:一种是规则曲线，可以用曲线方程式来表示，例如:圆、椭圆、抛物线、双曲线、正弦余弦曲线等;另一种是不规则曲线(也称自由曲线)，此类曲线形状较复杂，不能确切给出描述整个曲线的方程，它们通常是实际测量得到的一系列离散点用曲线拟合方法来逼近的.如B样条曲线、Bezier曲线、Hermite样条曲线等.目前，研究直线、曲线、多边形的裁剪方法比较多［4－7］，但大多数方法都要求与窗口边界的交点，计算量较大，方法较复杂.本文提出基于矩形窗口的曲线裁剪方法，思想较简单，能实现任意的直线、曲线的准确裁剪.

1 规则曲线裁剪

1.1 二值化

假定:曲线的颜色为ForeColor，背景的颜色为BackClor.从上到下，从左到右逐行、逐列扫描图像中的每个像素点，分2种情况:一是该像素点的颜色是ForeColor，则分别统计其在水平、垂直方向上的像素个数，即为水平、垂直方向的投影值，如果该点的水平、垂直投影都在指定的矩形窗口内，则此点就是曲线上且在窗口内的点，应保留(不改变颜色)，否则应裁剪掉，把该点的颜色变为BackColor;二是该像素点的颜色不是ForeColor，那么说明该点不是曲线上的点，把其颜色置为BackColor.

1.2 投影法实现圆裁剪

常见的曲线裁剪的基本思想是:假设矩形窗口的最左边为RLeft，最右边为RRight，最上边为RTop，最下边为RBottom.对曲线进行裁剪，若当前点的值为RValue，根据曲线方程，判断该点是否在曲线上，如果不在，则不考虑;如果在，且RBottom≤RValue≤RTop，RLeft≤RValue≤RRight同时满足，那么说明此点在曲线上且在窗口之内，保存之;若RVuale＜RBottom或RValue＞RTop或RValue＜RLeft或RValue＞RRight，则此点在曲线上但在窗口之外，应去除;此方法，实现方法非常简单，但是需要逐点判断一个点是否在曲线上，计算量大且比较费时.

目前关于矩形窗口的圆裁剪问题常用的方法是判断一个圆是否完全在窗口内(完全可见)或是否完全在窗口外(完全不可见).如果是，则算法结束;如果不是，则把圆按一定的顺序对各边界进行裁剪［8］.此方法每进行一个窗口边就要计算该窗口边与圆的交点，并判断其是否在该边界上还是在延长线上，计算量大.孙岩等［9］结合此方法，充分利用矩形和圆的对称性提出了矩形窗口的曲线裁剪算法，能减少圆与窗口边界求交的次数，与文献［8］的方法相比，计算量一定程度上减少了.但是，此方法仍然要与窗口边界求交.本文提出的基于投影法实现矩形窗口的任意曲线的裁剪，方法简单，准确率高，同时不用计算曲线与窗口边界的交点.

投影法是沿着图像某个方向截面的灰度值累加计算量的集合.投影分为水平投影和垂直投影.对图1(a)中的圆进行水平、垂直投影分别为图1(b)、(c)，图1(a)与矩形窗口的位置关系如图2(a)，此时若圆上的某点的值为RValue，且RBottom≤RValue≤RTop，RLeft≤RValue≤Rright，则说明该点是在矩形窗口内的点，应该显示(即保留)，否则，该点是窗口外的点，不显示(即裁剪掉).图2(b)为圆被矩形窗口裁剪后的结果图.

2 不规则曲线裁剪

2.1 投影法实现三次Bezier曲线裁剪

Bezier曲线表达式为:

三次Bezier曲线，由4个点P0，P1，P2，P3可定义1条三次Bezier曲线，即n=3.可写成:

Bezier曲线方法具有很强的几何特征，在计算数学中起重要作用［10］.对图3(a)中的三次Bézier曲线，进行水平、垂直投影分别为图3(b)、(c).

基于如图4(a)的矩形窗口，直接对三次Bezier曲线进行水平、垂直投影，如图4(b)所示，投影区域分别为 RH，RV，若RLeft≤RV≤ RRight，且RBottom≤RH≤RTop，即该区域在窗口之内，把该区域所对的点恢复显示出来.否则，该区域不在窗口内，应去除，处理后如图4(c)所示.此方法不需要逐点判断是否在曲线上，方法简单，运行速度比较快.

2.2 投影法实现三次B样条曲线裁剪

B样条曲线:给定m+n+1个顶点Pi(i=0，1，2，…，m+n)，可以定义 m+1段n次参数曲线:

其中:Pk，n(t) 为第 k 段 n 次 B 样条曲线段(k=0，1，…，m);Fi，n(t) 为 n 次 B 样条基函数，其形式为:

三次 B 样条曲线(即 n=3，i=0，1，2，3)，可写成:

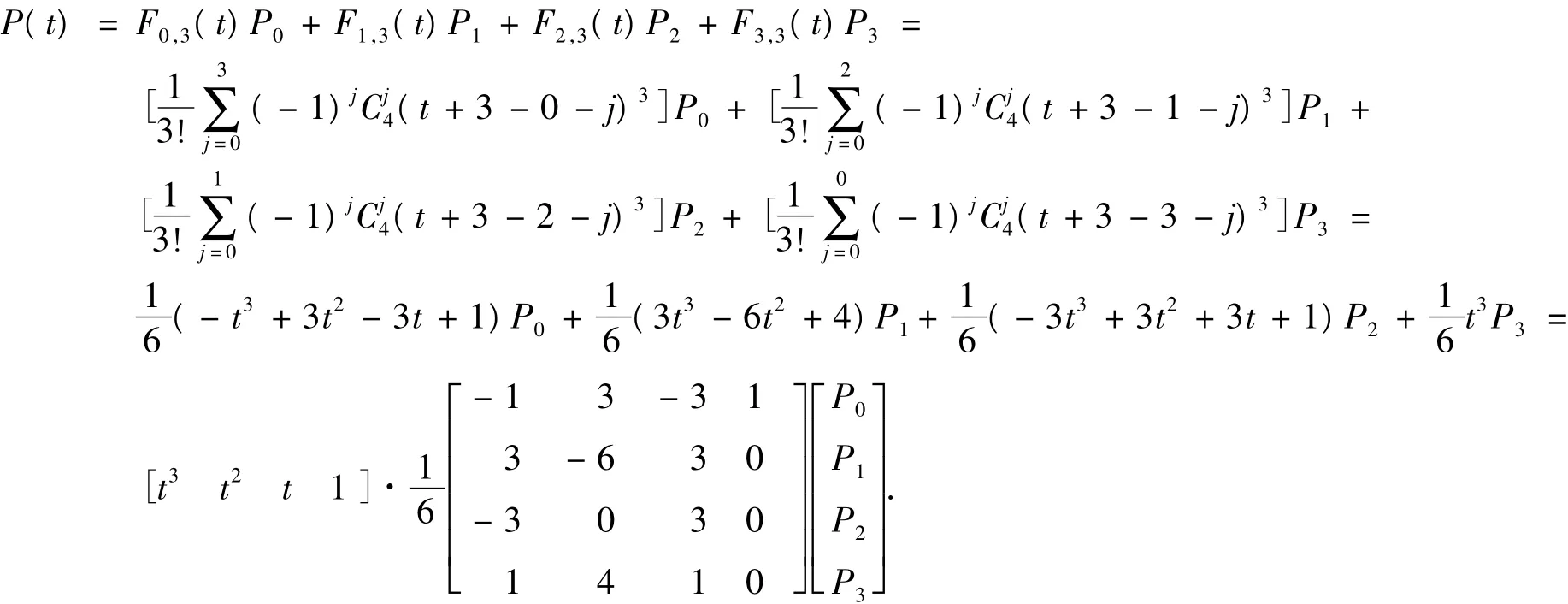
对图5(a)中的B样条曲线进行水平、垂直投影分别如图5(b)、(c)所示.

对图5(a)关于某一矩形窗口(矩形窗口的大小可以随机输入)进行水平、垂直投影，投影后在窗口内的部分说明是应保留的，显示出来;反之，在窗口外的部分应被裁剪掉，不显示.图5(a)基于某一矩形窗口的上下边界内的部分的水平投影如图6(a)所示;左右边界内的部分的垂直投影如图6(b)所示，投影值既在上下边界内又在左右边内的部分，即为在窗口内的部分(裁剪结果)，应显示，如图6(c)所示.

3 裁剪流程框图

流程图见图7.

4 结语

本文提出的方法，除了能对圆、Bezier曲线、B样条曲线裁剪外，还能裁剪任意曲线、多边形等复杂图形，同时可以动态地输入窗口的大小.方法简单，速度快，裁剪的准确率高.但是，此方法只适合于裁剪的窗口为矩形.下一步研究的重点是实现关于任意窗口的曲线裁剪.

［1］银红霞，杜四春，蔡立军，等.计算机图形学［M］.北京:中国水利水电出版社，2009.

［2］曲毅，李存华.二维线段裁剪算法的分析与探索［J］.计算机应用与软件，2006，23(7):113－114.

［3］LIANG Y D，BARSKY B A.A new concept and method for line clipping［J］.ACM Trans On Graphics，1984，3(1):1 －22.

［4］MAILLOT P G.A new，fast method for 2D polygon clipping:analysis and software implementation［J］.ACM Trans On Graphics，1992，11(15):276 －290.

［5］LIANG Y D，BARSKY B A.An analysis and algorithm for polygon clipping［J］.Communication of the ACM，1983，26(11):868 －877.

［6］赵平，冯春，李柏林.一般多边形窗口的有效线裁剪算法［J］.西南交通大学学报，2004，39(1):64－68.

［7］杭后俊，孙丽萍.任意多边形窗口的圆裁剪算法［J］.计算机技术与发展，2009，19(5):235－241.

［8］刘勇奎.计算机图形学的基本算法［M］.北京:科学出版社，2001，62－70.

［9］孙岩，唐棣.矩形窗口的曲线裁剪算法［J］.计算机应用与软件，2003，(05):35－36.

［10］于巍.随机函数的Bezier逼近问题［J］.云南民族大学学报:自然科学版，2009，18(2):117－119.

(责任编辑庄红林)

Random Clipping of Curves in Rectangular Windows Based on the Projection Method

LI Hong-lin1，LAN Mei-hui1，ZHANG Shun-ji1，YANG Li2
(1.School of Compute Science and Engineering，Qujing Normal University，Qujing 655011，China;2.Modern Education Technology Center，Yunnan University of Traditional Chinese Medicine，Kunming 650200，China)

Images with curves are binarized，and then horizontal and vertical projections are done to the points of the curves to a certain rectangular window.It aims to test whether the points are inside the rectangular region(or inside the window)or not after the projections.If they are inside the window，they should be displayed，otherwise，they should be clipped(not to be displayed).In this way the size of the rectangular window can dynamically be defined，and clipping can be done to any regular curves(for example，circles)or irregular curves(for example，Bezier curves，B － Spline curves).This method is simple and efficient.

projection;rectangular window;curve;clipping

TP 391.41

A

1672－8513(2011)02－0132－04

10.3969/j.issn.1672 －8513.2011.02.014

2010－09－16.

曲靖师范学院青年项目(2009QNO28).

李红林(1980－)，女(彝族)，讲师，硕士.主要研究方向:计算机图像处理与模式识别.