大位移钻井全井段岩屑动态运移规律

郭晓乐，汪志明，龙芝辉

(1.重庆科技学院石油天然气工程学院，重庆401331;2.中国石油大学石油工程学院，北京102249)

大位移钻井全井段岩屑动态运移规律

郭晓乐1，2，汪志明2，龙芝辉1

(1.重庆科技学院石油天然气工程学院，重庆401331;2.中国石油大学石油工程学院，北京102249)

根据固液两相流理论，综合考虑岩屑的悬浮、滚动和滑动运移方式以及悬浮层固液相速度差和钻杆旋转的影响，建立大位移井全井段三层岩屑动态运移模型，用于模拟计算实际钻井中正常钻进和停钻循环的全部过程;基于有限体积法原理，引入SETS方法对模型进行数值求解，并进行模拟分析。结果表明:对于具有长斜井段的大位移井，环空岩屑床分布达到稳定状态需要很长时间，使用稳态模型计算环空岩屑床高度和压力会产生较大误差;排量对岩屑床形成速度影响较大，排量越小，环空达到稳定状态时形成的岩屑床越高，环空达到稳定所需时间越长;排量对岩屑床冲蚀速度影响较大，而初始岩屑床高度对完全清洗井眼所用时间影响不大。所建模型计算结果与试验回归模型计算结果吻合较好，从而验证了所建模型的正确性和广泛的适应性。

大位移井;岩屑运移;动态模型;实钻模拟

井眼清洁是大位移钻井顺利进行的关键技术之一，其核心是了解环空岩屑运移规律。现有岩屑运移模型主要分为稳定［1-10］和不稳定模型［11-12］，在分析岩屑运移规律方面取得了一定成果，但仍然存在不足:第一，从理论上来说不稳定模型更接近实际岩屑运移过程，但计算复杂，不适合工程应用，而稳定模型无法描述岩屑在环空中运移和累积的实际过程，这在大斜度井段较长时(大位移井)将会产生较大误差;第二，现有模型除了经验模型和试验数据回归模型外，均没有考虑钻杆旋转的影响，而钻杆旋转对于岩屑运移有很大影响;第三，现有模型均是针对某一井段，例如对直井段、斜井段或水平段进行研究，没有将整个大位移井作为一个整体进行研究，不能描述岩屑在大位移井全井段连续运移的过程。因此，这些模型在工程应用时存在一定的局限性。笔者根据固液两相流理论，在已建立的大位移井大斜度井段三层稳定模型［9］和两层不稳定模型［12］的基础上，综合考虑岩屑的悬浮、滚动和滑动运移方式以及固液相速度差和钻杆旋转的影响，建立大位移井全井段三层岩屑动态运移物理和数学模型，用于全井段(直井段、斜井段和水平段)计算，并模拟计算实际钻井中正常钻进和停钻循环的全过程。

1 模型的建立

假设在一定条件下环空中形成三层岩屑运移模式，包括上部的悬浮层、底部的均匀岩屑床层和中间的分散岩屑床层，各层之间存在质量和动量交换。与两层模型相比，三层模型可以描述绝大部分环空岩屑运移形态。在同一工况下，不同时间、不同井段可能会存在不同的岩屑分布形态，因此本文中建立的三层动态模型旨在实时计算和模拟不同时间、不同位置处的岩屑运移形态，为大位移井井眼清洁和水力参数计算提供理论指导。

图1为大位移井三层模型岩屑分布及各层受力示意图。由于研究和计算的问题较为复杂，因此假设:①固液两相为不可压缩流体，除悬浮层外，不考虑其他各层内固液两相之间的滑动;②钻井液和岩屑物性连续，钻井液流变模式为幂律模式;③悬浮层岩屑体积分数相对很小，且符合扩散定律;④均匀层岩屑体积分数为55%，分散层岩屑体积分数为均匀层的0.8倍。

图1 大位移井三层模型示意图Fig.1 Schematic diagram of three-layer model of extended reach well

将流体力学基本原理和方程应用于各层(悬浮层固相、悬浮层液相、分散层和均匀层)，可以得到所需的基本方程。

连续性方程为

式中，ρ为密度，kg/m3;C为体积分数;A为截面积，m2;U为速度，m/s;Φe、Φd和Φdb分别为分散层进入悬浮层的量、悬浮层沉降量、分散层与均匀层交换量，kg/s/m;下标h、s、f、d和b分别表示悬浮层、悬浮层固相、悬浮层液相、分散层和均匀层。

动量方程为

式中，p为压力，Pa;θ为井斜角，(°);τhs、τhf、τd和τb分别为悬浮层固相、悬浮层液相、分散层和均匀层流体切应力，N/m2;τhd和τdb分别为悬浮层与分散层、分散层与均匀层界面切应力，N/m2;Shw、Sdw和Sbw分别为悬浮层、分散层、均匀层与壁面接触湿周，m;Shd和Sdb分别为悬浮层与分散层、分散层与均匀层接触湿周，m;Fsf、Fdw、Fbw和Fdb分别为悬浮层固液相之间、分散层岩屑与井壁、均匀层岩屑与井壁、分散层与均匀层岩屑之间的摩擦力，N/m。

模型共包含8个方程、8个未知数，所要求解的未知数为Cs、Us、Uf、Ud、Ub、p、Ad和Ab，为使方程可以求解，还需要一些辅助方程。辅助方程包括几何关系式和其他各力或变量的求解公式。

2 钻杆旋转的处理及模型求解

研究和实践表明，钻杆旋转有利于携岩，但由于钻杆旋转对岩屑运移的影响机制比较复杂，目前并没有很完善的模型可以描述其影响。本文中对其进行简化处理，将悬浮层流体速度修正为流体轴向返速与钻杆旋转引起的流体切向线速度的矢量和，相当于钻杆旋转增加了悬浮层流体速度值。悬浮层流体速度增加，一方面会增加悬浮层岩屑运移量，另一方面通过界面剪切力也会增加分散层的速度和高度、岩屑运移量，从而增加总的环空岩屑运移量，这样可以在一定程度上描述钻杆旋转对岩屑运移的影响。同时，通过使用当量偏心距［13］修正钻杆旋转带来的线速度，以此描述偏心对岩屑运移的影响。

钻杆旋转带来的线速度Ur可以表示为

其中

式中，Dw为井径，m;ha为偏心环空当量间距，m;Rpm为钻杆转速，rad/s;Dpo为钻柱外径，m;e为偏心间距，m;E(2e/Dw，π/2)为第二类椭圆积分。

悬浮层流体当量速度Ufc可以表示为

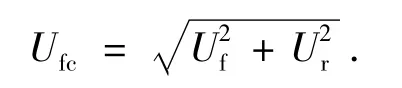
由于方程为强非线性方程组，未知数多且相互耦合，使用SIMPLE方法［14］求解效率较低，因此经过调研引入SETS(stability enhancing two step)方法求解。SETS方法包括预测和修正两步，在每一时间步无须迭代，因此能够有效提高计算效率。

3 动态井底与实钻模拟

现有岩屑运移不稳定模型大多假设钻头位置不动，这显然与实际情况不符，因此通过虚拟网格来模拟实际钻进过程，其思路为在全部井深上划分网格，在钻头钻至该网格前，该网格为虚网格，其中各参数均为0，当钻至该网格时，将该网格设为边界网格并赋初值。当全部井深钻完后，停钻并使用同一排量开始洗井。

由于各参数对稳态岩屑床高度影响规律的理论和试验研究较多，因此主要分析钻井环空岩屑的动态运移过程。

假定一口井的井身结构如图2所示，其中0～250 m为直井段，0.25～1 km为造斜段，井斜角从0°连续变化到90°，1～2 km为水平段，全井垂深800 m。大位移井钻井实践表明，216 mm井眼段虽然也是大斜度井段，但由于井眼尺寸小，泵排量可以满足要求，因此该井段一般不会出现携岩问题，而311 mm井眼段同样是大斜度井段，由于环空尺寸大，泵排量一般达不到携岩要求，导致该井段钻进时携岩问题最为突出。因此，重点模拟311 mm井眼岩屑运移情况，使用127 mm钻杆，钻井液密度为1.1 g/cm3，岩屑密度为2.5 g/cm3，岩屑粒径为5 mm，钻井液性能参数为n=0.5，K=0.5 Pa·sn，钻杆转速为90 r/min，机械钻速为30 m/h，偏心度为0.5。

图2 井深结构示意图Fig.2 Schematic diagram of wellbore configuration

3.1 实钻岩屑床运移

假定从测深1.1 km钻进至2 km，然后停钻洗井，不同排量时钻进和停钻洗井模拟结果如图3所示。图中岩屑床相对高度Hc=100(yd+yb)/Dw。

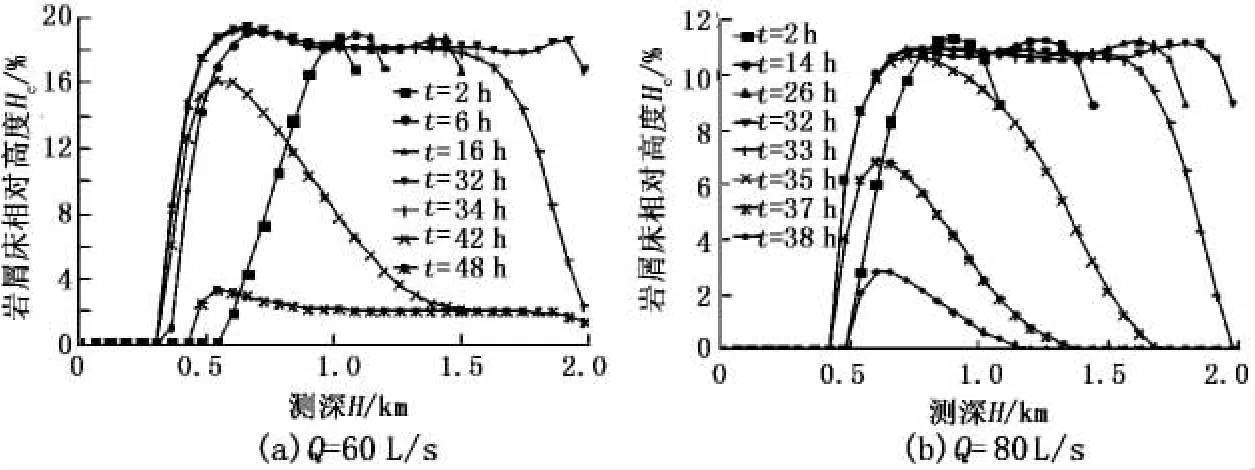
图3 实钻岩屑床变化Fig.3 Cuttings bed variation while drilling

从图3可以看出，钻头逐渐后移，使用60 L/s排量经过32 h后钻进完成，环空形成18.5%相对高度的岩屑床，清除此岩屑床约需洗井16 h，使用80 L/s排量经过32 h后钻进完成，环空形成11.1%相对高度的岩屑床，清除此岩屑床约需洗井6 h。由此看见，排量增加将降低环空岩屑床高度，缩短岩屑床达到稳定和清除岩屑床时间。另外，从图中也可以看出，斜井段岩屑床要略高于水平段的。

3.2 岩屑床冲蚀时间

假定以60 L/s的排量钻进完成后环空形成10%相对高度的岩屑床，之后开始洗井，则岩屑床冲蚀过程如图4所示。清除此岩屑床约需14 h。对比图3可以看出，增加排量能有效减少完全洗井时间。初始岩屑床高度对完全洗井时间影响不大，这可能是因为岩屑床高度越大，悬浮层速度越大，导致岩屑床运移速度增大，从而总的运移时间基本不变。国外Martins［11］的试验也发现了这一点。

图4 排量为60 L/s时岩屑床的冲蚀Fig.4 Cuttings bed variation while flushing at flow rate of 60 L/s

3.3 钻杆旋转

钻杆旋转对岩屑床冲蚀的影响如图5所示。从图中可以看出，钻杆旋转能够有效降低环空岩屑床高度，随转速增加，环空岩屑床高度减小，而减小的幅度随钻杆转速的增加而逐渐减小。

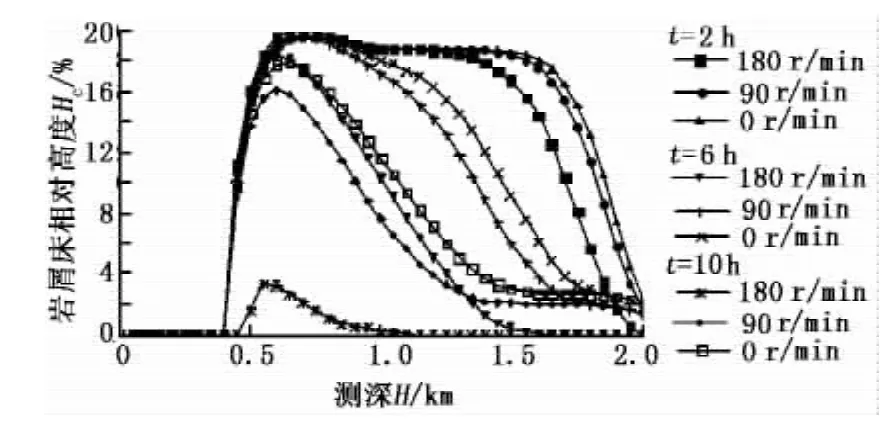
图5 钻杆旋转对岩屑床高度的影响Fig.5 Influence of drillpipe rotation on cuttings bed height

3.4 实钻井底压力和当量循环密度变化

实钻过程中井底压力和当量循环密度的变化过程如图6所示。从图中可以看出，在钻进过程中，井底压力和环空压耗逐渐增加，而洗井时逐渐减小。考虑岩屑运移的影响，随排量增加，井底压力和当量循环密度反而减小，这是由于排量增加，环空岩屑体积分数和岩屑床高度减小，环空固相压耗减小。当排量增加所带来的流体压耗增幅大于环空固相压耗降幅时，随排量增加，井底压力和当量循环密度增加。因此，可以推测存在一最优排量，在此排量下井底压力和岩屑床高度同时相对较小。

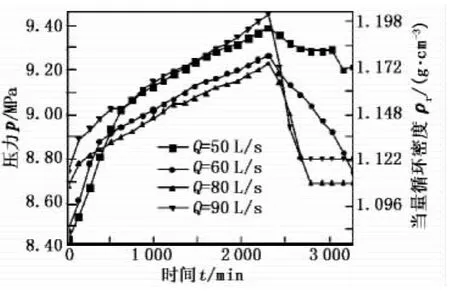
图6 实钻过程中井底压力变化规律Fig.6 Bottom hole pressure variation while drilling

4 模型对比

4.1 与稳定模型的对比

汪海阁［10］根据试验数据得到回归公式，可以用其对理论模型进行验证。图7为本文中模型计算的岩屑床相对高度与回归公式计算结果的对比。

图7 模型计算结果与岩屑床高度回归公式结果对比Fig.7 Contrast of model results with the results of regression formula of cuttings bed height

本文中计算出的稳态岩屑床相对高度变化趋势与回归公式一致，都表现为随排量增加岩屑床相对高度减小。回归公式没有考虑环空尺寸的影响，而研究表明环空尺寸增加不利于携岩，因此考虑环空尺寸时计算出的岩屑床相对高度大于回归公式计算值。如果去除环空尺寸的影响，则本文中模型计算出的结果与汪海阁回归公式非常吻合，从而验证了本模型的正确性。

4.2 与不稳定模型对比

Martins的两层不稳定模型［11］考虑因素比较简单，没有考虑悬浮层岩屑运移，也没有考虑岩屑床表层岩屑的滚动、滑动运移，因此相同条件下计算出的岩屑床高度要比本文中模型的大。对比时将本文模型简化，不考虑悬浮层和分散层岩屑运移，使用与Martins计算同样的工作参数，其计算结果为:本文中模型和Martins模型最终形成的岩屑床相对高度分别为8.2%和8.1%，达到稳定所需要的时间分别为5900 s和6000 s，可见两者基本吻合。这一方面验证了本文模型的正确性，另一方面也说明所建三层不稳定模型具有较强的适应性，可以根据需要简化为不同类型(考虑或不考虑悬浮层岩屑运移)的两层不稳定模型。

5 结论

(1)建立的大位移井全井段三层岩屑动态运移模型能够模拟正常钻进和停钻循环的实际过程，为钻井岩屑运移模拟和水力参数计算提供了依据。

(2)对于具有长斜井段的大位移井，环空岩屑床分布达到稳定状态需要很长时间，使用稳态模型计算环空岩屑床分布和压力会产生较大误差。

(3)排量对岩屑床形成速度影响较大，排量越小，环空达到稳定状态时形成的岩屑床高度越高，环空达到稳定状态所需时间越长。

(4)排量对岩屑床冲蚀速度和洗井时间影响较大，而初始岩屑床高度对洗井时间影响不大。

(5)考虑环空岩屑运移的影响，随排量增加，井底压力和当量循环密度先减小后增加，存在一最优排量，在此排量下井底压力和岩屑床高度相对较小。

［1］DORON P，GRRANICA D，BARNER D.Slurry flow in horizontal pipes—experimental and modeling［J］.Int J Multiphase Flow，1987，13(4):535-547.

［2］GAVIGNET A，SOBEY I.Model aids cuttings transport prediction［J］.JPT，1989，9:916-921.

［3］DORON P，BARNER D.A three-layer model for solidliquid flow in horizontal pipes［J］.Int J Multiphase Flow，1993，19(6):1029-1043.

［4］DORON P，SIMKHIS M，BARNER D.Flow of solid-liquid mixtures in incline pipes［J］.Int J Multiphase Flow，1997，23(2):313-323.

［5］NGUYEN D，RAHMAN S S.A three-layer hydraulic

program for effective cuttings transport and hole cleaning in highly deviated and horizontal wells［R］.SPE 36383，1996.

［6］HYUN Cho，SHAH Subhash N，OSISANYA Samuel O.A three-layer model for cuttings transport with coiled tubing horizontal drilling［R］.SPE 63269，2000.

［7］汪志明，张政.水平井两层稳定岩屑传输规律研究［J］.石油大学学报:自然科学版，2004，28(4):63-66.WANG Zhi-ming，ZHANG Zheng.A model for two-layer cutting transport in horizontal well［J］.Journal of the University of Petroleum，China(Edition of Natural Science)，2004，28(4):63-66.

［8］汪志明，张政.大斜度井两层稳定模型岩屑传输规律研究［J］.石油钻采工艺，2003，25(4):8-10.WANG Zhi-ming，ZHANG Zheng.Study on cuttings transportation tendency of the dual layer stabilizing model in highly inclined well［J］.Oil Drilling＆Production Technology，2003，25(4):8-10.

［9］郭晓乐，汪志明.大位移井岩屑运移规律研究［C］//朱德祥，周连第，杨显成，等.第二十届全国水动力学研讨会文集.北京:海洋出版社，2007:552-557.

［10］汪海阁，刘希圣，丁岗，等.水平井段岩屑床厚度模式的建立［J］.石油大学学报:自然科学版，1993，17(3):25-32.WANG Hai-ge，LIU Xi-sheng，DING Gang，et al.The model of cuttings bed thickness in horizontal well section［J］.Journal of the University of Petroleum，China(Edition of Natural Science)，1993，17(3):25-32.

［11］MARTINS A L，SANTANA M L，CAMPOS W，et al.E-valuating the transport of solids generated by shale instabilities in ERW drilling［J］.SPE/DC，1999，14(4):254-259.

［12］汪志明，张政.大位移水平井两层不稳定岩屑传输模型研究［J］.水动力学研究与进展:A辑，2004，19(5):676-681.WANG Zhi-ming，ZHANG Zheng.A two-layer time-dependent model for cuttings transport in extended-reach horizontal wells［J］.Journal of Hydrodynamics(ser A)，2004，19(5):676-681.

［13］刘永建，陈家琅.偏心环空中幂律流体轴向层流压降的计算［J］.石油钻采工艺，1989，11(5):9-15.LIU Yong-jian，CHEN Jia-lang.Pressure loss calculation of laminar flow of power law fluids in eccentric annulus［J］.Oil Drilling＆Production Technology，1989，11(5):9-15.

［14］MAHAFFY J H.A stability-enhancing two-step method［J］.J Computational Physics，1982，46(3):329-334.

(编辑 李志芬)

Transient cuttings transport laws through all sections of extended reach well

GUO Xiao-le1，2，WANG Zhi-ming2，LONG Zhi-hui1
(1.College of Oil and Gas Engineering in Chongqing University of Science and Technology，Chongqing 401331，China;2.College of Petroleum Engineering in China University of Petroleum，Beijing 102249，China)

Based on the theory of solid-liquid flow，a three-layer transient cuttings transport model for all sections of extended well was developed，and the mechanisms of suspension，rolling and sliding of cuttings，the relative velocity between solid and liquid in suspension layer and the effect of drill pipe rotation were all taken into account.The model was used for calculating and stimulating all sections and processes on actual drilling and circulating conditions.The model was solved numerically by SETS method on the basis of the finite volume method theory，and some simulation cases using actual field data were made.The results show that it takes a long time to reach steady state for cutting bed transport because of long inclined wellbore of extended reach well，which leads to a big error by using steady models to calculate cuttings height and annular pressure.Pump rate has a great effect on the speed of cuttings bed formation，that is，the smaller pump rate，the higher steady cuttings bed height and the longer time to reach steady state is.Pump rate also has a deep effect on the speed of cuttings bed erosion，while the original cuttings bed height has little effect on the time of cleaning hole entirely.Finally the calculated results by this model agree well with the results of models obtained by experimental data，which indicates the validity and applicability of this model.

extended reach well;cuttings transport;transient model;actual drilling simulation

TE 21

A

10.3969/j.issn.1673-5005.2011.01.014

2010－01－24

国家科技重大专项课题(20085056－02－03－06)

郭晓乐(1981－)，男(汉族)，河南偃师人，讲师，博士，主要从事井筒复杂流动与井眼清洁技术研究。

1673-5005(2011)01-0072-05