自动生成四边形网格的方法及其在数值模拟中的应用

修荣荣,徐明海,黄善波

(1.中国石油大学期刊社,山东东营257061;2.中国石油大学储运与建筑工程学院,山东青岛266555)

自动生成四边形网格的方法及其在数值模拟中的应用

修荣荣1,2,徐明海2,黄善波2

(1.中国石油大学期刊社,山东东营257061;2.中国石油大学储运与建筑工程学院,山东青岛266555)

采用间接方法生成四边形网格,首先利用改进的两点前沿推进法把计算区域剖分成三角形网格,然后采用插点和细分的技术生成单元全部是四边形的网格,通过边互换、删点和局部插点技术进一步光滑平顺,得到适用于数值计算的网格。剖分结果表明,该方法能够在任意二维平面区域内自动生成全四边形网格,并能生成光滑过渡的局部加密网格和贴体性较好的边界层网格。该方法具有算法简单,计算量少的特点。利用所生成的网格对计算传热学中的典型算例-方腔自然对流进行求解,计算结果与基准解吻合,网格质量能够满足数值分析计算的要求。

二维区域;全四边形网格;三角形合并;变密度网格;数值模拟

在二维区域生成非结构化网格的方法中,三角形网格的自动生成算法最为成熟,但有限元计算表明,在相同网格步长下,三角形单元的计算精度不如四边形单元[1]。Aziz等[1]研究表明,有限容积法数值计算结果的精度与单元形状关系不大,与网格步长关系则极为显著。在同样网格节点分布的情况下,三角形单元的数目是四边形单元的两倍,因此,最终形成的线性代数方程组的阶数也是两倍。这样,无论是存储还是求解,都是不经济的。因此,为了在一定计算工作量的条件下尽量提高精度,提出了采用非结构化四边形网格计算思想,进而导致了四边形网格生成的技术问题。生成四边形网格的方法很多[2-8],按照单元生成方法大致分为两类:直接法和间接法。直接法[2-3,8]包括几何分割法和前沿推进法,其生成的网格质量高,不规则节点少,但在网格生成的过程中需要进行交叉检验和局部光滑(如paving方法[3]),网格生成速度较慢。相对而言,间接法的操作都是局部的,且不必进行交叉检测,因而网格生成的速度快。间接法[4-5,7]包括插入节点法和合并三角形法[5]。前者能把三角形网格完全转化为四边形网格,但插入的节点导致大量不规则单元,网格单元质量较差;后者提高了单元的质量,但不能保证把所有的三角形单元转换成四边形单元。为克服残留三角形问题,文献[6]对其作了进一步的改进,可以把三角形网格完全转化为四边形网格,且可实现局部加密,保证网格质量,但由于用布点法生成三角形网格,生成的变密度网格不够光滑。笔者基于两点前沿推进法[9]首先将计算区域剖分成三角形网格,并通过函数直接给出背景网格的信息来控制网格的疏密,然后再将三角形网格合并成四边形网格,以改进网格质量。

1 网格生成算法

生成四边形网格的算法基于三角形网格生成过程,经过拆分和局部优化,把三角形网格转化为四边形网格。

1.1 三角形网格的生成

采用改进的两点前沿推进算法生成三角形网格[9]。设边界上指定点处的四边形网格划分尺寸为h,则在三角形网格划分时离散尺寸为2h[6]。为克服文献[6]由于采用布点法控制网格步长而导致变密度网格不够光滑的缺点,引入了通过函数直接给出背景信息的处理方法[10],先生成变密度的三角形网格,从而得到光滑过渡的变密度网格,使人为的工作量和计算量大大减少。方法的基本原理是利用电荷产生的势函数随距离衰减的规律作为网格步长变化的控制函数,再结合电荷产生的势场可叠加的原理,通过多个点的网格背景信息,实现网格步长的任意加密,通过适当布置一定数量和种类的基本解作为网格步长控制函数,替代传统的背景网格,可以节省网格步长控制搜索时间,进而提高网格生成速度。

1.2 四边形网格的生成

四边形网格生成的步骤如下:

(1)合并三角形。对三角形单元的集合T中任一单元ABC,与其共边的三角形最多有3个,分别计算三角形ABC与它们合并后所得四边形的网格质量(记为β),取最大值所对应的三角形为候选合并三角形。若β值大于等于0,则执行合并操作,将四边形加到四边形集合Q中;否则不予合并,将三角形ABC加到残留三角形集合Tr中。重复此过程,直至集合T为空集。

(2)三角形的细分。由于三角形合并成四边形时总有残留三角形存在,这些三角形无法与其相邻三角形合并成四边形。为生成四边形,在三角形的形心处插入一点,与其三边中点相连,形成3个四边形,但这样破坏了其相邻四边形的拓扑结构,为此需要将三角形合并而成的四边形也要细分一次,以满足网格的拓扑要求。

(3)四边形的细分。对集合Q中的每一个四边形ABCD,将其形心O与各边中点连接,形成四个小四边形。

对于剩余的三角形处理过程如图1所示。可以看出,这种方法可以把三角形网格完全转化为四边形网格。因为原来步长为2h,所以细分后步长恰好满足要求。

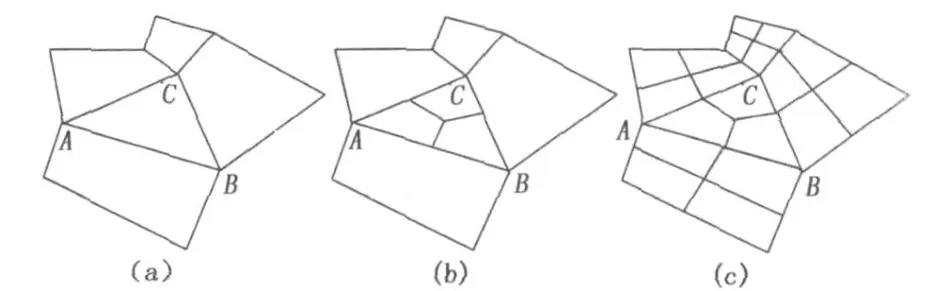
图1 剩余三角形的细分及网格处理过程Fig.1 Subdivision of residual triangles and mesh proceesing procedure

2 网格质量的改进

2.1 四边形的质量判断准则

如图2(a)所示,按逆时针走向的四边形ABCD被对角线AC分成两个三角形ABC和ACD,其质量用α表示,分别为同时,四边形又可被对角线BD分成两个三角形ABD和BCD,其α值分别为按降序重新排列成为α1,α2,α3,α4,即α1≥α2≥α3≥α4,则四边形ABCD的质量判断准则[11]为

其中,按逆时针走向的三角形ABC(图2(b))的质量按下式计算:

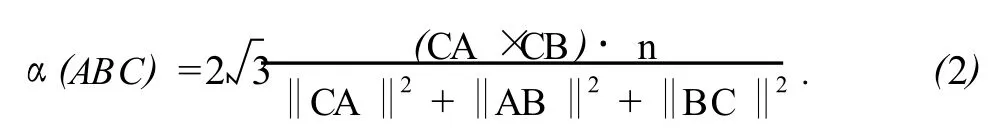
式中,n为三角形单位法向。α的最大值为1,所对应的三角形为等边三角形,α值越小,三角形质量越差。

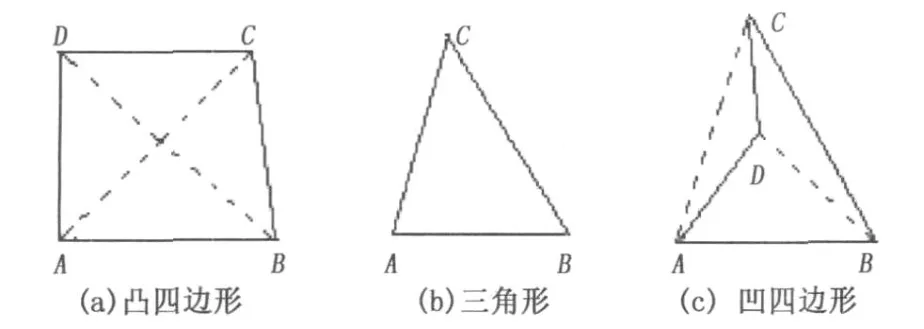
图2 凸四边形、三角形和凹四边形示意图Fig.2 Convex quadrilateral,triangle and concave quadrilateral

对于凸四边形(图2(a)),β的值在0和1之间,矩形的值最大为1。凹四边形(图2(c))的β值小于0。因此,可认为β的值越小四边形质量越差。

2.2 网格的优化光顺

最终网格质量的优劣对数值结果的精度和收敛性至关重要,生成高质量网格的一个重要措施就是进行网格后处理,即网格优化[12]。网格的优化分两步进行:局部优化[13]和整体光顺。

(1)局部优化。由于三角形内插入一点形成的四边形的单元质量较差,故在经过网格光顺处理后,还需要进一步处理以提高单元质量。四边形网格中的每个内节点的最佳相邻单元数为4,这样与其相关的单元接近于矩形。如果相邻单元数(设为Ne)远远大于或小于4,即那么以该内节点为顶点的四边形必然有不规则的。为此,对满足下列条件的单元进行删除:一个单元的两相对节点A、C都是可动节点,且相邻单元数都为3,如图3所示。

图3 单元删除Fig.3 Element deletion

(2)网格的整体光顺。采用Laplace法进行光顺处理可以改善网格的质量。光顺的本质是移动内部网格节点的位置,使其处于有共享此点的四边形单元所组成的多边形的中心。光顺处理是以改善局部最差四边形为标准,即对任一内部节点D(x,y),与其相连的四边形最小β值为βmin,假设经光顺后的节点为D＊(x＊,y＊),与其相连的四边形最小β值为则用D＊(x＊,y＊)代替D(x,y),否则不做处理。

3 剖分算例

对单连通区域和多连通区域等不规则区域进行了剖分,经过光滑后的剖分结果如图4所示。从图中可以看出,可以生成均匀网格、光滑过渡的局部加密网格和贴体性较好的边界层网格。

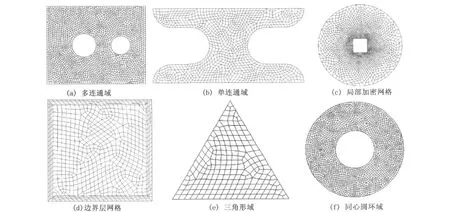
图4 剖分实例Fig.4 M esh generation results

4 数值模拟算例

利用上述方法生成的网格,计算了已有比较一致结果的方腔自然对流及半圆形空腔内的自然对流问题,对剖分的网格进行了考核,并与三角形网格进行了对比。

4.1 方腔自然对流

采用网格步长相同的三角形网格与四边形网格分别对Ra=103,104,105,106进行求解。三角形网格的节点数为1598,单元数为3050;四边形网格的节点数为1977,单元数为1896。

4.1.1 计算精度的对比

将两种网格计算所得的平均努塞尔(Nusselt)数及其对应的位置与文献[14]认为最好的解进行比较,比较结果见表1。其中,局部努塞尔数(N u)与热壁上的平均努塞尔数按下式进行计算:

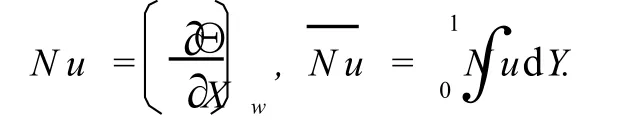
表1中数据表明,在单元边长基本相同的情况下,四边形网格的计算精度优于三角形网格,尤其是最大、最小努塞尔数和对应的位置方面。

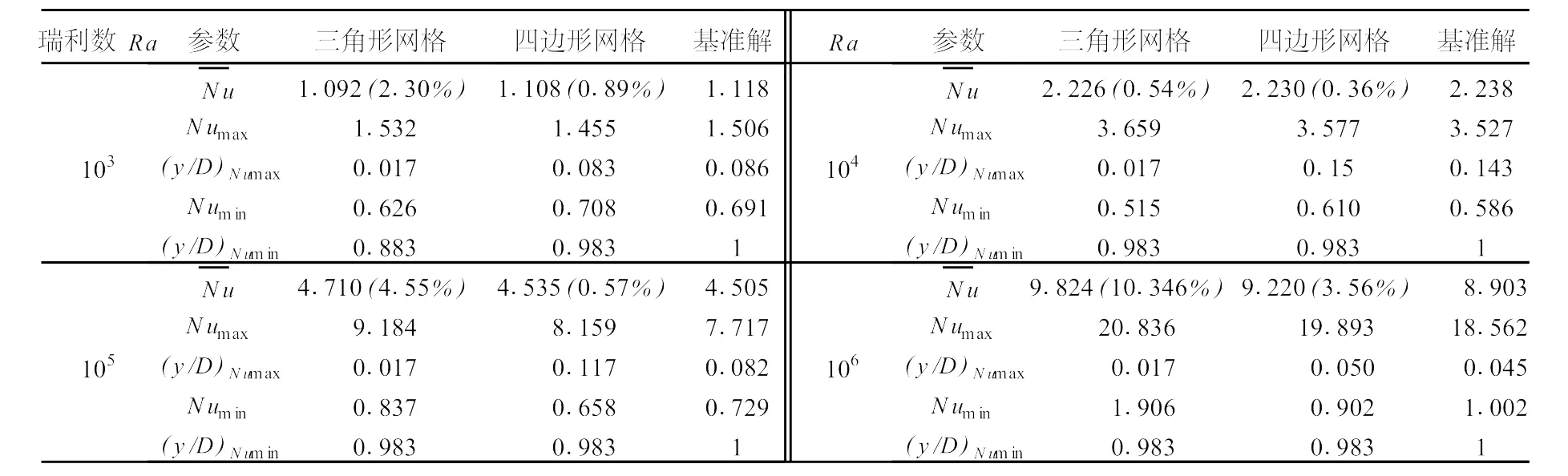
表1 努塞尔数计算结果与基准解的比较Table 1 Comparison of calculated results of Nusselt number and reference results

4.1.2 收敛特性的对比

收敛特性曲线如图5所示。图5(a)中三角形网格的节点数为710,单元数为1322,四边形网格的节点数为753,单元数为704;图5(b)中三角形网格的节点数为1598,单元数为3 050,四边形网格的节点数为1637,单元数为1 564。由图中可以看出,网格步长相同时,四边形网格的收敛速率明显高于三角形网格。

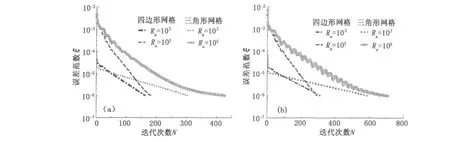
图5 收敛速率的比较Fig.5 Comparison of convergence rate

4.1.3 所耗机时的对比

两种网格的网格节点数与占用机时的关系曲线见图6。从图中可以看出,网格节点数相同时,四边形网格所耗机时远小于三角形网格,而且网格节点数越多,节省时间越明显。

4.2 半圆形空腔内的自然对流

采用四边形网格(节点数为811,单元数为758)计算出Ra=104,105时热边界上努塞尔数的分布曲线(图7),图中热壁上X值的范围为0.15≤X≤0.85。可以看出,本文的计算结果与文献[15]是一致的。

5 结束语

本文中提出的四边形网格生成方法具有计算量少、程序量少且易编制的特点,能够在任意二维平面区域生成全四边形网格,可以灵活地实现网格的局部加密,特别适合自适应网格计算的要求。利用所生成的四边形网格对计算传热学中的两个典型算例的求解结果与基准解一致,说明网格质量能够适应数值分析计算的要求。

[1] AZIZ K.Reservoir simulation grids:opportunities and problems[R].SPE 25233,1993.

[2] 赵熠,赵建军,张新访.前沿法生成四边形网格的改进方法[J].计算机工程与应用,2002(9):64-66,98.ZHAO Yu,ZHAO Jian-jun,ZHANG Xin-fang.Generating quadrilateral mesh based on the improved advancing front method[J].Computer Engineering and Applications,2002(9):64-66,98.

[3] BLACKER TD,MARK S S.Paving:a new approach to automated quadrilateral mesh generation[J].International Journal For Numerical Methods in Engineering,1991,32(4):811-847.

[4] 冯道雨,陈尚法,陈胜宏.复杂区域生成四边形网格的一种改进方法[J].岩土力学,2004,25(6):917-921.FENG Dao-yu,CHEN Shang-fa,CHEN Sheng-hong.A new quadrilateral mesh generation method based on advancing front technique[J].Rock and Soil Mechanics,2004,25(6):917-921.

[5] LO S H.Generating quadrilateral elements on plane and over curved surfaces[J].Comput Struct,1989,31:421-426.

[6] 顾元宪,马正阳,关振群.平面任意区域四边形网格自动生成的一种方法[J].计算机辅助设计与图形学学报,1998,10(5):432-439.GU Yuan-xian,MA Zheng-yang,GUAN Zhen-qun.A method of automatic generation of quadrilateral element meshes on arbitrary plane domain[J].Journal of Computer Aided Design&Computer Graphics,1998,10(5):432-439.

[7] 刘晶,聂玉峰,苏少普.四边形网格间接生成方法[J].计算机工程与应用,2010,46(2):44-47.L IU Jing,N IE Yu-feng,SU Shao-pu.Indirect method of quadrilateral mesh generation[J].Computer Engineering and Applications,2010,46(2):44-47.

[8] 李毅,鲍劲松,金烨,等.二维域多约束四边形有限元网格生成算法[J].计算机辅助设计与图形学学报,2008,20(4):488-493.L I Yi,BAO Jin-song,J IN Ye,et al.Quadrilateralmeshgeneration algorithm for planar domain with multi-constraints[J].Journal of Computer Aided Design&Computer Graphics,2008,20(4):488-493.

[9] 修荣荣,徐明海,黄善波,等.二维区域三角形的一种改进的前沿推进法[J].石油大学学报:自然科学版,2003,27(5):73-75,80.X IU Rong-rong,XU Ming-hai,HUANG Shan-bo,et al.An improved triangulation method for arbitrary two-dimensional planar domain using advancing method[J].Journal of the University of Petroleum,China(Edition of Natural Science),2003,27(5):73-75,80.

[10] 武洁,冯晋利.三角形网格生成方法中一种提供背景信息的方法[J].计算机辅助设计与图形学学报,1999,11(4):300-303.WU Jie,FENG Jin-li.The background inforrnation in advancing-front method for the triangle meshing[J].Journal of Computer Aided Design&Computer Graphics,1999,11(4):300-303.

[11] LEE C K,LO S H.A new scheme for the generation of a graded quadrilateral mesh[J].Comput Struct,1994,52:847-857.

[12] 陈立岗,郑耀,陈建军.全四边形有限元网格的拓扑优化策略[J].计算机辅助设计与图形学学报,2007,19(1):78-83.CHEN Li-gang,ZHENG Yao,CHEN Jian-jun.Topological improvement for quadrilateral finite element meshes[J].Journal of Computer Aided Design&Computer Graphics,2007,19(1):78-83.

[13] ZHU J Z,ZIENKIEW ICZ O C,H INTON E,et al.A new approach to the development of automatic quadrilateral mesh generation[J].Int J Numer Meth Engng,1991,29:1551-1567.

[14] Devahl DAV IS G,JONES I P.Natural convection in a square cavity,A comparison Exercise[M]//LEW IS R W,MORGAN K,SCHREFLER B A.Numerical methods in thermal problems.Swansea,U K:Pineridge Press,1981:552-572.

[15] VO ILKER S,BURTON T,VANKA S P.Finite-volume multigrid calculation of natural-convection flows on unstructured grids[J].Numerical Heat Transfer(PartB),1996,30:1-22.

(编辑 韩国良)

Automatic generation method of quadrilateral meshes and its application to numerical simulation

XIU Rong-rong1,2,XU Ming-hai2,HUANG Shan-bo2

(1.Periodical Office of China University of Petroleum,Dongying257061,China;2.College of Storage&Transportation and Architectural Engineering in China University of Petroleum,Qingdao266555,China)

Quadrilateral meshes on arbitrary 2D domain were generated by using indirect method.Firstly,triangle meshes were generated by improved two-point advancing method.Then by means of inserting nodes and subdivison technique,the mesh elements were composed with quadrilaterals completely.The edge interconversion,node elimation and inserting node locally were used to smooth meshes,and the meshes suitable to numerical calculation were obtained.The proposed method is characterized by its simplicity and ease of implementation.Mesh generation results demonstrate the robustness of the method.The method can also generate smooth graded quadrilateral mesh and body-fitted boundary layer meshes.The generated meshes were used to solve natural convection in a square cavity.The solution results agree well with the reference results.The quality of the generated meshes can be satisfied with the requirements of finite element numerical simulation.

two-dimensional domain;all-quadrilateral mesh;triangle merging;graded mesh;numerical simulation

TK 124;TP 391.41

A

10.3969/j.issn.1673-5005.2011.02.023

2010-04-20

国家自然科学基金项目(50904077);中央高校基本科研业务费专项资金资助项目(10CX05011A)

修荣荣(1977-),女(汉族),山东莱阳人,硕士,主要从事CDF/NHT技术研究。

1673-5005(2011)02-0131-06