讲授大学化学中热力学第二定律的探讨

彭庆蓉 高海翔 张春荣 王红梅 刘霞 鲁润华

(中国农业大学理学院应化系 北京 100083)

由于大学化学教材中不直接提出热力学第二定律，而是将热力学第二定律隐含在化学反应的自发性和化学平衡中，使得大部分学生很难系统地掌握这部分内容。作者在教学实践中发现，热力学第二定律与熵概念是教学的重点和难点[1-5]。所谓化学反应的自发性实际上就是化学反应的方向，而化学平衡指的是化学反应的限度。化学反应的方向和限度就是热力学第二定律要解决的问题。从热力学第二定律的提出背景[6-8]、热力学第二定律的表述[9]以及热力学第二定律的数学表达式等几个方面进行讲授，并注意强调这几部分内容之间的内在联系，可以收到良好的教学效果。对于如何作好此环节的教学，本文提出如下建议。

1 热力学第二定律的提出背景

在热力学发展史上，热力学第二定律的建立是与热机效率相联系的。热力学定律的发现是工业革命与技术革命的必然结果。蒸汽机的发明与不断改进促进了第一次工业革命，但当时的效率是很低的，能量浪费很大。因而，制造能源利用效率高的机器成为人们研究的课题。在研究此类问题时，人们发现，要制造效率高于100%的热机(第一类永动机)是不可能的。这一发现直接导致了能量守恒定律，即热力学第一定律的建立。在此基础上，人们又提出了一个问题，即能否实现效率为100%的热机? 热力学第一定律指出，各种形式的能量在相互转化的过程中必然满足能量守恒，违反能量守恒的过程不可能发生，但是否能够推断出只要在理论上满足能量守恒的热力学过程都能够实现呢?

下面看两个例子，在25℃和101.3kPa下，1mol H2和0.5mol O2生成1mol液态水，每进行1mol这个反应，就有286kJ热量放出，如果用286kJ的热量加热1mol水，在25℃和101.3kPa下，只能看到水的气化，不可能变成H2和O2；要使这个反应从右向左进行，必须加电压进行电解。也就是说这个反应在25℃和101.3kPa下有一定的方向，只能从左向右进行。第2个例子，H+和OH-几乎在混合的同时就发生反应，H+和OH-极易结合生成水分子，但最后剩下少量H+和OH-不反应([H+][OH-] = 10-14mol2.dm-6达到平衡)，这说明酸碱中和反应具有一定的限度。再比如，热力学第一定律告诉人们自然界能量总值恒定，那么能量就不可能减少，为什么还会有能源危机呢？热力学第一定律回答不了这个问题。其实能量并没有变少，只是在转化时保持总值不改变的前提下，从一种形式变成另一种形式是有方向性的，不能随意改变。

总之，上面提出的这些问题是方向和限度问题，是热力学第一定律回答不了也解决不了的问题。热力学的任务第一是系统与环境的能量转化，这是热力学第一定律讨论的内容。热力学的其他任务是化学反应以及物理过程的方向与限度。热力学第一定律只解决了能量守恒，它回答不了热力学中的其他问题。自然界过程的方向和限度如何？这是热力学第二定律要解决的问题。自然界的过程除了遵守能量守恒定律之外都有一个固定的方向，违反这个方向就不可能发生。所以热力学第二定律与热力学第一定律一样，是一个与能量有关的普遍规律，是人们长期实践经验的总结，不需要严格的数学证明。下边来看看人们是如何发现自然界过程的方向的。

先谈方向，通常所说的一个过程的方向指的是自发过程的方向。自发过程(spontaneous process)是在一定环境条件下，没有外力作用，系统自动发生或完成的过程。反之，只有在外力作用时才能发生的过程为非自发过程。通常所说的“过程方向”指自发过程的方向，不是说另外一个方向的过程绝对完成不了。比如，水自发流动的方向是从高处流向低处，并不是说水不能从低处流向高处，如果给它施加外力，比如说用水泵，就可以把水从低处引向高处，这一过程就是非自发过程。通常说水流方向指的是自发过程的方向。下面所说的方向都是自发过程的方向。

再来看下面4个例子：(1) 气流流动的方向是从高压流向低压，限度是两边压力相等即力学平衡；其逆过程气流从低压流向高压必须要压缩机，所以这个过程是非自发过程。(2) 热量传递的方向是从高温物体传到低温物体，限度是两边温度相等即热平衡；其逆过程热量从低温传向高温是非自发过程。比如冰箱，把箱体低温的热量放到外面空气中，如果没有制冷机，没有电，热量从低温传到高温是不可能的。(3) 一杯糖水，左边是浓糖水，右边是稀糖水，水会从含水量高的一侧扩散到含水量低的一侧，糖从含糖量高的一侧向含糖量低的一侧扩散，限度是两边糖的浓度相等即相平衡；这一过程的逆过程也是非自发过程。(4) 化学反应中的酸碱中和反应生成盐和水，这个反应是自动发生的，这就是反应的方向，由左向右，限度是化学平衡(前面谈到的[H+][OH-]=10-14mol2·dm-6达到平衡)；这一反应的逆反应同样是非自发过程，可以通过电解食盐水来完成这一非自发过程。

2 自发过程的共同特点

综上所述，自发过程的共同特征之一是自发过程都是单向地朝着平衡，前面4个例子中的平衡分别是力学平衡，热平衡，相平衡以及化学平衡。第2是自发过程都有做功本领。做不做功要看有没有合适的装置，有了合适的装置就能做功。气流从高压传向低压只要在中间加一个气压机就可以做功；热从高温传到低温之间放置一个热机，就可以做功；物质从高浓度向低浓度扩散具有做功本领，扩散电池或者浓差电池就是利用物质扩散做功这一原理做成；酸碱中和反应具有做功本领，它可以一边中和，一边放电。总之自发过程都具有做功本领。第3个特点是自发过程都是不可逆的。上面所举的例子，既有物质传递，也有能量传递，表面上看，这些例子并不相关，实际上都涉及到功与热的相互转换。

人们在长期实践中总结发现自然界的任何一个具体过程都与功和热的相互转换有关。因此，最根本的问题是功与热的相互转换。功变热和热变功这两个过程是不等价的。前面所举的例子本质上都能回到功与热的问题上。功可以无代价地全部变为热；反过来，热不可能无代价地全部变为功。这就是前面那些例子反映的共性，即功热相互转化不等价。功可以无代价地全部变为热，譬如两手相合摩擦生热，功完全变成热；而热不可能无代价地全部变为功，譬如公路上跑的汽车，引擎发热一部分用于做功使得汽车运动起来，另一部分热会散发到空气中。热不可能全部变成功还有一个明显的例子就是小球的自由落体运动，小球第二次弹起的高度比第一次低，以后每一次弹起的高度都比前一次低，最后小球停止下来。这是由于小球每一次与地面发生碰撞都有部分热量传给地面而损失，另外一部分热量传给小球变成功，所以小球每一次弹起的高度都不如前一次高。假如小球的能量没有损失，那么它每次弹起的高度都会与第一次相同；果真如此的话，小球就会永不停止地一直运动下去，事实上这是不可能的。所以功与热相互转化是不等价的，这是人们长期实践总结出来的经验。这就是共性，把那些看来不相干的事归结到功热相互转换从而统一起来，也就是热力学第二定律很多种表述中的一种。

3 热力学第二定律的文字表述

在科学史上，热力学第二定律具有多种不同的表述形式，其中最具有代表性的是开尔文和Clausius表述。开尔文表述为“不可能从单一热源取热使之完全变为功而不产生其他影响”；Clausius表述为“不可能把热量从低温物体传到高温物体而不引起其他变化”。这看似不同的表示形式，却揭示了热力学过程共同的本质特性：自然界的一切实际过程都是不可逆的或者说一切自发过程都是有方向性的。Clausius表述反映了热传递这一具体的自发热力学过程的不可逆性或方向性；开尔文表述则揭示了热功转化这一具体的自发过程的不可逆性或方向性。因此，任何不可逆的热力学过程，都可以作为热力学第二定律的表述形式。各种具体的表述形式之间，其一致性都是可以得到证明的。热力学第二定律的发现是一个由特殊到普遍，再由普遍到特殊的认识过程。至此,学生也就能够明白热力学第二定律所揭示的本质，同时也使学生能深刻体会自然现象、历史都是不可逆的，客观规律是不能违背的，要珍惜光阴，珍惜人生。

4 热力学第二定律的数学描述

4.1 熵函数的引入

热力学第二定律可以用于判断过程的方向和限度，但这个结论一般很难运用，于是人们希望把这个结论变成一个数学表达式，就像热力学第一定律一样用一个数学公式表达出来。为了把热力学第二定律用数学公式表达出来，Clausius在1850年作出热力学第二定律的表述之后，在1865年又引进了一个状态函数——熵(entropy)，并把它作为判断过程方向的共同判据。如果在此时直接给出熵的定义，然后从混乱度的角度解释熵函数以说明过程的方向似乎是比较具体的(大学化学教材正是如此)，但却把自发过程的共同特征与过程方向的共同判据割裂开了，然后又把混乱度与过程的方向联系起来，这样做不仅反映不出热力学第二定律建立过程的本质，而且会导致越讲越乱。作者在教学中发现，如果继续推理前面提到的思路，按Clausius的思路继续推导，对学生的逻辑推理能力应该会有帮助[10-11]。

在授课中，可先讲卡诺循环(对于农林院校的本科生，这部分推导可以省略，提示有兴趣的学生可以自学)。 热力学第二定律指出，热机的热效率不可能达到100%。那么，在一定条件下，热机的热效率最大能达到多少？热机是通过某种工作介质，将热转换为功的装置。在两个热源之间工作的热机效率，即：

法国工程师卡诺在深入考察了蒸汽机工作的基础上，于1824年提出了一种理想的热机工作循环——卡诺循环。卡诺假设一热机中有一定量的工作介质，工作在温度分别为T1和T2的两恒温热源间。卡诺循环由两个可逆的定温过程和两个可逆的绝热过程(定熵)组成，所有工作于同温热源与同温冷源之间的热机，其效率都不能超过可逆机 (换言之，即可逆机的效率最大)，这就是卡诺定理(可用热力学第二定律加以证明，在这里不作介绍)。由卡诺定理可推出：所有工作于同样温度的一对热源之间的可逆热机，其效率与卡诺机相同，而与其工作介质无关；而不可逆热机的效率必小于卡诺机。即：ηir<ηr=ηcar。对工作在两个热源之间的可逆热机变换为:

也就是说,可逆热机的热温商之和等于0，任何不可逆热机的热温商之和小于0，这就是Clausius不等式：

对于一个任意的循环过程来说，Clausius不等式的形式是：

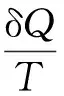
在熵概念的教学中，要注意知识的连贯性。把熵的概念和热力学第二定律所反映的实质联系起来。热力学第二定律告诉人们，自然界一切宏观过程是不可逆的，其自发进行是有方向的。熵增加原理接着告诉人们进行的方向，孤立系统总是朝着熵增加的方向进行。在教学过程中，要注意强调熵的状态性和广延性，注意它的绝对性和相对性。

4.2 热力学第二定律的数学表达式

Clausius在熵函数定义基础上得出这样一个结论：在不可逆过程中,系统的熵变大于过程的热温商;在可逆过程中,系统的熵变等于过程的热温商。即系统中不可能发生熵变小于热温商的过程，这是一切非敞开系统的普遍规律。这就是热力学第二定律，其数学表达式为：

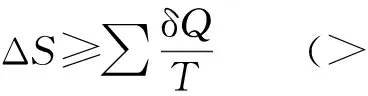
式中T是环境温度：当使用其中的“=”时，可认为T是系统温度。

这样安排教学顺序，符合科学发展的规律。环环相扣，不仅有利于学生理解，而且可以激发学生的学习兴趣，调动学生学习的积极性。同时也能提高学生的逻辑推理能力，使之能较好地掌握熵函数的实质。

一个体系能否发生一个指定的过程而达到某一终态，就可以用上式来判断。对于绝热体系或隔离体系来说，用上式判断方向和平衡非常方便；因为在此两个体系中，Q=0，故有ΔS>0，只要看熵函数的变化是否为0即可判断过程的方向性。但一般过程Q不一定为0，ΔS的值就必须与实际过程的热温商(Q/T)相比较才能得出结论，很不方便。那么，对于一个等温等容过程或等温等压过程，如何判断它达到终态的可能性呢?对此，可通过进一步的演绎推理，从而得出几个新的状态函数来解决。

4.3 把特殊条件下热力学第二定律的表达式纳入教学内容

传统的热力学第二定律的两种表述可认为是一般的普遍表述，但由于表述的多样性，还可结合实际问题和条件，将定律的表述作适当延伸，典型的有等温等容和等温等压。例如在等温条件下，将热力学第二定律数学表达式做如下变形：

(T2S2-T1S1)-(U2-U1+W)≥0,(U2-T2S2)-(U1-T1S1)≤-W

此时定义A=U-TS为亥姆霍兹自由能，这样热力学第二定律数学表达式就变为：ΔA≤-W。对于等温等容过程，系统对外做功W=0，也就是ΔA≤0，这就是等温等容条件下，热力学第二定律的亥姆霍兹自由能表达式，它的物理意义是：在等温等容过程中，系统的自由能永不增加，即在等温等容条件下，系统中发生的一切不可逆过程，总是朝着自由能减少的方向进行，到达热平衡时，自由能最小。同理，还可推出在等温等压条件下，热力学第二定律的吉布斯自由能表达式ΔG≤0，它的物理意义是：在等温等压条件下，吉布斯函数永不增加，即在等温等压条件下，系统中不可逆过程总是朝着吉布斯函数减少的方向进行，到达热平衡时，吉布斯自由能最小。

至此，人们从长期实践经验总结的“不可能从单一热源取热使之完全变为功而不产生其他影响”或“不可能把热从低温物体传到高温物体而不产生其他影响”这一自然界的基本原理出发，经过想象、分析、综合、演绎等推理过程，得出了关于过程进行方向和限度的判据——S、A、G。这些推理过程符合科学的发展过程，而经过这些合理推理所得出的结论与实际现象相吻合。故讲好这些过程，无疑会对学生以后的学习和工作能力的培养具有相当的重要性。

[1] 邹邦银.高等函授学报(自然科学版),1997,2:23

[2] 蒋爱华,艾元方,蒋绍坚.理工高教研究,2005,24(2):51

[3] 施云海,彭阳峰,程亮,等.化工高等教育,2007,5:70

[4] 宋金瑶,闫荣义.南阳师范学院学报(自然科学版),2003,2(6):109

[5] 崔瑜瑾.长治学院学报,2009,26(2):80

[6] 汪达开.南京师范大学学报(自然科学版),1996,19(4):81

[7] 高炳坤.大学物理,1999,18(12):17

[8] 胡珍珠,朱志昂.高等理科教育,2001,35:75

[9] 曹良腾,罗来辉.物理教学探讨,2008,26(315):43

[10] 邵理堂.山东科技大学学报(自然科学版),2001,20(2):26

[11] 刘烈昌.赣南师范学院学报,2004,6:113