应用Turbo乘积码的改进UWB判决反馈ATR接收机
杨 刚1,亢 洁
(1.西安邮电学院 通信与信息工程学院, 西安 710061;2.陕西科技大学 电气与信息工程学院,西安 710021)
1 引 言
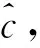

图1 一般数据辅助ATR接收机的结构Fig.1 Structure of DA-ATR receiver
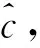
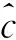
2 Turbo乘积码
Turbo乘积码(TPC)是将Turbo码迭代译码的思想应用于二维乘积码中所形成的新型Turbo码[4]。如果将乘积码水平方向的编码看成是第一个子编码器、垂直方向的编码看成是第二个子编码器、两次编码读出的顺序等效为一个方阵均匀交织器的话,那么二维乘积码实质上可以看作是中间插入了行列交织器的分组码的串行级联,如图2所示。通常,可选择相同的分组码作为子码,形成参数为(n2,k2,d2)的乘积码。常见的作为TPC子码的分组码,包括扩展汉明码和扩展BCH,其中扩展汉明码是在汉明码的基础上增加一个全校验位得到的。由于它编译码非常简单,很容易实现,对突发错误具有较强的纠错能力,且码长是8的整数倍,特别适合微处理器进行数据处理,从而得到了广泛的应用。
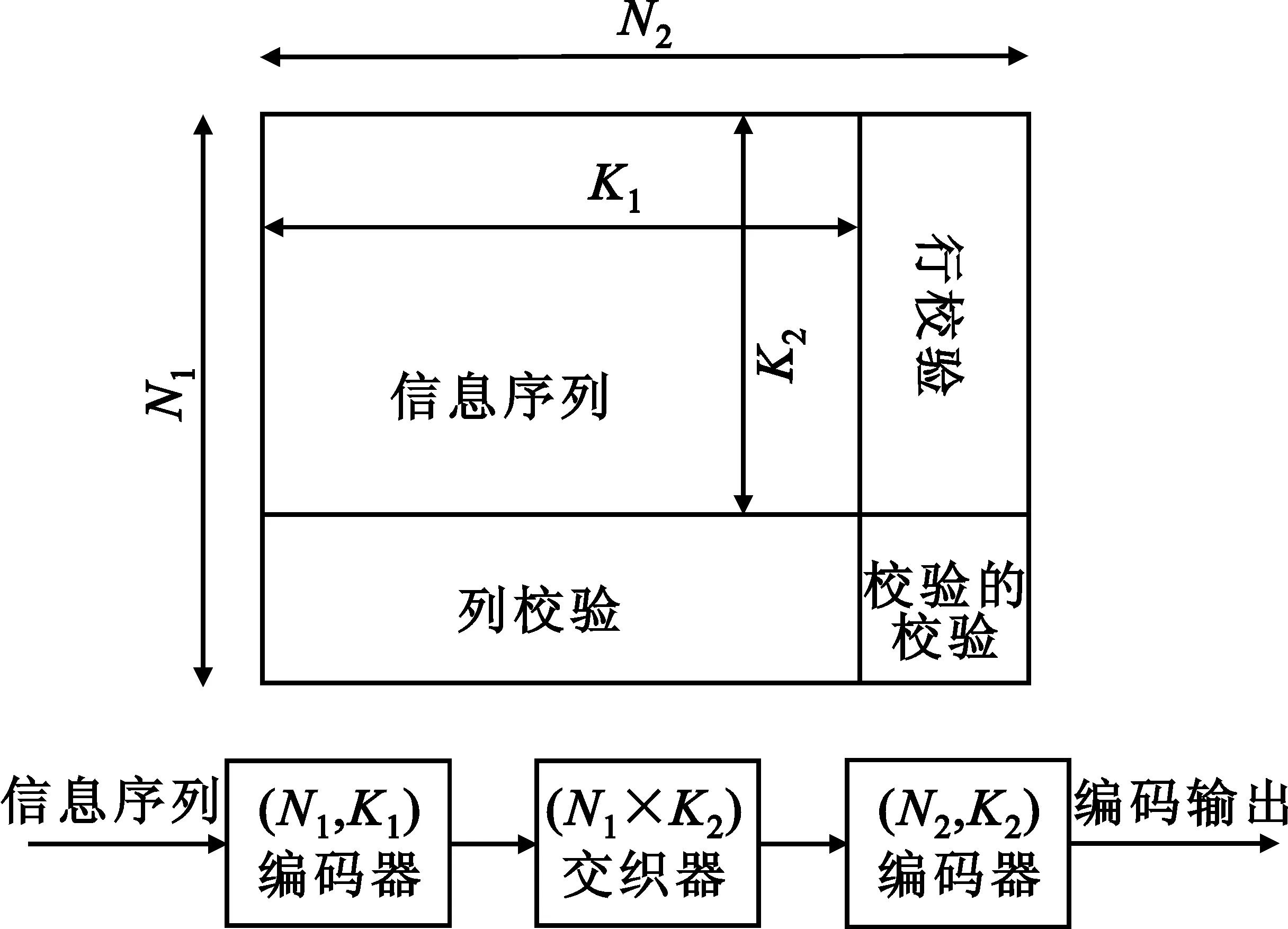
图2 二维乘积码的编码结构Fig.2 Encoding structure of two-dimension product code
由于TPC使用简单的行/列交织器就能获得近似于Turbo卷积码(TCC)中随机交织器的码的最小距离性能,因此明显减小了编码复杂度。TPC的译码可以分解为多次行码和列码的单独译码,这样一个译码单元即可完成多次迭代,大大减小了实现电路的复杂度和译码时延,同时其译码复杂性随行码和列码译码复杂性仅为线性增长关系。在实践中,TPC译码算法一般采用修正的Chase迭代译码算法[5],不仅性能接近最优的MAP算法,而且具有复杂性较小、对译码过程中的有限字长效应不敏感、无需估计信道的噪声方差等优点。另外,TPC可以纠正信道的突发错误,特别适合在信道条件较差的无线通信中使用,而且不像TCC,几乎不存在误码平层效应。在高码率,甚至接近信道容量时,TPC仍具有较强的纠错能力。相比于TCC,TPC的译码时延大大减小,具有较好的实时性。鉴于TPC的出色性能和简单结构,目前AHA等公司已推出了商业化的Turbo乘积码的编译码器[6],在IEEE 802.16工作组的宽带无线接入系统标准中,TPC被推荐为该系统的前向纠错码[7]。
基于以上因素,本文在相关器输出判决后加入了应用Turbo乘积码进行反馈判决量纠错的机制,形成一种改进的UWB接收机,称为TPC码判决反馈的DA-ATR接收机(以下简记为TPC-DA-ATR)。后面的性能仿真中,在TPC码的参数选择时,行码和列码均选取扩展汉明码(16,11,4)作为子码,形成的二维乘积码参数为(256,121,16),TPC译码算法采用修正的Chase迭代译码算法,译码迭代4次。
3 改进TPC-DA-ATR接收机的结构和性能分析
这种改进的TPC-DA-ATR接收机的具体结构组成如图3所示。假定每个接收的比特数据符号由Ns个UWB脉冲信号的接收波形所组成,脉冲的间隔为Tp,比特数据间隔Td=NsTp,延时D等于译码延时与Td之和。当然,由于TPC译码器存在一定的译码延时,相应的数据信号波形的延时将会有所增加,等于译码延时与数据间隔Td之和。

图3 改进TPC-DA-ATR接收机的结构Fig.3 Structure of improved TPC-DA-ATR receiver
同一般ATR接收机一样,每一帧在开始阶段将首先发送参考脉冲,其个数为N0,随后发送Nd个比特数据信号。N0个参考脉冲接收信号经累加平均后得出起始模板信号rm0为
(1)
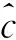

(2)
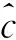
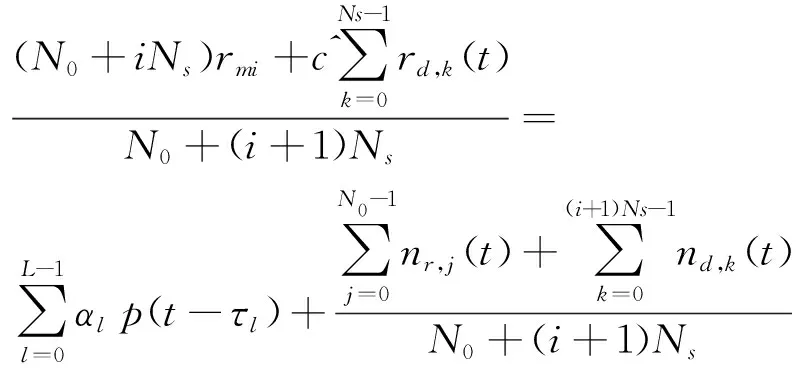
(3)
式中,1≤i≤Nd,Nd为发送的比特数据总数,必须小于信道保持时不变的最大比特数Nmax(如IEEE 802.15.3a中建议的8 192 bit)。这样,当i足够大时,式(3)相当于对N0+(i+1)Ns个参考信号取平均,第二项噪声将趋近于零,所形成的模板信号将趋近于理想的干净模板信号。这时,TPC-DA-ATR接收机可以达到接近于最优的误码率性能,同时传输效率非常接近于1。
4 多径信道下的性能仿真和结论
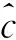
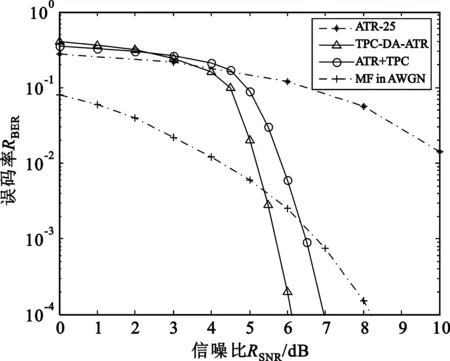
图4 CM3信道下改进TPC-DA-ATR接收机的性能Fig.4 Performance of improved TPC-DA-ATR receiver under CM3 multipath channel
从图中可以看出,在低信噪比区域,TPC-DA-ATR接收机和ATR+TPC接收机的性能相差不大。随着信噪比的逐渐增加,错误判决数量逐渐下降,TPC-DA-ATR可以结合更多数量的正确判决信号来平均得出模板信号,性能很快得以改善,而ATR+TPC性能改善较慢,导致TPC-DA-ATR在信噪比大于2.3 dB小于4.5 dB时稍优于ATR+TPC,但此时的性能差距并不大。
在信噪比大于4.5 dB的区域,TPC-DA-ATR和ATR+TPC的性能曲线均呈现瀑布状,误码率都远远优于未编码的ATR-25接收机,在10-4比特误码率时,甚至都超过了AWGN噪声下理想的未编码的匹配滤波器接收机。这主要是由于TPC码的强纠错能力起了作用,所带来的性能提高已远大于TPC编码的传输效率下降所带来的性能降低所致。同时,TPC-DA-ATR仍优于ATR+TPC,且性能优势变得比较明显。究其原因,是由于此时的错误判决很少,TPC-DA-ATR的模板信号经反馈更新由更多数量的信号平均得出,更为干净,而ATR+TPC的模板信号仍为25个参考信号平均得出,含噪较多,导致两者之间的性能差距变大。当信噪比等于6 dB时,误码率分别为2×10-4和6×10-3,相差一个数量级。如果以10-4比特误码率作为基准,TPC-DA-ATR优于ATR+TPC约1 dB增益。
仿真结果表明了本文提出的加入Turbo乘积码的译码器,将其输出作为更新模板时的判决量,以降低错误判决传播的改进思路是可行的,比单纯ATR+TPC纠错的UWB接收机的检测性能有优势;加之其结构较简单,TPC码的译码复杂度仍属中等水平,还具有实际应用的潜力。
参考文献:
[1] Choi J D, Stark W E. Performance of Ultra-Wideband Communications With Suboptimal Receivers in Multipath Channels[J]. IEEE Journal on Selected Areas in Communications, 2002,20(9):1754-1766.
[2] Franz S, Mitra U. On optimal data detection for UWB transmitted reference system[C]//Proceedings of 2003 IEEE Global Telecommunications Conference. Francisco, USA: IEEE,2003:744-748.
[3] Zhao S, Liu H, Tian Z. A decision-feedback autocorrelation receiver for pulsed Ultra-Wideband systems[C]// Proceedings of 2004 IEEE Radio and Wireless Conference. Atlanta: IEEE,2004:251-254.
[4] Pyndiah R. Near-optimum decoding of product codes: block Turbo codes[J].IEEE Transactions on Communications,1998, 46(8):1003-1010.
[5] Hirst S, Honary B, Markarian G. Fast Chase algorithm with an application in Turbo decoding[J]. IEEE Transactions on Communications,2001, 49(10): 1693-1699.
[6] Cecilia E, Sandoval R. Modular Programming of functions for turbo product codes on FPGA[J]. Revista Tecnica De La Facultad De Ingenieria Universidad Del Zulia,2008, 31 (3): 294-301.
[7] Williams D, Sonander S. Turbo product code forward error correction: capability and benefit[R].[S.l.]:IEEE 802.16 Broadband Wireless Access Working Group, 2000.
[8] Foerster J.Channel Modeling Sub-committee Report Final[R].[S.l.]:IEEE P802.15 Wireless Personal Area Networks Working Group, 2003.

