等温大气压高方程在气压剖面高度计算中的应用
董 涛,李永军
(国家海洋技术中心,天津 300112)
等温大气压高方程在气压剖面高度计算中的应用
董 涛,李永军
(国家海洋技术中心,天津 300112)
气象探测仪器获取空中气象数据时,需要确定气象数据对应的气压高度,以形成剖面测量数据。将等温大气压高方程应用于实际的气压剖面高度计算中,确定计算的边界条件并进行误差估算,并通过实际算例,验证了理论计算的有效性。
等温大气压高方程;气压高度;误差估算
在空中气象探测仪器获取空中气压、温度、湿度和风速等数据时,需要确定气象测量值对应的气压高度。本文把等温大气压高方程应用于实际的气压高度计算中,对方程作某些特定假设,忽略重力加速度的变化和水汽影响,并对由此可能带来的计算误差进行估算,建立了实际应用基础。采用中国气象科学数据共享服务网的高空探测数据[1]进行计算分析,计算结果验证了理论计算的有效性。
1 理论计算方法
1.1 基本原理
剖面高度计算的基本原理是基于大气静力学方程[2]。假设大气相对于地面处于静止状态,则某一点的气压值等于该点单位面积上所承受铅直气柱的重量,如图1。

图1 空气静力平衡图
在大气柱中截取1单位面积厚度为△Z的薄气柱。设高度Z1处的气压为 P1,高度Z2处的气压为P2,空气密度为ρ,重力加速度为g。在静力平衡条件下,Z1面上的气压P1和Z2面上的气压P2间的气压差应等于这两个高度面间的薄气柱重量,即:

式中:P1为高度Z1处的气压值;P2为高度Z2处的气压值;ρ为空气密度;g为重力加速度;△Z为Z2与Z1之间的高度差。
(1)式中负号表示随高度增高,气压降低。若△Z趋于无限小,则(1)式可写成:

由(2)式可以看出,气压随高度递减的快慢取决于空气密度和重力加速度的变化。重力加速度随高度的变化量一般很小,因而气压随高度递减的快慢主要决定于空气的密度。在密度大的气层里,气压随高度递减得快,反之则递减得慢。实践证明,静力学方程虽是静止大气的理论方程,但除在有强烈对流运动的局部地区外,其误差仅有1%,因而得到广泛应用。飞机给出的绝对高度(海平面气压高度)也是根据这个原理计算的。
1.2 压高方程
为了精确地获得气压与高度的对应关系,通常将静力学方程从气层底部到顶部进行积分,即得出压高方程[3]:
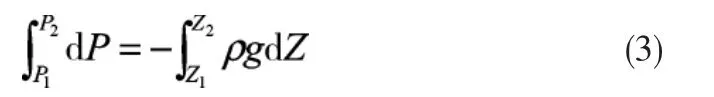
式中:Z1为第1点高度值;Z2为第2点高度值;P1为Z1点高度的气压值;P2为Z2点高度的气压值。该式表示任意两个高度上的气压差等于这两个高度间单位截面积空气柱的重量。
理想气体状态方程[3]见(4)式:

式中:P为气压;ρ为气体密度;R为比气体常数;T为绝对温度。
将(3)式和(4)式联立,可以得到:

(5)式是通用的压高方程,表示气压随高度的增加而按指数规律递减。而且在大气低层,气压递减得快,在高层递减得慢。在温度低时,气压递减得快,在温度高时,递减得慢。
1.3 计算分析
1.3.1 等温大气压高方程
利用压高方程,原则上可以进行气压和高度间的换算,但直接计算还比较困难。因为在公式中指数上的子式中,g和T都随高度变化,而且R因不同高度上空气组成的差异也会随高度而变化,因而进行积分是困难的。为了方便实际应用,需要对方程作某些特定假设。比如忽略重力加速度的变化(在100 km以下的低层大气g随高度的变化很小,可以忽略)和水汽影响,并假定气温不随高度发生变化,此条件下的压高方程,称为等温大气压高方程。在等温大气中,上式中的T可视为常数。
则(5)式可以写成:

将绝对温度T换成摄氏温度t,自然对数换成常用对数,并将g和R代入,则(6)式就可以写成气象上常用的等温大气压高方程:
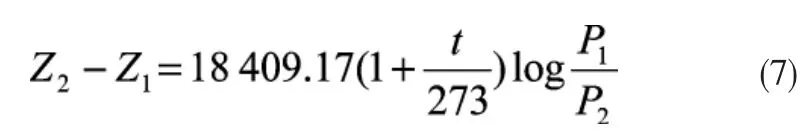
式中:t为气体温度(℃)。
1.3.2 计算初值的选择
在空中测量完成后,根据测量得到的温度及气压值,计算气压高度。从最后一组测量数据开始计算,假定每两组测量数据之间的薄层温度不变,则可使用公式(7),计算其高度差,把各个薄层的高度差相加即为待求的气压高度。
计算初值选择应选择最后一组有效气压温度值。
2 误差分析
2.1 忽略重力加速度的变化带来的误差
2.1.1 重力加速度g随高度的变化。
在地球的高空,一般不考虑地球的自转,这时物体所承受的万有引力就是重力。
重力加速度可以用下式表达:

式中:R是地球半径;h是高度。
实际应用中,高度h一般不超过15 km,而地球平均半径R是6 371.004 km,h<<R,可以忽略高度变化对重力加速度的影响。
2.1.2 纬度变化对重力加速度的影响
根据“1967年国际重力公式”:

式中:φ为测量时所处的纬度值。表1是不同纬度重力加速度对剖面高度计算的影响。
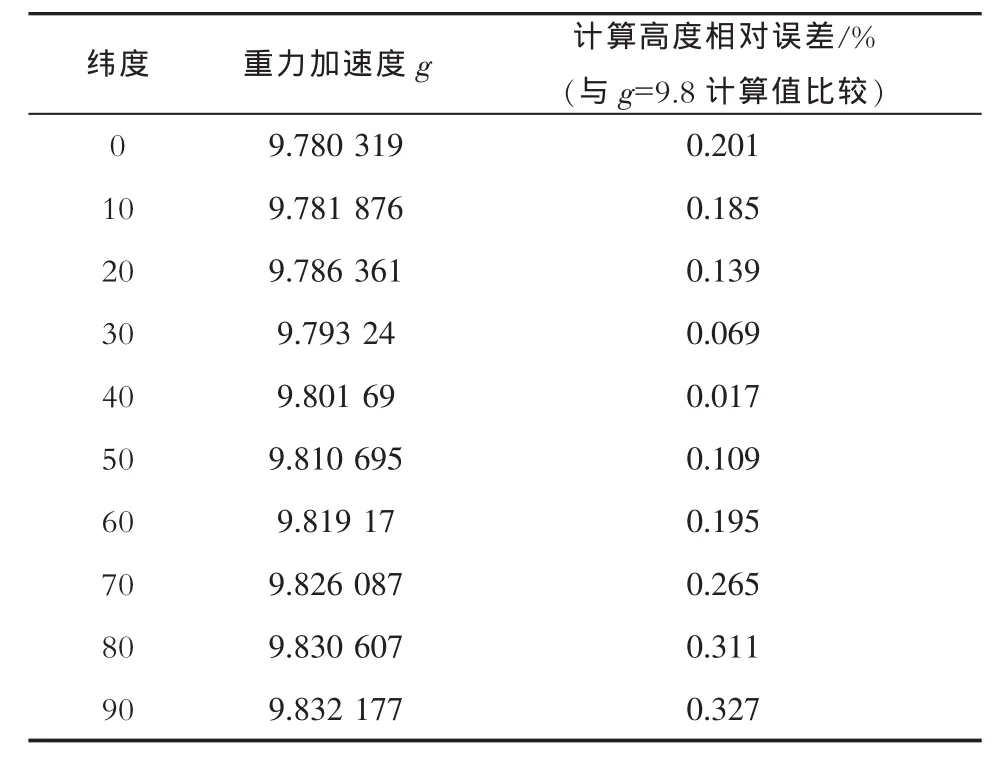
表1 不同纬度重力加速度的影响
由表1可以估算出,即使在两极计算气压高度,重力加速度使用g=9.8,在计算高度达到3 000 m时,计算绝对误差为9.81 m,相对误差仅为0.327%,因此,重力加速度可以使用g=9.8,而忽略由于纬度不同带来的计算误差。
2.2 实际空气假设为干空气引起的误差
压高计算公式把实际空气当成干空气处理,但当空气中水汽含量较高时,可以用虚温TV代替实际温度T:
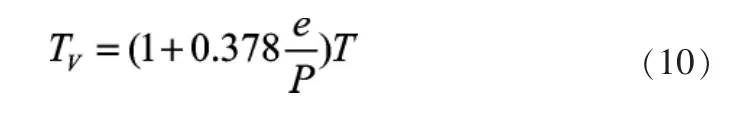
式中:TV为气体虚温;e为湿空气的水汽压;P为气压;T为气体绝对温度。
定义KT为虚温的影响因子:

那么(7)式可改写为:

实际应用中,湿空气的水汽压e较难得到,因此,需要把湿空气假设为干空气,下面估算由此带来的误差。
当空气湿度达到最大,即100%时,湿空气的水汽压等于该状态下的饱和水汽压,此时,对计算的影响最大。表2给出了不同温度下的影响因子KT。
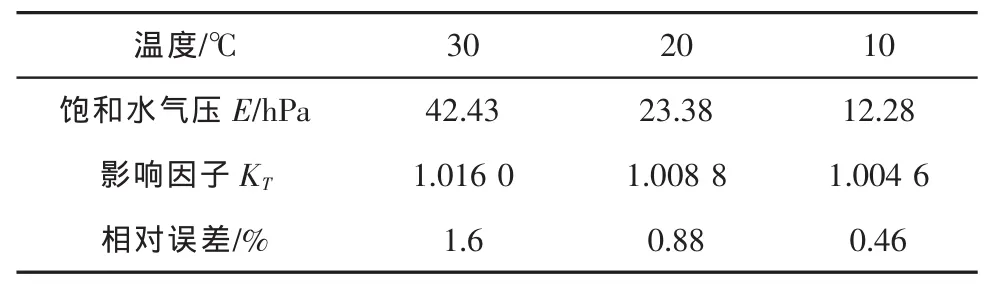
表2 不同温度下的影响因子KT
需要指出的是,上述影响因子是在相对湿度为100%时计算得出的,而且湿度随高度按指数规律迅速衰减,在3 000 m高空,湿度仅为地面的25%,因此,在相对湿度未达到100%,高度0~3 000 m的范围内,影响非常小,影响因子接近1,因此可以忽略把湿空气处理为干空气带来的误差。
3 算例分析
3.1 算例资料
算例资料来源于中国气象科学数据共享服务网的高空探测数据,数据时间为2008年6月6日0点与12点,台站选择北京站(39.80°N,116.47°E)与香港站(22.32°N,114.17°E)。计算初值选择气压1 000 hPa时测量得到的高度和温度值,此时的测量高度值为计算的初始高度。
3.2 算例计算结果
计算结果分别见表3~表6。

表3 气压高度测量值与计算值比较(2008-06-06 0点北京高空探测数据)

表4 气压高度测量值与计算值比较(2008-06-06 12点北京高空探测数据)
3.3 算例计算结果分析
(1)气压高度计算值的最大相对误差在1%左右;在3 000 m高空左右,最大相对误差0.877%。
(2)由于高空探测数据较粗糙,测层高度差较大,无法准确给出测层温度,计算中,把两个测量点的温度平均值做为测层温度,导致计算误差相对较大,可以预计,如果测层密集,气压高度的计算值与测量值的误差将大大降低。
(3)气压高度的计算值,绝对误差会随着高度的增加而增加,但相对误差随高度的增加而减小。
通过算例,验证了理论计算的有效性,说明该方法可以应用到实际的空中剖面高度计算中。

表5 气压高度测量值与计算值比较(2008-06-06 0点香港高空探测数据)

表6 气压高度测量值与计算值比较(2008-06-06 12点香港高空探测数据)
[1]中国气象科学数据共享服务网,高空探测数据.
[2]黄荣辉.大气科学概论[M].北京:气象出版社,2005:19-21.
[3]李爱贞,刘厚凤.气象学与气候学基础[M].北京:气象出版社,2004:25-27,103-106,79-81.
Abstract:Air pressure height should be obtained when weather instrument is detecting weather datum in order to acquire profile datum.The isothermal atmosphere air pressure-height equation is applied on the air pressure-height calculation.Boundary condition and error estimate are provided.The validity of the theory is proved by examples.
Key words:isothermal atmosphere air pressure-height equation;air pressure height;error estimate
The Application of Isothermal Atmosphere Air Pressure-height Equation on Air Pressure Profile Height Calculation
DONG Tao,LI Yong-jun
(National Ocean Technology Center,Tianjin 300112,China)
P43
A
1003-2029(2011)01-0088-04
2009-12-28

