三角模糊变量规划问题的研究

成亚丽

(成都电子机械高等专科学校 信息与计算科学系，成都 610071)

三角模糊变量规划问题的研究

成亚丽

(成都电子机械高等专科学校 信息与计算科学系，成都 610071)

针对含模糊变量的线性规划问题，研究其求解方法。通过比较优于面积的大小来确定三角模糊数的序关系，将此方法应用于模糊线性规划问题中，通过实例证明此方法是有效的。

三角模糊数;模糊变量;模糊线性规划;排序;优于度

数学规划问题是个古老的课题，长期以来人们对它进行了深入地探讨和研究，但一直没有形成独立的、系统的学科。1965年，美国加利福尼亚大学专家L.A.Zadeth教授［1］提出了模糊数集理论。20世纪70年代初，Tanaka教授和Zimmermann教授［2］提出了模糊线性规划问题。从求解方法来看，模糊线性规划分为模糊约束关系型线性规划和模糊系数型线性规划［3］。这些问题变量本身是分明的，然而在工程问题中，常常遇到求最优解是多少或者比较优越的解是多少，这时的变量应为模糊变量，相应的规划问题就成为变量为模糊数的线性规划问题。笔者针对模糊数中最常见的三角模糊数，基于其线性特点，提出一种三角模糊数的新排序方法，利用新定义的模糊序关系，将它转换成一个多目标线性规划问题，从而简化问题的求解。

1 模型的建立

定义 模糊线性规划问题如下［4］:

其中A=(aij)m×n为m×n阶矩阵;c=(cj)1×n为n维清晰行向量为m维模糊数列向量为n维模糊变量)为清晰系数为模糊常数)为模糊变量。另)为三角形模糊数(如图1所示)。其中

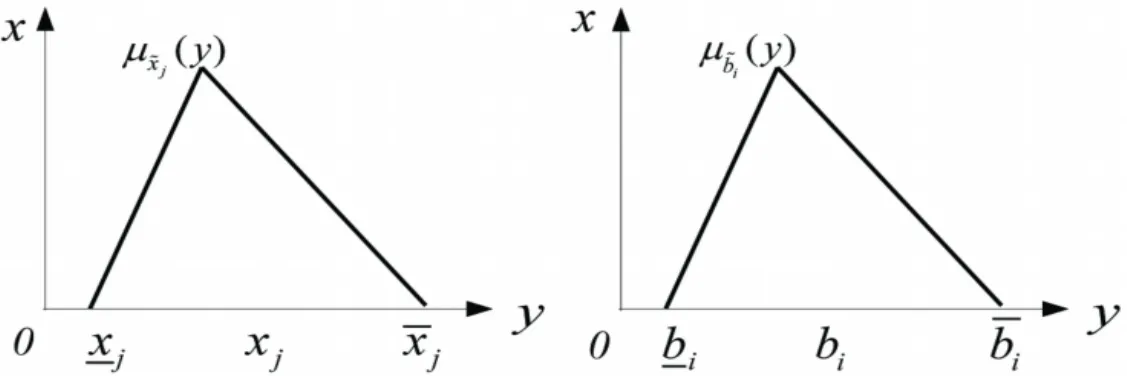
图1和的图示

2 三角模糊数的排序

定义1［5］实数域R上的模糊集称为一个模糊数，若满足:

a.存在x0∈R，使

R上的全体模糊数记为F(R).

3 给予优先关系的三角模糊数排序

定义2［6］设为2个三角模糊数，如果对于任意的，则称。

在大部分情况下，AL(λ)〉BL(λ)，AR(λ)〉BR(λ)(∀λ∈［0，1］)并不同时都成立。因此，根据三角模糊数的特点，对三角模糊数˜A、˜B的左、右边分别进行比较，然后再综合。于是，在λ截集下，考虑左边的情形，令:

图2

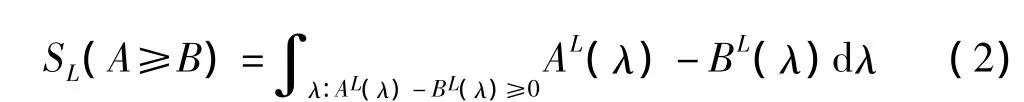
考虑右边的情形，令:

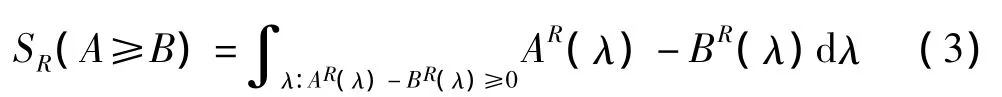
同理:

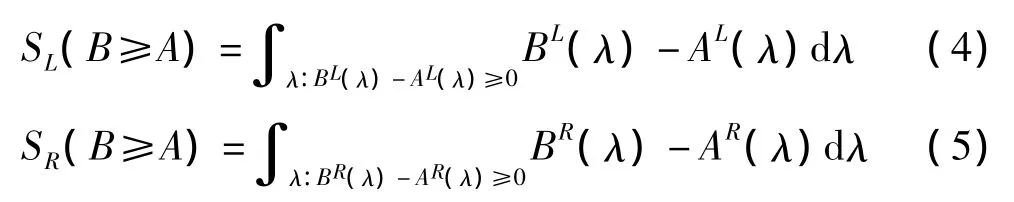
根据三角模糊数的特点，可以写成如下形式:

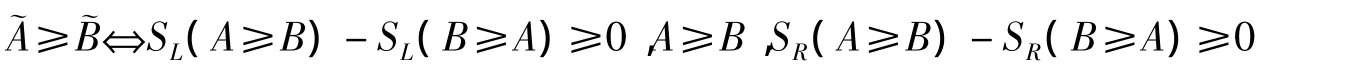
其中，SL(A≥B)-SL(B≥A)≥0表示模糊数˜A的左边部分优于模糊数的左边部分，且

鬼医也不客套：“那在下就不客气了。”随手一指座下的小婢，说，“张兄，你这伤还得好生调养，这丫头跟了我几年，等闲御医也不及她，就暂留你府上，伤好之后，你再打发她走便是了。”

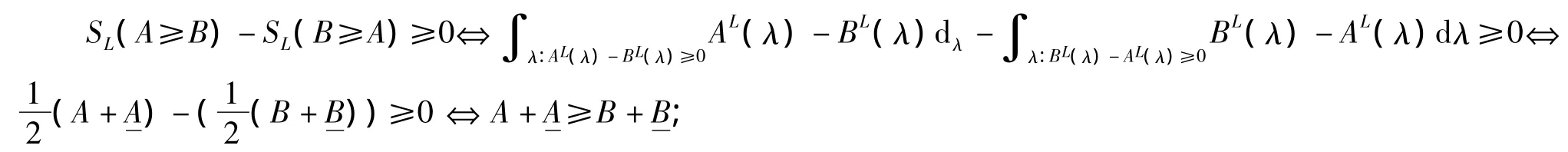
同理，SR(A≥B)-SR(B≥A)≥0表示模糊数的右边部分优于模糊数˜B的右边部分，且

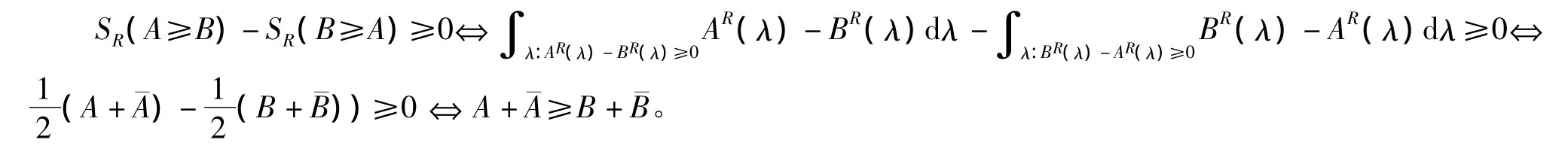
4 原问题的等价描述及求解过程

研究上述规划问题:模型(1)可等价于:

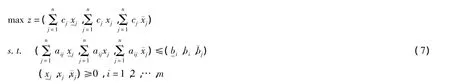
由三角模糊数的排序，模型(7)可转化为:

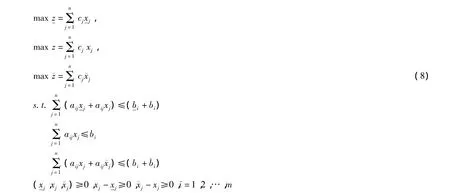
显然，模型(8)是一个具有3个目标的多目标线性规划问题，可用一般多目标线性规划的方法求解。要使三角模糊数)最大的关键在于应使尽可能大，前者目标具有更高的优先级。然后尽量大，后2个目标具有相同的优先级。从而问题(8)看成具有2个层次的多目标线性规划问题，且第1层线性规划问题为:

易求得(9)的最优解，设为(xj)*，j=1，2，…，n。

第2层次多目标线性规划问题为:

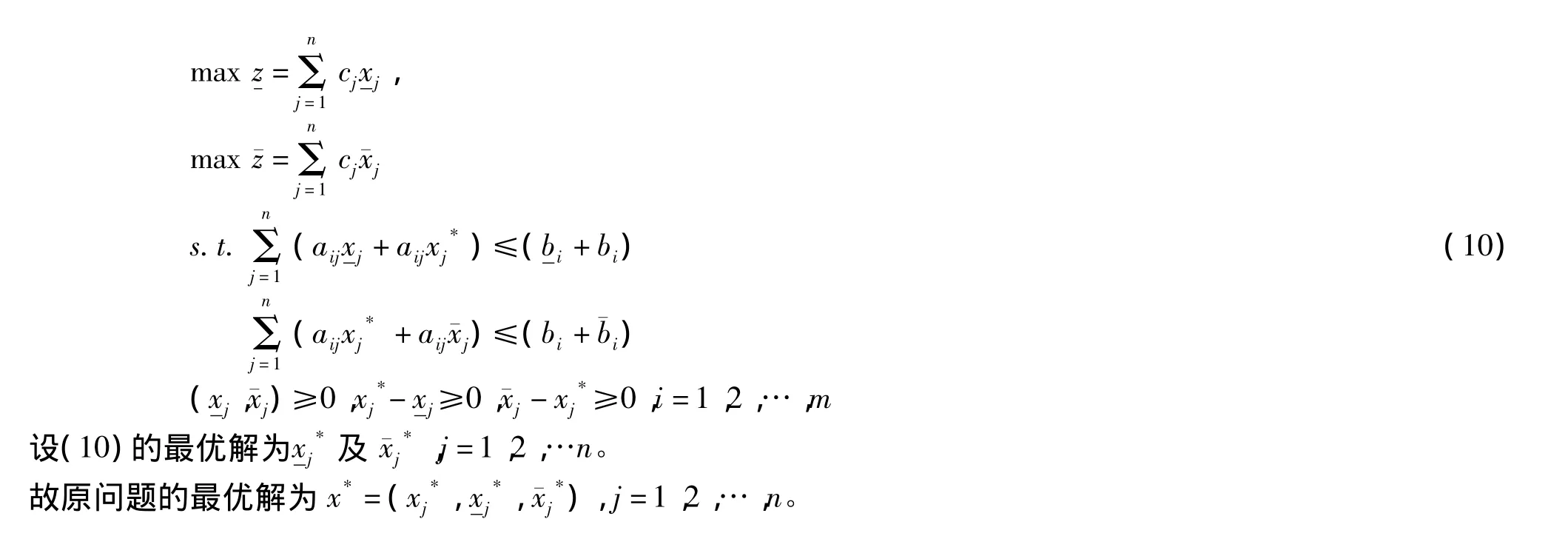
5 实例

考虑以下形式的模糊线性规划问题:

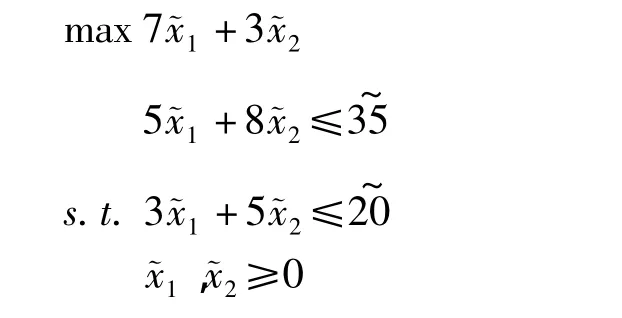
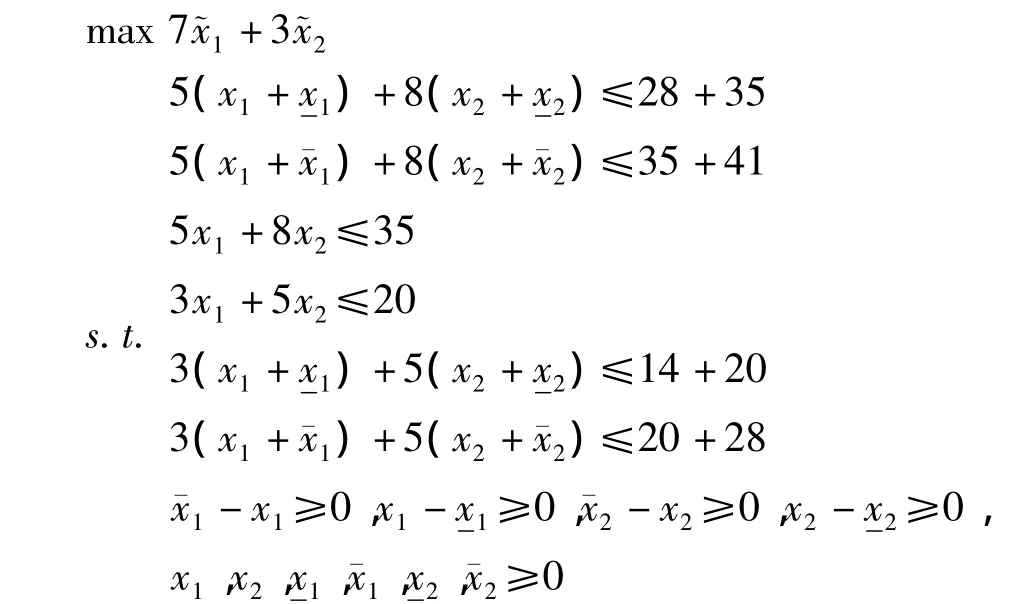
求得最优解为:

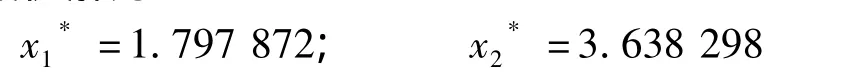
把以上的解代入得第2层多目标目标规划问题:

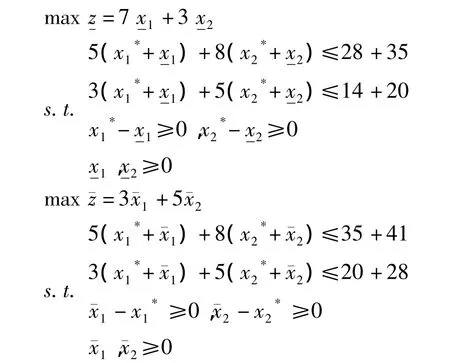
得到最优解为:

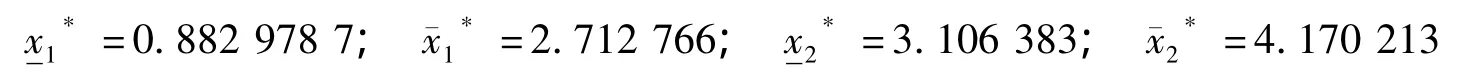
6 结语

本文讨论了变量为三角模糊数的模糊线性规划问题，利用比较优于面积的大小来确定三角模糊数的序关系，将一类变量为模糊数的线性规划问题转换成一个多目标线性规划问题，然后进一步转换成2层多目标线性规划问题，从而求出原问题的解答。目前对向量为模糊数的线性规划问题的研究还不是很完善，还需进一步研究。

［1］ZADETH L A.Fuzzy sets［J］.Information and Control，1965(8):338-353.

［2］TANAKA H，PRADE H.Banking fuzzy numbers in the setting of possibility theory［J］.Inform.Sci，1983(30):183-224.

［3］方述城，汪定伟.模糊数学与模糊优化［M］.北京:科学出版社，1997.

［4］朱章遐，曹炳元.具有模糊变量的线性规划问题［J］.模糊系统与数学，2008(2):115-119.

［5］胡宝清.模糊理论基础［M］.武汉:武汉大学出版社，2006.

［6］鲁成国.模糊数的比较与排序及其在多属性决策中的应用［D］.南宁:广西大学，2006.

［7］曾文艺，李洪兴，谷云东.模糊数的排序方法［J］.北京师范大学学报，2001，37(6):711-714.

［8］曾庆宁.模糊系数规划［J］.模糊系统与数学，2000，14(3):99-105.

［9］刘海涛，郭嗣琮.基于结构元方法的变量模糊的线性规划［J］.系统工程理论与实践，2008(6):94-99，128.

［10］王绪柱，单静.模糊量排序综述［J］.模糊系统与数学，2002，16(4):28-34.

A Study of Fuzzy Linear Programming Problems with Triangular Fuzzy Variables

CHENG Yali
(Information and Computing Science Department，Chengdu Electromechanical College，Chengdu 610071，China)

This paper discusses the fuzzy linear programming problem with triangular fuzzy variables.The order of triangle fuzzy number is decided by comparing the dominance area and then the solution to programming is simplified.Finally，the paper provides examples to testify the effectiveness of the solution.

Triangular fuzzy number;Fuzzy variable;Fuzzy linear Programming;Ranking;Dominance

O211

A

1008-5440(2011)03-0036-05

2011-03-24

成亚丽(1983-)，女(汉族)，山西高平人，助教，硕士，研究方向:优化与决策。