井喷失控条件下盐岩储库稳定性分析

马林建，刘新宇，许宏发，杨石刚，王子甲

（解放军理工大学 工程兵工程学院，南京 210007）

1 前 言

盐岩体是国际公认的能源（石油、天然气）存储的最理想介质。自全世界第一座盐岩地下储库在加拿大建成以来，国外共有盐岩溶腔储库已逾 44座，并平稳运行40年之久。国外盐岩介质中能源存储相关力学问题的研究经历了4个发展阶段[1]：（1）简单应用阶段（20世纪60年代初）；（2）模型研究与应用阶段（20世纪60年代中期至70年代初）；（3）数值模拟计算阶段（20世纪70年代末至90年代中期）；（4）损伤模型设计阶段（20世纪90年代中期至今）。随着我国“西气东输”配套工程江苏金坛储库建设工程起步及能源地下战略储备项目的兴起，国内学者掀起了对盐岩地下溶腔能源储库的稳定性分析和评价方面研究的热潮[2－5]。

现有的研究工作大多是基于储库平稳建设运营状态下盐岩溶腔稳定性分析，而极端灾害模式下的相关稳定性研究则鲜有涉及。尽管盐穴作为地下储库安全性比地面结构优良得多，但近30年来，国外灾储库泄漏、爆炸乃至盐穴失稳等灾难性事故时有发生。如2004年8月18日，美国德克萨斯州Moss Bluff储气库因密封系统失效造成天然气喷出，从而酿成持续4天的大火，烧烤半径达400英尺，事故致使价值至少3600万美元的天然气损失。由此开展极端条件下（战争、地震、恐怖袭击、压力失控）储库安全稳定性及灾害防护控制措施的研究成为国家能源战略储备安全的重大需求。本文通过数值模拟的手段，分析了建腔初期不同初始运营压力失控井喷条件下，储库溶腔腔周应力状态、损伤开展演化规律及变形收敛特征。

2 井喷失控工况解析

压力失控的极端情形是由于储气库密闭性失效、天然气泄漏起火爆炸导致的井喷灾难。井喷状态下井管中气体为瞬态流动，通过一维稳态流动假设可将问题简化为有摩阻作用的绝热管流问题。对于理想气体绝热管流运动适用摩阻作用欧拉方程为

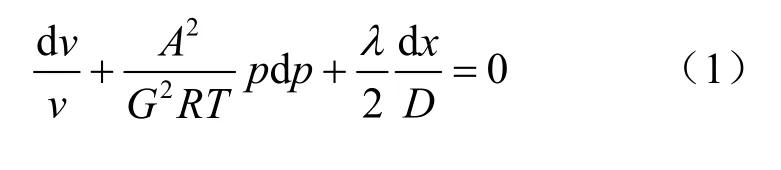
式中：p为气体绝对压力；v为气体截面流速；R为气体常数；T为气体热力学温度；λ为沿程阻力系数；A和D分别为井管截面面积和井管直径。

将上式沿管底截面积分到管顶截面可解得绝热管流质量流量公式为

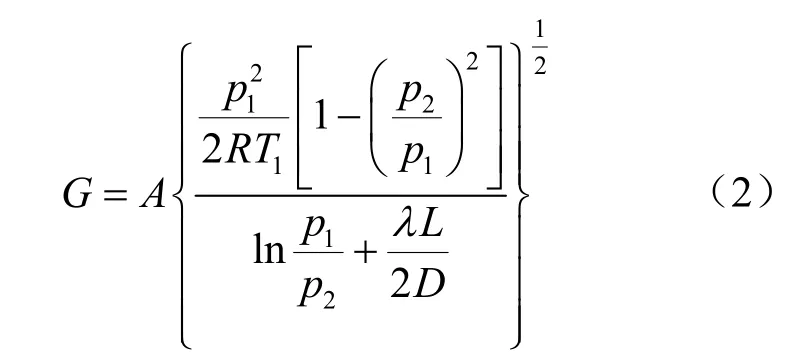
式中：L为井管管长；p1和p2分别对应于井管底部和井管口部的气体压强。

根据范诺线理论可知，在等截面管道中，摩阻作用总是使气流的速度趋于临界音速。 因此，无论进口截面（管底）气流是亚音速还是超音速，它们的极限速度都是临界速度，且临界状态只能出现在出口截面（管口）。将底部井口截面处气体压力取储气库内压（p =p1），截面流速为

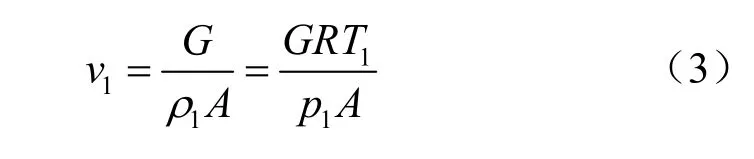
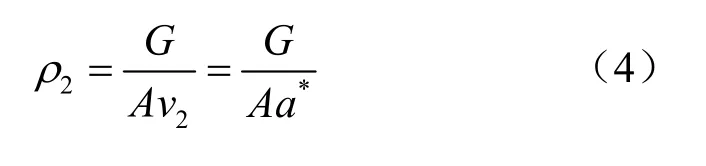
式中：a*为临界音速。

将式（2）～（4）代入绝热流动能量方程，有

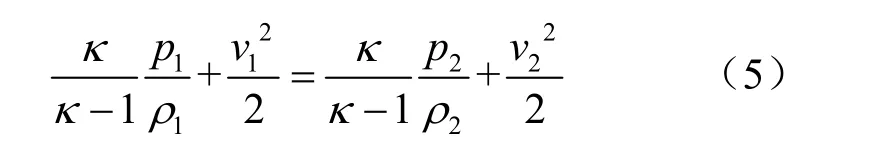
解得

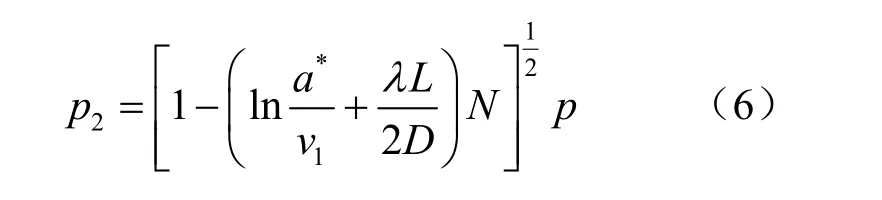
式中：κ为气体绝热指数；N为κ的函数。

联合式（6）与理想气体状态微分方程，对于特定的初始条件p(0)= p0，解得

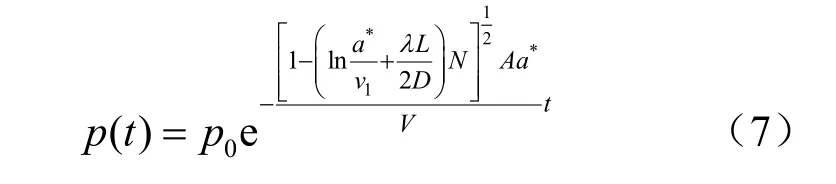
式中：p0为腔内气体初始压强，解析得到盐岩溶腔内压力下降随时间呈指数型降低。

结合我国金坛盐岩储库建设运营的实际工况，数值分析综合考虑水溶建腔(Ⅰ)、注气排卤(Ⅱ)和压力失控(Ⅲ)3个阶段。其中，建腔阶段的分析假定溶腔内压从初始地应力值线性减小至相应深度的饱和卤水压力，建腔周期为2年。建腔后的注气准备期为9个月，注气排卤阶段溶腔从饱和卤水压力线性上升至最大运营内压，周期为3个月。压力失控阶段根据式（7）分别考虑从17、12、7 MPa卸载至标准大气压的情况，具体工况如图1所示。

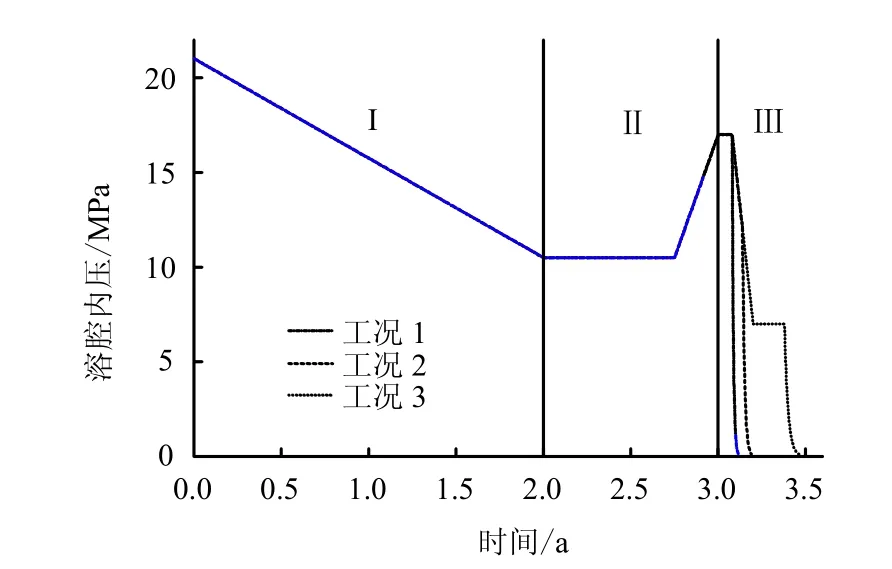
图1 计算工况Fig.1 Operating mode for simulation

3 模型建立

3.1 地质模型的建立

依据江苏金坛盐矿典型地层盐岩及夹层分布的钻井资料[6]，计算选取竖直方向高程1 333.2 m，从上至下依次为地表沉积层（433.2 m）、上覆泥岩层（400 m）、层状盐岩地层（158.4 m）和下卧泥岩层（341.6 m），盐岩层中泥岩夹层厚度分别为1.5、1.3、2.0、2.1 m。水平方向取约6倍溶腔直径范围（-300～300 m）。储库溶腔采用上下两个半椭球，中间接一理想圆柱体，高为98 m，半径为26 m，容积约为17×104m3。鉴于结构形式、荷载分布及边界条件的对称性，取1/4对称模型，采用六面体单元，网格在盐岩溶腔和夹层地段密集布置，精细到1 m 1个，共划分为317 920个计算单元。建模过程中，通过FLAC3D内置Fish语言调整软件内置基本形状网格节点坐标，实现模型网格的精确匹配。模型尺寸及网格划分见图2。

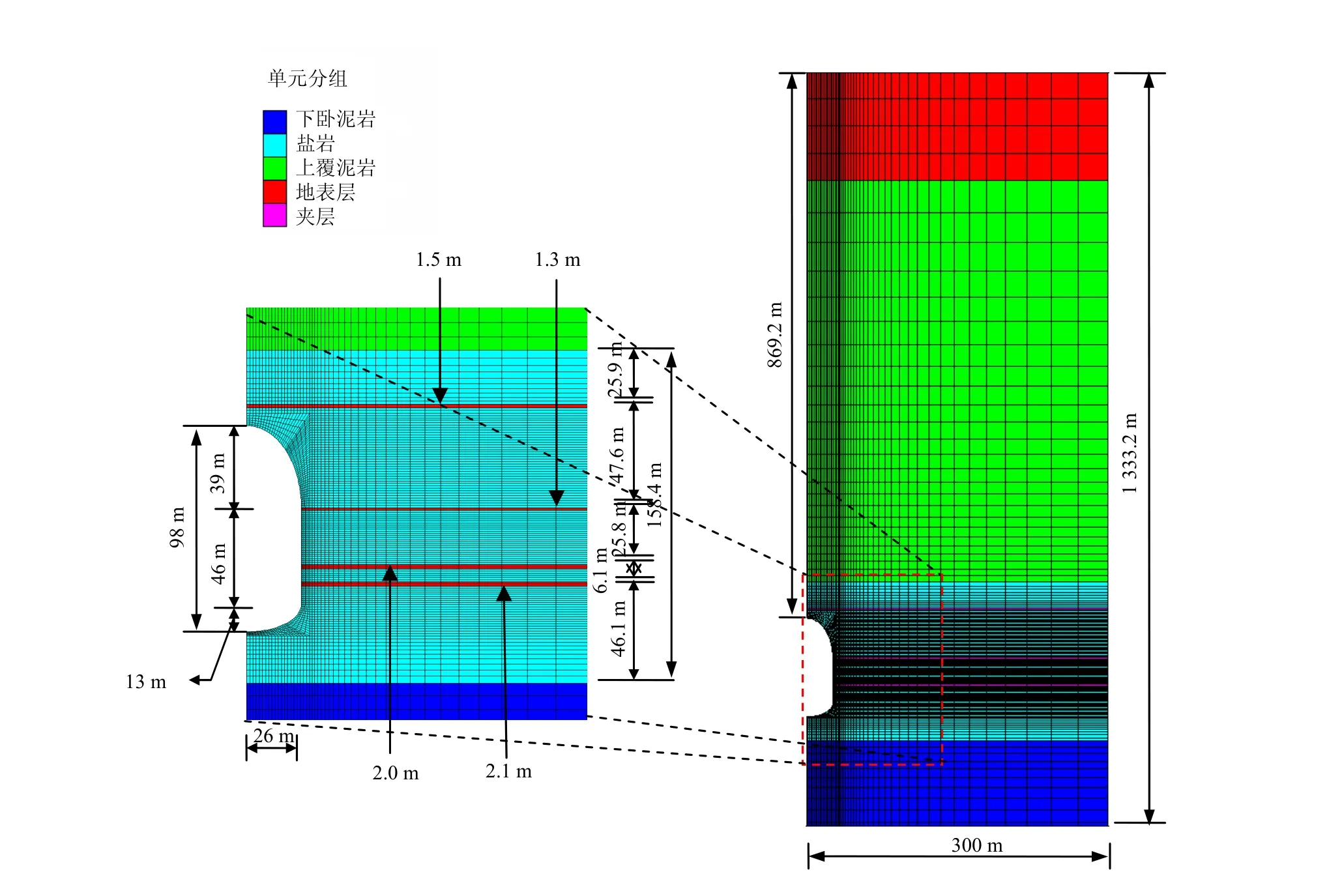
图2 计算模型尺寸及网格划分Fig.2 Model size and mesh division

3.2 蠕变模型及参数

DURUP[7]等通过对 Lemaitre、Norton-Hoff Power、Power、Transient Power、Munson-Dawson等经典盐岩本构模型对同一盐岩试验数据拟合对比，认为在不考虑温度的影响下，所有模型均能较好地匹配试验数据，相比较Munson-Dawson模型具有17个材料参数，Norton Power仅有2个材料参数，易从试验数据求得。因此，本文针对实际工程，选用简单实用的 Norton Power 模型描述盐岩的蠕变行为。

Norton材料模型(Norton)一般用于模拟盐的蠕变特性，标准形式为[8]

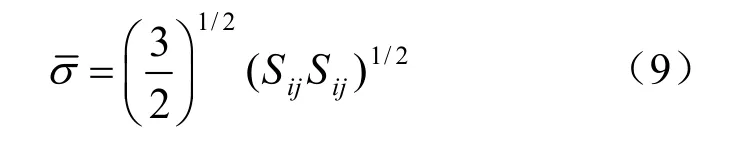
根据Mises应力定义及蠕变流动法则，盐岩稳态蠕变率的张量形式为

岩层的塑性行为可用Mohr-Coulomb屈服准则来判断（见图3）。以压应力为负，则剪切屈服破坏函数为

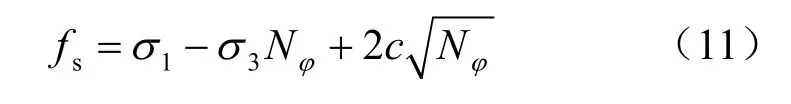
式中：Nϕ=(1+sinϕ)/(1-sinϕ)；σ1、σ3分别为最大和最小主应力；c、ϕ分别为岩石的黏聚力和内摩擦角。

考虑到层状盐岩张拉破坏特征，拉伸破坏屈服函数为

式中：σt为盐岩的抗拉强度。

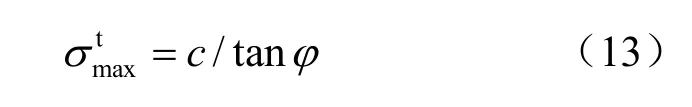
剪切破坏势函数采用不相关联流动法则，其表达式为

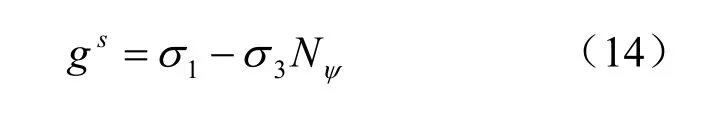
式中：Nψ=(1+sinψ)/(1-sinψ)，ψ为膨胀角。

拉伸破坏势函数采用相关联流动法则，其表达式为

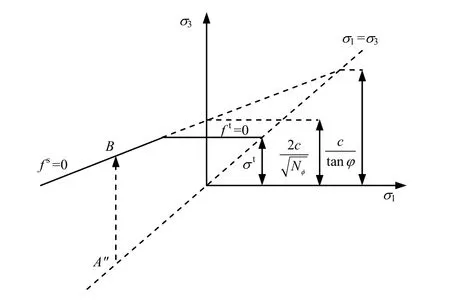
图3 Mohr-Coulomb屈服准则示意图Fig.3 Sketch of Mohr-Coulomb failure criterion

根据金坛盐岩试样（纯盐岩、含夹层盐岩和纯夹层）巴西劈裂、单轴三轴压缩和单轴三轴蠕变试验结果，参考国外盐岩储库计算所用参数，并考虑盐岩层、含盐夹层与泥岩层蠕变特性的差异，确定本文稳定性分析的参数如表1所示。

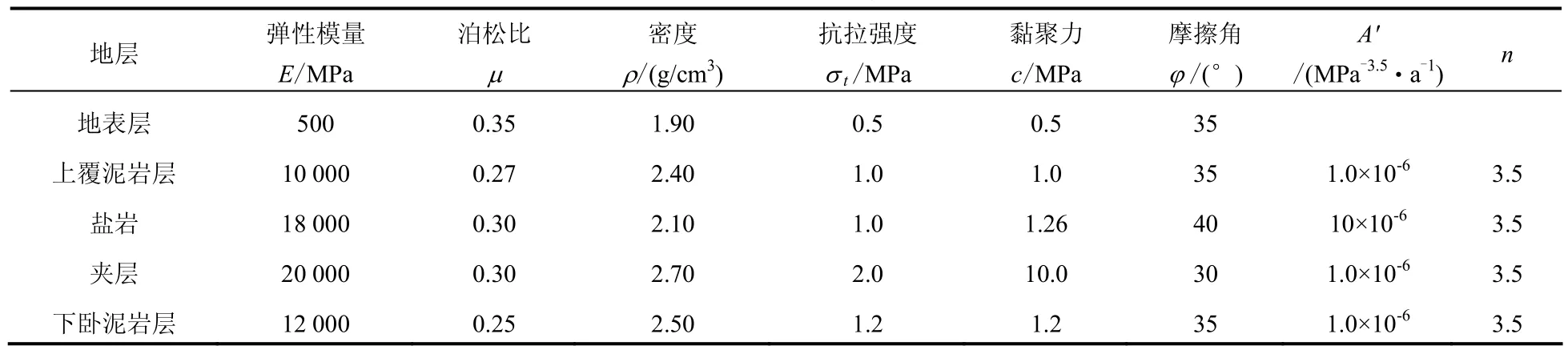
表1 储库稳定性计算参数Table 1 Parameters for storage cavern stability

4 计算结果及分析

4.1 应力场分析

图4给出了不同阶段（工况3）最大、最小主应力变化图。溶腔过程考虑腔体的流变，腔周未发现明显应力集中。同一区域最大、最小主应力差值不大，2倍洞径之外与初始地应力场趋于一致。但夹层位置产生一定集中度较高的拉应力区（以拉为正），腔周主应力等值线图被夹层隔断，这在最小主应力云图上更为显著。相同竖直位置夹层中最小主应力绝对值要低于盐岩层中的，而夹层中最大主应力绝对值则要高于盐岩层，即夹层位置最大剪应力要普遍高于盐岩层。注气排卤后应力场分布较建腔后变化不大。卸压阶段，腔周出现明显的应力集中，且随时间的发展不断加强；夹层位置拉应力区逐渐扩展，且应力集中程度加大。对比3种卸压工况，这种腔体较大范围的应力不均衡分布在低压卸荷时更为突出，因而对储库稳定性较为不利。

4.2 塑性区分布扩展

图5～7为3工况（17、12、7 MPa）卸压初始时刻(图 5(a)～图 7(a))、卸压中间时刻（图 5(b)～图7(b)）和卸压后（图5(c)～图7(c)）塑性区分布开展三维视图（视角与图8一致）。从图5(a)～图7(a)可清楚看到塑性区最先出现在夹层位置，屈服形式以拉伸屈服为主，并逐渐扩展成3条明显的屈服带。失控卸压阶段储库内腔塑性区向上下延伸直至连成一片，随后出现在腔顶和腔底部位，此时屈服以剪切屈服为主。卸压后塑性区布满全腔并向径向扩展一定厚度。腔的稳定性是不利的。

4.3 腔体蠕变变形

为分析失控卸压状态下储库变形特性及破坏规律，沿溶腔内表面腔顶、腔身和腔底部位布置了 7个监测点，如图8。

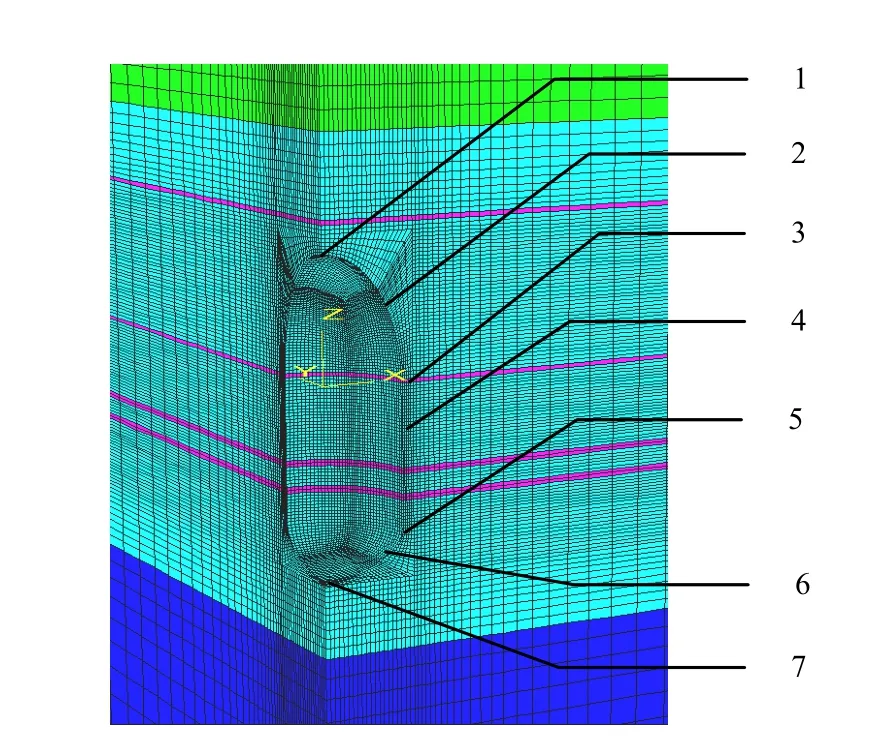
图8 盐岩溶腔监测点布置示意图Fig.8 Locations of measuring points of rock salt cavern

从关键部位位移监测时程曲线(图 9)及溶腔体积损失曲线(图10)可判定，储库处于整体流变收敛状态。建腔和排卤阶段溶腔收缩比较平缓，腔顶、腔腰和腔底最大位移为-0.497、-0.653、0.904 m，平均位移速率分别为-0.45、-0.6、0.82 mm/d；体积缩小6.06%，收敛速率V˙/V约为-0.005 %/d。卸压阶段溶腔监测点位移不断扩大，腔体加速收缩。据图10可知，最高运营压力下（17 MPa）失控卸压阶段储库体积减小量为 0.21%，平均体积减小速率为0.015 %/d；12 MPa下自由卸压使得储库体积缩小0.71%，平均速率为0.0358 %/d；7 MPa下卸压造成储库体积损失5.02%，则每天达0.142%是12 MPa下自由卸压的近4倍。

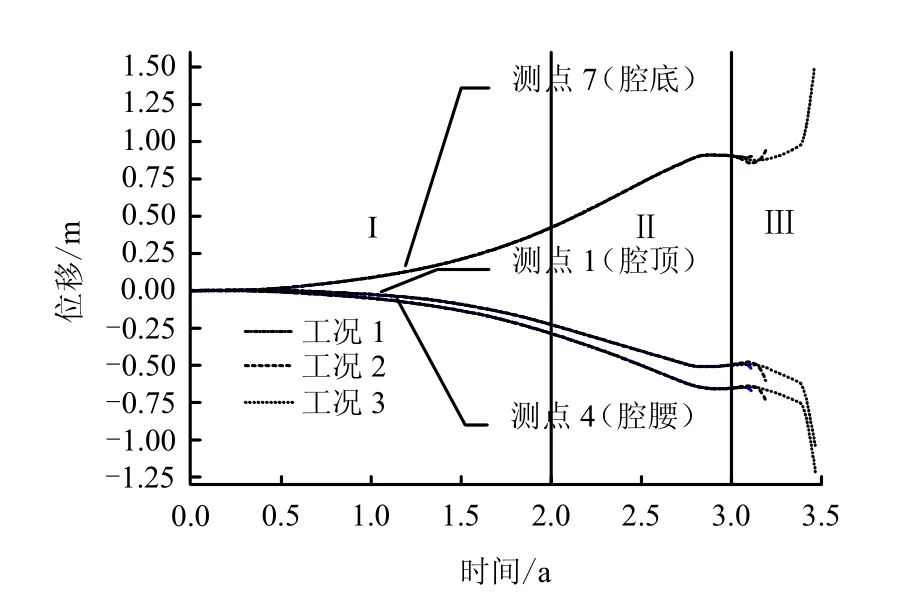
图9 腔周关键测点位移-时程曲线Fig.9 Curves of key measuring points displacements vs. time

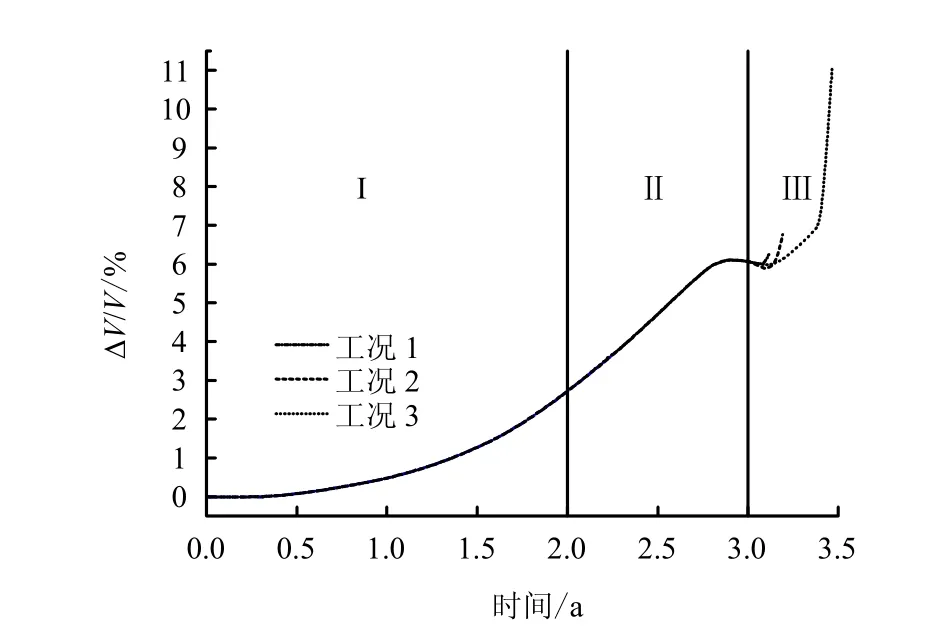
图10 腔体体积损失率曲线Fig.10 Cavern volume convergence curves

德国克劳斯塔大学研究建议[9]，一年循环周期下平均每天的体积减少应小于0.008 2%来保证正常运营阶段储气库的长期使用寿命。陈锋[10]通过数值计算得到恒定最低内压6.5 MPa时的体积减小速率约为0.004 5%/d，并假定降压时间占一个运行周期的1/3时间算得的降压阶段体积变化速率上限值为0.015 %/d。据此，只有最高运营压力下的自由降压才能保能储库的稳定。需要指出的是文献[10]认为体积收敛速率与降压速率呈线性关系，即体积损失速率随压降速率增加而线性增加，而本文得到的结论与此相反。分析原因，区别在于文献[10]所模拟的工况为正常运营压力范围（6.5～14.5 MPa）内，人为可控的不同降压速率对储库稳定性影响，相比本文研究的则是井喷自由卸压至标准大气压条件下储库的稳定性。因而，虽然高压井喷卸荷速率要高于低压卸荷情形，但溶腔内压按指数规律递减，卸压初始压力越低储库在低压维持的时间就越长（见图1），从而加速了储库的收敛变形。基于以上分析，失控自由卸压阶段储库稳定的关键因素为失控初始内压。

4.4 围岩应变速率分析

图11～13揭示了不同工况下，腔周单元应变速率的变化规律。水溶建腔阶段，腔顶、腔腰和腔底拉伸应变速率（以拉为正）分别在 4×10-3、1.0×10-3、3×10-3s-1以内；注气排卤后期，腔内岩体由拉伸转为压缩，最大应变速率各是-2×10-3、-1.48×10-3、-1.53×10-3s-1；失控卸压阶段，腔体内壁拉伸应变速率跃升至10-2s-1数量级。一般地，第Ⅲ阶段降压速率越快（高压卸荷）所获得的应变速率越高；同一降压速率之下腔顶和腔腰的应变速率要高于腔底，如12 MPa初始卸压下，腔顶、腔腰最大应变速率为 6.4×10-2、4.9×10-2s-1，腔底为 4.7×10-2s-1。通过最高与最低运营压力失控工况计算最终界定的腔周围岩应变速率的范围为：腔顶 1.0×10-2～7.2×10-2s-1，腔腰 1.0×10-2～7.5×10-2s-1，腔底1.0×10-2～5.3×10-2s-1。盐岩是具有较强流变特性的致密软岩。廖红建等[11]对硅藻质软岩进行了7.3×10-7～2.9×10-4s-1加载速率范围内的应变和应力控制式固结不排水三轴试验，结果表明，该软岩具有明显应变速率效应，其峰值强度和残留强度皆随着应变速率的增大而提高，轴向应变随时间的对数坐标近视呈线性增长趋势。此外，梁卫国等[12]针对层状盐岩矿床中 NaCl岩盐与无水芒硝盐岩，进行了10-5～10-3s-1范围内单轴压缩强度与变形特性的应变速率效应研究，研究表明，盐岩泊松比、峰值应变随加载应变速率增加而减小，其变形模量与应变速率呈对数关系，但强度和弹性模量基本不变。根据这一结论结合正常运营条件下盐岩储库应变率范围（10-5～10-3s-1），储库腔体稳定性是有所保证的。但失控阶段的腔体应变率相比稳定注采运行应变率增大了几十倍，10-3～10-1s-1应变率范围内盐岩的强度及变形特性对于失控井喷状态下储库的安全稳定至关重要，亟待开展进一步试验研究。

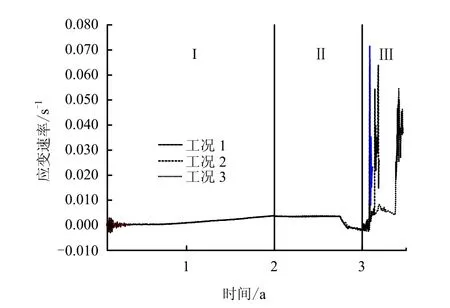
图11 腔顶单元应变速率时程曲线Fig.11 Top zone strain rate curves of storage cavern

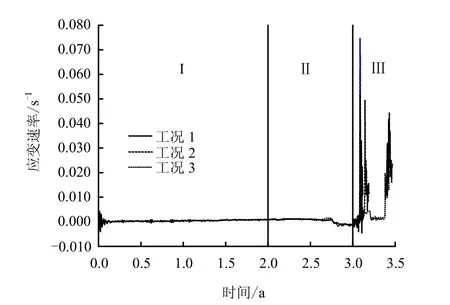
图12 腔腰单元应变速率时程曲线Fig.12 Middle zone strain rate curves of storage cavern

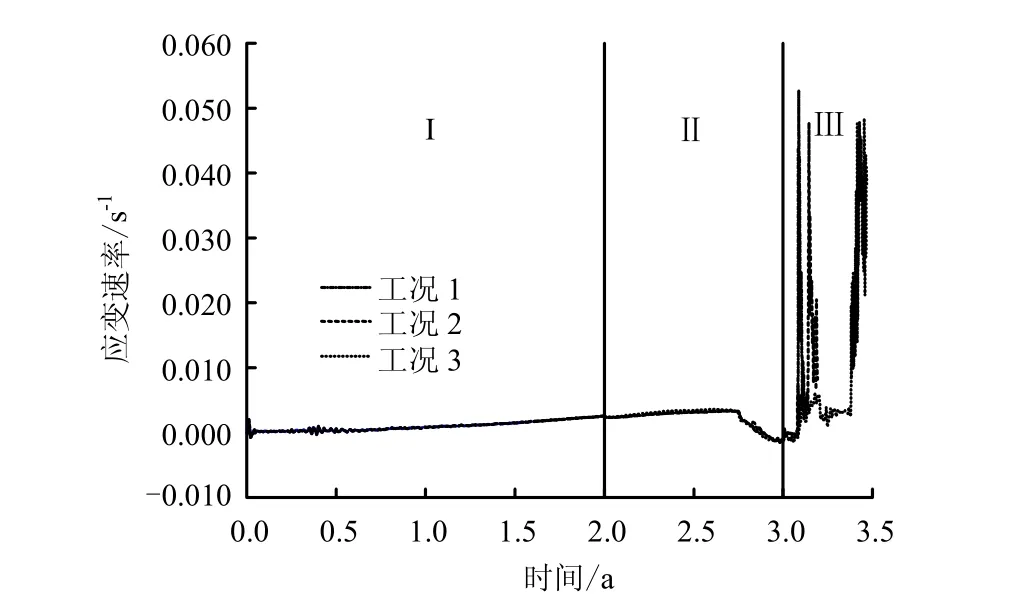
图13 腔底单元应变速率时程曲线Fig.13 Bottom zone strain rate curves of storage cavern

5 结 论

（1）建腔和排卤阶段，由于应变不协调硬夹层先行破损；失控卸压阶段，屈服区由夹层屈服带扩展直至布满整个腔体，卸压初始内压越小塑性区体积越大。对应的应力场变化表现为夹层位置出现拉应力区，卸压阶段腔周出现明显的应力集中，且随时间的发展不断加强；对比3种卸压工况，腔体较大范围的应力集中在低压卸荷时更为突出。

（2）硬夹层的存在一方面对储库的收敛变形起到了限制和加筋作用，有利于储库单腔的稳定；另一方面夹层部位的狭长破损区易于形成储库间的贯通造成储库密闭性实效，则对于储库腔群稳定性不利。

（3）17 MPa初始内压下失控卸压，储库平均体积损失率为0.015 %/d，12 MPa自由卸压储库体积损失率为0.035 8 %/d，7 MPa自由卸压储库体积损失率则高达0.142 %/d；根据克劳斯塔大学的研究建议，失控卸压仅发生在最高运营压力下才能保证储库的稳定性。

（4）相比建腔和排卤阶段，失控阶段腔体内壁围岩应变速率从10-3s-1级以内增大至10-2s-1级，属准静态范畴。10-3～10-1s-1应变率范围内盐岩的力学特性对于研究井喷失控状态下储库的稳定性尤为重要。

[1]吴文, 杨春和, 侯正猛. 盐岩中能源（石油和天然气）地下存储力学问题研究现状及其发展[J]. 岩石力学与工程学报, 2005, 29(增刊2): 5561－5568.WU Wen, YANG Chun-he, HOU Zheng-meng.Investigations on studied situations associated with mechanical aspects and development for underground storage of petroleum and natural gas in rock salt[J].Chinese Journal of Rock Mechanics and Engineering,2005, 29(Supp. 2): 5561－5568.

[2]陈卫忠, 伍国军, 戴永浩, 等. 废弃盐穴地下储气库稳定性研究[J]. 岩石力学与工程学报, 2006, 25(4): 848－854.CHEN Wei-zhong, WU Guo-jun, DAI Yong-hao, et al.Stability analysis of abandoned salt caverns used for underground gas storage[J]. Chinese Journal of Rock Mechanics and Engineering, 2006, 25(4): 848－854.

[3]陈锋, 杨春和, 白世伟. 盐岩储气库蠕变损伤分析[J].岩土力学, 2006, 27(6): 945－949.CHEN Feng, YANG Chun-he, BAI Shi-wei. Investigation on creep damage of natural gas storage in salt rock layer[J]. Rock and Soil Mechanics, 2006, 27(6): 945－949.

[4]尹雪英, 杨春和, 李银平. 泥岩夹层对层状盐岩体中储库稳定性影响[J]. 岩土力学, 2006, 27(增刊): 344－348.YIN Xue-ying, YANG Chun-he, LI Ying-ping. Influence of Mudstone Interlayers on stability of oil storage in laminates salt rock[J]. Rock and Soil Mechanics, 2006,27 (Supp.): 344－348.

[5]戴永浩, 陈卫忠, 杨春和, 等. 金坛盐岩储气库运营模型试验研究[J]. 岩土力学, 2009, 30(12): 3574－3580.DAI Yong-hao, CHEN Wei-guo, YANG Chun-he, et al. A study of model test of Jintan rock salt gas storage’s operation[J]. Rock and Soil Mechanics, 2009, 30(12):3574－3580.

[6]李银平, 尹雪英, 高敬. 中盐金坛压气蓄能电站工程初步可行性研究项目（地质）报告[R]. 武汉: 中国科学院武汉岩土力学研究所, 2007: 3－30.

[7]DURUP G G, XU J. Comparative study of certain constitutive laws used to describe the rheological deformation of salts[C]//The Mechanical Behavior of Salt Proceedings of the Third Conference. France: Trans Tech Publications, 1993: 75－83.

[8]Itasca Consulting Group Inc. FLAC3D(Version 2.1)users manual[M]. USA: Itasca Consulting Group Inc., 2002.

[9]侯正猛. 金坛地下储气库15口采卤溶腔稳定性评价技术服务报告[R]. 德国: 克劳斯塔大学, 2004: 18－25.

[10]陈锋, 杨春和, 白世伟. 盐岩储气库最佳采气速率数值模拟研究[J]. 岩土力学, 2007, 28(1): 57－62.CHEN Feng, YANG Chun-he, BAI Shi-wei. Investigation on optimized gas recovery velocity of natural gas storage in salt layer by numerical simulation[J]. Rock and Soil Mechanics, 2007, 28(1): 57－62.

[11]廖红建, 蒲武川, 殷建华. 软岩的应变速率效应研究[J].岩石力学与工程学报, 2005, 24(18): 3218－3223.LIAO Hong-jian, PU Wu-chuan, YIN Jian-hua. Study on strain rate effect of soft rock[J]. Chinese Journal of Rock Mechanics and Engineering, 2005, 24(18): 3218－3223.

[12]梁卫国, 徐素国, 莫江, 等. 盐岩力学特性应变率效应的试验研究[J]. 岩石力学与工程学报, 2010, 29(1): 43－50.LIANG Wei-guo, XU Su-guo, MO Jiang, et al. Test study of strain rate effects on mechanical performances of salt rock[J]. Chinese Journal of Rock Mechanics and Engineering, 2010, 29(1): 43－50.