并行CRC在FPGA上的实现

莫元劲，黄水永

（广州数控设备有限公司 广东 广州 510165）

循环冗余码校验CRC广泛用于通讯领域和数据存储的数据检错。很多时候，人们往往选择C语言来实现CRC对数据的校验检错，实现起来也比较简单，但是其流水线处理方法大大限制了对数据流处理的速度。随着FPGA的大量普及，并行处理数据有着传统流水线无可比拟的巨大优势。使用超前位并行计算方法计算CRC，对通讯领域和数据存储的快速数据处理有着重要的意义，笔者根据超前位计算方法得到在FPGA上面的并行CRC通用计算方法，并可以根据需要，实现数据级联计算，得到快速计算数据流的CRC方法。

1 CRC编码解码原理

1.1 CRC编码

设 M（x）为信息多项式，G（x）为生成多项式，得到的 CRC位数为 r，则 M（x）左移 r位，作模 2 除法，得到的商为 Q（x），余数多项式R（x）即是信息多项式的CRC校验码，数学表示为[1]：

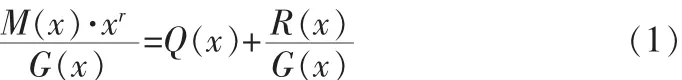
1.2 CRC解码

为确保数据信息的正确性，信息数据经过CRC编码得到CRC校验码，校验码和信息数据一起进行数据封装。如图1所示。

图1 CRC校验数据封装Fig.1 CRC data check frame

读取信息数据加CRC校验码的时候，再用相同的生成多项式进行校验，若校验结果不正确，那证明数据信息丢失或者已经被破坏。数学表示为：

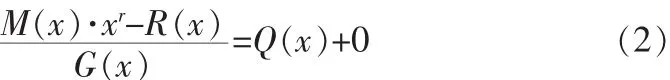
余数多项式结果为0为正确[2]，其余结果都说明数据不正确（有些像IEEE802.3中的CRC，因为特别的取反处理，余数多项式不是0，而是等于0xC704DD7B[3]）。典型CRC在FPGA上的应用如图2所示[4]。

2 串行CRC编码解码实现

CRC的编码解码可由一般的串行流水线算法来获得，但是很多时候硬件接口串行的，并行接口也进行串行流水线的CRC计算显然不合理。如：最常用的CRC32生成多项式为：G（x）=x32+x26+x23+x22+x16+x12+x11+x10+x8+x7+x5+x4+x2+x+1[5]，串行流水线的硬件实现如图3所示[4]：

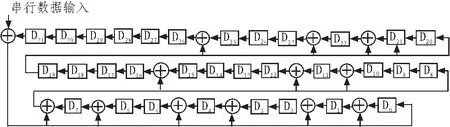
图3 串行CRC32硬件实现Fig.3 Serial CRC32 hard ware

（图3中的Dx为D寄存器，⊕为异或运算。）由图（3）可见，要处理n个数据输入就要延迟n个时钟周期才能得到CRC的校验码。而且很多时候往往硬件接口不是串行数据输入，而是并行数据输入，这就要求要把数据流进行并行串行转换，处理来很麻烦，不能满足数据流的快速处理。下面介绍一种可以在硬件上实现，基于FPGA并利用超前位计算方法得到任意长度数据的并行CRC计算方法。该算法使得数据量很大的数据流可以在数据接收或者发送的开始时候就可以计算其CRC的校验值，而不是把整个需要校验的数据放到缓存区再开始计算校验值，达到真正的并行数据处理目的。

3 并行CRC的实现

具体的算法描述如下：

假设数据输入的位宽为m，第n个周期输入数据为：

假设CRC生成多项式阶数为r：

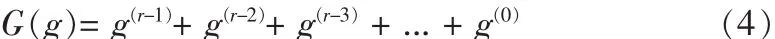
假设第n-1个周期计算得到的CRC校验码为

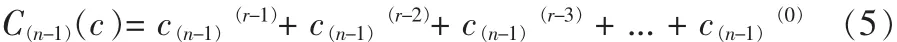
为了计算得到对应第n个周期的数据输入Dn（d）的CRC校验值 C（n）（c），首先把第 n 个周期输入数据 Dn（d）左移 r位，扩展为（m+r）位，其中低 r位补 0，即：

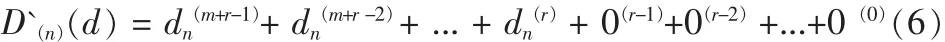
同时，实现级联运算，把第n-1个周期计算得到的CRC校验码 C（n-1）（c）合到第 n 个周期要计算的数据里面，进行模 2除法计算得到 CRC 校验值 C（n）（c）。根据公式（1），C（n）（c）作为第n个周期的余数，那么有第n个周期要进行模2除法计算的数据为：

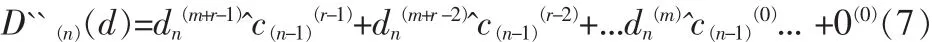
（注：^为异或运算符号。）

为了快速实现模2除法，算法应用了一种超前位计算方法。对于该超前位计算方法，利用模2除法运算方法，首先判断 D``（n）（d）的最高位 dn（m+r-1）^c（n-1）（r-1）是否为 1，若 dn（m+r-1）^c（n-1）（r-1）为 1 则进行除数为 CRC 生成多项式 G（g）的模 2 除法；若最高位 dn（m+r-1）^c（n-1）（r-1）为 0，那么把除数 G（g）当作 0，再作模 2除法，得到计算结果 D```（n）（d），即其运算如图 4所示：

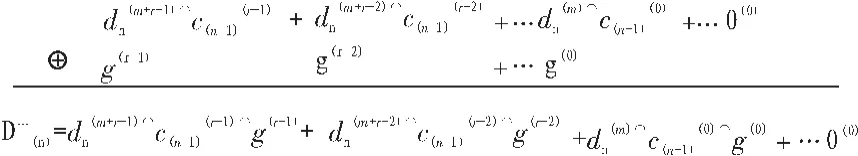
图4 模2除法运算结果Fig.4 Result of module-2 division

然后 ，判断 D```（n）（d）次高位 dn（m+r-2）^c（n-1）（r-2）^g（r-1）是否为1，再进行下一步的计算，其运算过程与 D``（n）（d）最高位的判断计算一样，直至到第r步，最后得到的余数则为该数据的CRC校验值。

对于最高位的判断运算，因为CRC生成多项式G（g）的最高位 g（r-1）为 1，所以不管 dn（m+r-1）^c（n-1）（r-1）是不是 1，作模 2除法的结果是 D```（n）（d）的最高位为 0。 也就是说，不管 D``（n）（d）的最高位 dn（m+r-1）^c（n-1）（r-1）是否为 0，经过第一步计算，其结果都是 D```（n）（d）的最高位为 0。

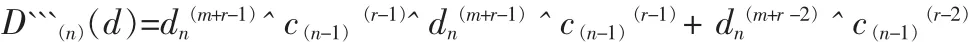
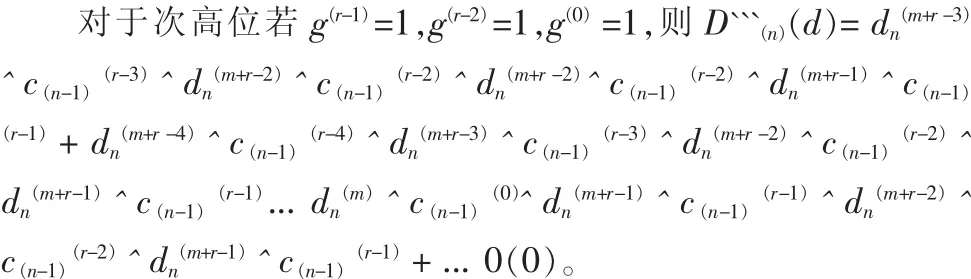
同理，对于余下的r-2次运算采用相同的计算方法进行递推。计算完r次之后，得到的数据就是第n个周期输入数据Dn（d），并且第n-1个周期计算得到的 CRC校验码为C（n-1）（c）时，对应 CRC 生成多项式 G（g）的 CRC 校验值C（n）（c）。

例如，假设输入数据宽度为8位，CRC生成多项式的为G（g）=g5+g4+g3+1，那么根据上述算法可以得到在FPGA上面的函数实现代码如下：

程序中，DATA_in为8位的数据输入，CRC_last为上次的CRC校验值，CRC5_D8为CRC计算结果输出。

如果要实现任意长度的数据CRC校验，则只需要把上次的数据输入得到的CRC校验码作为本次CRC校验码输入，那样就可以进行级联，计算得到任意长度的数据CRC校验码。

此算法充分利用FPGA的并行处理能力和数学算法上的超前位计算原理实现快速有效的CRC计算，与传统的流水线法、矩阵法[6]等相比有非常大的优势。该算法对于任意宽度的数据输入，和任意生成多项式也都通用，非常灵活，并且算法是基于递推方法，FPGA的程序也可以由软件语言VC++，VB等来生成得到，使用非常方便实用。

4 结果与仿真

使用的FPGA芯片为ALTERA公司的低端芯片EP1C6T144I7，其运算速度最快可达320 MHz，也就是说 3.2 ns的时间就可以把8位的数据的CRC校验码计算出来。实现级联的计算，如在图5中，连续输入数据流0x35、0x65、0x9A、0x3F、0x65、0x10、0xBB、0x8C、0x27、0XB9、0x97、0x8D、0x2C，在刚接完最后一个数据0x2C时候就可以得到这一串数据流的CRC校验值0x08。对比要接收完整个数据流再作相应的CRC计算有极大的优势。同时使用的FPGA资源非常少，只用了23个逻辑单元，很好地做到速度与资源的平衡。采用更高端的FPGA芯片，速度更高，此算法完全可以满足10 Gbit的以太网数据的CRC校验计算。

图5 实现级联的CRC仿真结果时序图Fig.5 simulated CRC timing of data sequence

5 结束语

以上算法对于任意位数据输入，任意生成多项式都可通用，任意长度的数据通过级联可以得到CRC校验码输出，并且采用并行处理和超前位计算，达到非常高的运算速度。其算法的FPGA实现应用也非常广泛，不论是一般的串行数据通讯，还是100 M，1 000 M甚至10 GM的以太网都可以用到。对此Xilinx，Altera等FPGA公司都开发了相关的IP（知识产权）。本算法已经成功用于FPGA上的串行数据发送及1 000 MHz/100 MHz以太网等通讯，达到快速处理数据流检错的效果。

[1]曹志刚，钱亚生.现代通讯原理[M].北京：清华大学出版社，1992.

[2]常天海，胡鉴.基于FPGA的CRC并行算法研究与实现[J].微处理机，2010，4（2）:45-48.

CHANG Tian Hai，HU Jian.Applicating research of CRC parallel algorithm base on FPGA[J].Microprocessors 2010，4（2）：45-48.

[3]Chris Borrelli.IEEE 802.3 Cyclic Redundancy Check[S]2001.

[4]Sunita Jain&Guru Prasanna.在Virtex-5 FPGA中使用CRC 硬模块[EB/OL]（2008-12）.http://www.doc88.com/P-38579361672.html.

[5]ISO/IEC.IEEE Std 802.3 2000 Edition.Part3.Carrier sense multiple access with collision detection （CSMA/CD）access method and physical layer specifications.[S].2000.

[6]刘昭，苏厉，金德鹏，等，10G以太网系统中的并行CRC编解码器设计[J].电子技术应用，2004，30（4）：47-50.

LIU Zhao，SU Li.，JIN De-peng，et al.Parallel CRC Coder and Decoder Designed in 10G Ethernet System.[J].Application of Electronic Technique，2004，30（4）：47-50.