不同裂隙相对张开度下类岩石材料断裂试验与破坏机理

(中南大学 资源与安全工程学院，湖南 长沙，410083)

裂隙岩体是水利、交通、采矿、石油开采等工程中边坡、地下洞室问题中广泛遇到的一类复杂工程介质[1]。考虑到大型现场试验的困难，现有的针对实际裂隙岩体破坏过程的研究主要借助于室内类岩石材料(如石膏、砂浆)模型试验进行[2]。于骁中等[3]对于理论分析含裂隙岩石和混凝土结构的断裂破坏机制进行了研究；20世纪末，国内外学者着手于预制裂隙岩石及类岩石材料的实验分析及理论研究工作[4−17]，如：关宝树等[6]采用预制小块体堆砌的方法在模型中制作贯通裂隙，对不同倾角裂隙试样的强度分布规律进行了试验；张平[7]采用预埋插片制作闭合裂隙试件，对动静载荷作用下裂隙两两间的扩展、贯通过程及影响因素进行了分析；Wong等[12−13]通过预制 2条裂隙石膏试件在单向及双向静力加载条件下的实验，研究裂隙岩体的断裂破坏机理。近年来，国内外许多学者在类岩石材料领域内所取得的研究结果[10−17]都表明：岩石和混凝土的断裂力学理论可以用于解决这类材料的断裂破坏问题。现阶段对于预制1条或2条倾斜裂隙的类岩石材料断裂破坏规律及裂隙尖端微裂纹起裂、扩展机理的研究[8−17]比较成熟，并且在实验过程中得到了验证，但是，对于预制1条水平裂隙材料的断裂破坏实验及机理的研究较少。本文作者根据相关试验，结合数值分析结果，探索预制1条水平裂隙的类岩石材料断裂破坏机制。

1 断裂破坏试验

1.1 材料制备

为了模拟裂隙岩体在单轴压缩下的破坏特征，本实验采用与岩石相似(脆性、剪胀)的模型材料(白水泥、细沙和水)制作类岩石模型试样。加入细沙一方面可作为模型试样的骨料，另一方面可增加模型材料的摩擦性能；模型试样所用各组分配比为：V(白水泥):V(细沙):V(水)=2:1:1(体积比)，细沙由孔径为1.05 mm的筛筛分后使用；试验模具各组件全部采用8 mm厚的有机玻璃制作，并用玻璃胶黏结、拼装成型，成型模具内部尺寸(长×宽×高)为150 mm×30 mm×200 mm。预制裂隙采用试件养护初期拔出铝合金薄钢片的方法制作，薄钢片尺寸(长×宽×高)为40 mm×20 mm×0.4 mm。裂隙位于材料体中部，如图1所示。

1.2 加载装置

试验加载装置采用高精度能控制加载速度的电液伺服控制试验机，利用DCS—200加载控制系统软件，在200 N/s的力控加载速度下，观察并记录试件加载过程中裂隙尖端变形特性及试件整体破坏模式。在实验过程中，在试件上、下受压端与机头钢块之间布置预先涂抹黄油的橡皮垫，以减弱端部效应的影响；在试件中部放置千分表，以表征试件受压过程中的横向变形特性。

图1 类岩石试件裂隙布置图Fig.1 Distribution pattern of crack in rock-like specimen

2 实验结果与分析

在试验过程中发现：预制贯通裂隙类岩石材料整体破坏主要有2种模式：裂隙尖端屈服破坏和裂隙中部受拉破坏。

裂隙尖端屈服破坏如图2所示。这类破坏模式是以裂隙尖端屈服破坏后引起试件斜对角线上的最大剪应力破坏为主，试件在破坏过程中表现出比较明显的塑性特征。裂隙尖端裂纹发育时间比较迟，尖端微裂纹出现后缓慢扩展，直至试件整体破坏前并无明显裂纹加速扩展迹象，整个破坏过程持续时间为3～5 s，在此破坏模式下能够观察到裂纹的起裂、扩展过程；在裂纹发育前，试件横向变形开始加速，但是，横向总变形量不大。

裂隙中部受拉破坏如图3所示。这类破坏模式以裂隙面中部材料受横向拉伸作用下的受拉破坏为主，在试件破坏过程中，材料塑性特征表现不明显。在加载初期，裂隙中部垂直裂隙面方向上出现长度较短、张开度较小的微裂纹；微裂纹出现后并没有继续扩展，而是处于停滞状态，持续时间为7～9 s，此阶段试件的横向变形增长缓慢；继续加载，微裂纹开始加速扩展，直至试件整体发生破坏，这一过程持续时间不足2 s，且横向变形加速比较明显，破坏前试件横向总变形量比较大，在此破坏模式下，裂隙尖端没有明显破坏迹象。

图2 裂隙尖端屈服破坏模式图Fig.2 Model graph of yield-failure in crack tip

图3 裂隙中部受拉破坏模式图Fig.3 Model graphs of tension-failure in the middle of crack

图4 混合破坏模式图Fig.4 Model graphs of mixed-failure

在实验过程中，存在介于2种破坏模式之间的实验现象(如图 4所示)。在加载初期，裂隙中部垂直裂隙面方向上出现长度较短、张开度较小的微裂纹，发育一定程度后扩展停滞；继续加载，位于裂隙面上部的竖向微裂纹逐渐消失，同时在裂隙左端点出现微裂纹，并沿加载方向向上扩展；加载继续进行，裂隙面下部的竖向微裂纹也开始消失，同时在裂隙右端点出现微裂纹，并沿加载方向向下扩展，在此之后继续加载，试件呈现出与第1种破坏模式相似的破坏过程。

3 数值计算与结果分析

通过对试件制作过程及试验结果分析，认为试件后期养护过程中，依靠水泥砂浆水化反应发热膨胀致使裂隙面闭合[1]的实验方法不可靠[17]，这种闭合裂隙生成方式不能保证裂隙面完全闭合，本文作者认为这是影响本次试验中裂隙体破坏模式不同的主要原因。

基于上述分析，假定裂隙体材料养护过程中裂隙面依然保持平面，但其闭合程度并不相同。为描述裂隙闭合形态，引入相对张开度β(即裂隙张开度/裂隙长度)，应用 FLAC3D数值分析软件，基于应变软化本构模型，对本次试验所用模型进行分析计算。模型参数见表 1。观察并记录裂隙尖端周边单元的应力分布状态以及相对张开度对裂隙尖端邻域内应力强度的影响规律，并结合裂隙尖端邻域内渐进应力解析解，探求裂隙尖端渐进应力场分布理论在含有1条预制水平裂隙的类岩石试件受单向均布压荷载作用下的适用范围。

表1 数值模型参数Table 1 Parameters for numerical models

3.1 裂隙相对张开度β对试件破坏模式的影响

裂隙尖端水平方向上0～1 mm邻域内8个单元的应力状态结果见图5。

从图5可知：当β小于0.002 5时，裂隙尖端微小邻域内有应力集中现象，且随着β的减小而增大；对该组数据拟合后发现：随着r的增加，其强度呈指数函数减小；当β大于0.010 0时，裂隙尖端邻域内没有出现渐进应力解析解中的应力集中现象，在加载初期，其应力比较低，甚至出现拉应力；而β取0.005 0时，裂隙尖端邻域内既没有应力集中现象，也没有出现拉应力单元，分析范围内应力强度变化并不明显。可见：β取值0.005 0可以看作2种破坏模式的分界值；当β＜0.005 0时，试件发生以裂隙尖端屈服引起的斜对角线上最大剪应力破坏模式为主；当β＞0.005 0时，试件发生以裂隙中部岩体材料受横向拉伸破坏模式为主；当β=0.005 0时，试件发生介于2种模式之间的破坏形式。

图5 β影响下裂隙尖端邻域内σxx的数值解Fig.5 Numerical solution σxx in neighborhood of crack tips affected by parameter β

3.2 裂隙相对张开度β对裂隙尖端渐进应力分布理论适用范围的影响

根据裂隙尖端邻域内渐进应力分布理论，含有张开裂纹的裂隙体在单向均布荷载p作用下(如图 6所示)，当a=0°时，裂纹尖端邻域内渐进应力表达式为：

图6 单向均布荷载p作用下裂隙面应力分布状态Fig.6 Stress state in face of crack under uniaxial compression

式中：p为竖向均布荷载；a为裂隙长度的一半；θ和r为以裂隙尖端为原点，裂隙延伸方向为正方向建立的极坐标系。

以σxx为算例，对式(1)关于θ求导，得θ=0°时σxx取得最大值，即：

据式(2)可以判断裂隙尖端 0°方向上会出现σxx的应力集中现象，而当β≥0.005时，数值模拟结果显示并没有出现裂隙尖端邻域内的应力集中现象，因此，此情况下式(2)不再适用。根据式(2)计算裂隙尖端应力强度，并从数值计算结果中提取β=0.001 0与β=0.002 5时裂隙尖端相应应力强度，并将其分列于表2与表3中。

表2 β=0.001 0时裂隙尖端邻域内σxx的解析解与数值解Table 2 Numerical and theoretical solution of σxx in neighborhood of crack tips (β=0.001 0)

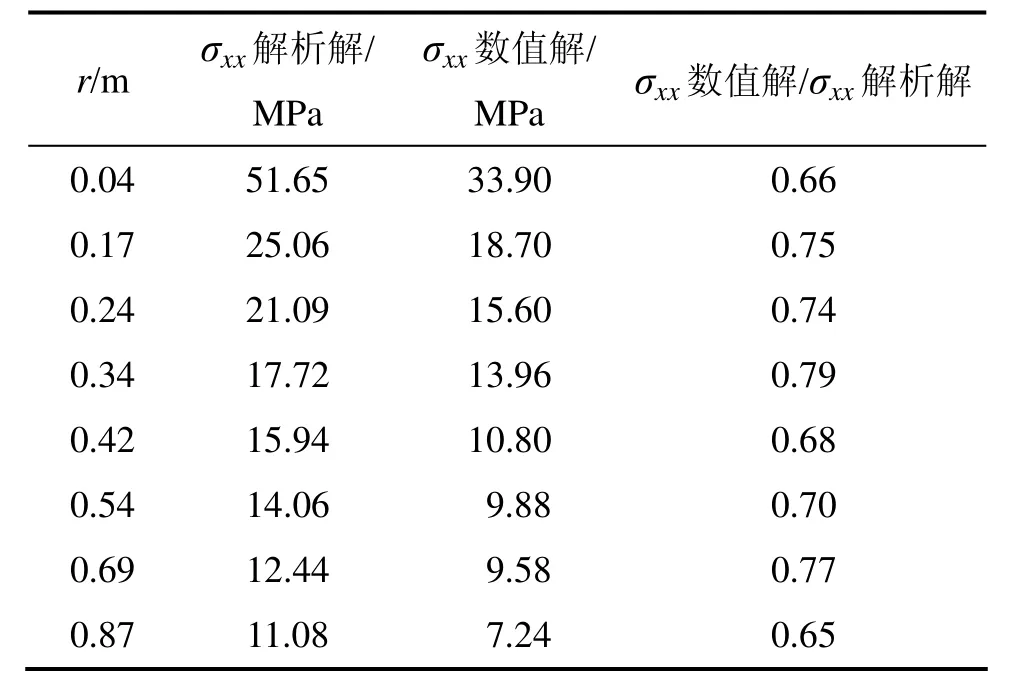
表3 β=0.002 5时裂隙尖端邻域内σxx的解析解与数值解Table 3 Numerical and theoretical solution of σxx in neighborhood of crack tips (β=0.0025)

对比表2与表3可知：裂隙尖端极限应力强度与β有关，β较小时，裂隙尖端的应力集中现象较明显，应力更接近于渐进应力解析解。除裂隙尖端外，在对尖端附近邻域内的极限应力强度求解时，需要对裂隙尖端邻域内渐进应力解析解进行折减计算，本次试验中，试件的折减系数为0.73。

4 结论

(1) 单向均布压应力作用下含有 1条预制水平裂隙的类岩石材料，根据其预制裂隙闭合情况的不同而呈现不同的破坏模式：裂隙尖端屈服引起的斜对角线上最大剪应力破坏和裂隙上部材料受横向拉应力作用引起的拉伸破坏，2种破坏模式的β临界值在0.005 0附近。

(2) 当β≤0.002 5时，应用渐进应力分布公式计算含有1条水平裂隙的类岩石材料裂隙尖端邻域内的极限应力强度时，需要对应力强度解析解进行折减，据此计算得到本次试验条件下的折减系数为0.73；当β≥0.005 0时，裂隙尖端邻域内渐进应力分布理论预言的裂隙尖端应力集中现象没有出现，此时，该理论公式不再适用。

[1] 李宁, 张平, 陈蕴生. 裂隙岩体试验研究进展与思考[C]//中国岩石力学与工程学会第七次学术大会论文集. 西安: 中国科学技术出版社, 2002: 63−69.LI Ning, ZHANG Ping, CHEN Yun-sheng. The progress and thought of the experimental study for the cracked rock mass[C]//Proceedings of the 7th Rock Mechanics and Engineering Conference. Xi’an: China Science and Technology Press, 2002,63−69.

[2] 张平, 李宁, 贺若兰. 含裂隙类岩石材料的局部化渐进破损模型研究[J]. 岩石力学与工程学报, 2006, 25(10): 2043−2050.ZHANG Ping, LI Ning, HE Ruo-lan. Research on localized progressive damage model for fractured rocklike materials[J].Chinese Journal of Rock Mechanics and Engineering, 2006,25(10): 2043−2050.

[3] 于骁中, 谯常析, 周群力. 岩石和混凝土断裂力学[M]. 长沙:中南工业大学出版社, 1991: 10−35.YU Xiao-zhong, QIAO Chang-xi, ZHOU Qun-li. Rock and concrete fracture mechanics[M]. Changsha: Central South University of Technology Press, 1991: 10−35.

[4] 黄明利. 非均匀岩石裂纹扩展机制的数值分析[J]. 青岛理工大学学报, 2006, 27(4): 34−37.HUANG Ming-li. Numerical studies of influence of heterogeneity on rock failure with pre-existing crack in uniaxial compression[J]. Journal of Qingdao Technological University,2006, 27(4): 34−37.

[5] 朱万成, 黄明利, 唐春安. 混凝土试件裂纹扩展及破坏过程的计算机模拟[J]. 辽宁工程技术大学学报: 自然科学版, 2000,19(3): 271−274.ZHU Wan-cheng, HUANG Ming-li, TANG Chun-an. Computer simulation on cracks propagation and failure process of concrete specimen[J]. Journal of Liaoning Technical University: Natural Science, 2000, 19(3): 271−274.

[6] 关宝树, 熊火耀, 翁汉民. 裂隙岩体强度的试验研究[J]. 西南交通大学学报, 1982, 17(1): 12−23.GUAN Bao-shu, XIONG Huo-yao, WENG Han-min. The experimental study of the strength of jointed rock mass[J].Journal of Southwest Jiaotong University, 1982, 17(1): 12−23.

[7] 张平. 裂隙介质静动应力条件下的破坏模式与局部化渐进破损模型研究[D]. 西安: 西安理工大学水利水电学院, 2004:10−30.ZHANG Ping. Research on the failure patterns and localized progressive failure models of the cracked media under static and dynamic stress condition[D]. Xi’an: Xi’an University of Technology. Institute of Geotechnical Engineering, 2004: 10−30.

[8] 唐春安, 刘红元, 秦四清, 等. 非均匀性对岩石介质中裂纹扩展模式的影响[J]. 地球物理学报, 2000, 43(1): 116−121.TANG Chun-an, LIU Hon-yuan, QIN Si-qing, et al. Influence of heterogeneity on crack propagation modes in brittle rock[J].Chinese Journal of Geophysics, 2000, 43(1): 116−121.

[9] 黎立云, 许凤光, 高峰, 等. 岩桥贯通机理的断裂力学分析[J].岩石力学与工程学报, 2005, 24(23): 4328−4334.LI Li-yun, XU Feng-guang, GAO Feng, et al. Fracture mechanics analysis of rock bridge failure mechanism[J]. Chinese Journal of Rock Mechanics and Engineering, 2005, 24(23):4328−4334.

[10] 王静, 师俊平. 有限板中裂纹应力强度因子的计算[J]. 岩石力学与工程学报, 2005, 24(6): 963−968.WANG Jing, SHI Jun-ping. Calculation of stress intensity factor for crack in a finite plate[J]. Chinese Journal of Rock Mechanics and Engineering, 2005, 24(6): 963−968.

[11] 黄明利, 唐春安, 梁正召. 岩石裂纹相互作用的应力场分析[J]. 东北大学学报: 自然科学版, 2001, 22(4): 446−449.HUANG Ming-li, TANG Chun-an, LIANG Zheng-zhao. Stress field analysis of interaction of rock cracks[J]. Journal of Northeastern University: Natural Science, 2001, 22(4): 446−449.

[12] Wong R H C, Chau K T. Crack coalescence in a rock-like material containing two cracks[J]. International Journal of Rock Mechanics and Mining Sciences, 1998, 35(2): 147−164.

[13] Bobet A, Einstein H H. Fracture coalescence in rock-type materials under uniaxial and biaxial compression[J].International Journal of Rock Mechanics and Mining Sciences,1998, 35(7): 863−888.

[14] Sahouryeh E, Dyskin A V, Germanovich L N. Crack growth under biaxial compression[J]. Engineering Fracture Mechanics,2002, 69(18): 2187−2198.

[15] Golshani A, Okui Y, Oda M, et al. A micromechanical model for brittle failure of rock and its relation to crack growth observed in triaxial compression tests of granite[J]. Mechanics of Materials,2006, 38(4): 287−303.

[16] 李强. 压缩作用下岩体裂纹起裂扩展规律及失稳特性的研究[D]. 大连: 大连理工大学岩土工程研究所, 2008: 10−35.LI Qiang. Study on laws of crack initiation, extension and failure in rock masses under compression[D]. Dalian: Dalian University of Technology. Institute of Geotechnical Engineering, 2008:10−35.

[17] 李银平, 杨春和. 裂纹几何特征对压剪复合断裂的影响分析[J]. 岩石力学与工程学报, 2006, 25(3): 462−466.LI Yin-ping, YANG Chun-he. Influence of geometric characteristics of pre-existing cracks on mixed mode fractures under compression-shear loading[J]. Chinese Journal of Rock Mechanics and Engineering, 2006, 25(3): 462−466.