基于ADL的浙江省总人口预测

冯霞

（杭州电子科技大学经贸学院，浙江杭州310000）

基于ADL的浙江省总人口预测

冯霞

（杭州电子科技大学经贸学院，浙江杭州310000）

通过对1994-2008年浙江省人口数据进行相关性分析，选取对总人口有显著影响的指标，进而对1990-2008年总人口差分序列及所选指标建立自回归分布滞后模型，并最终选出一个最优的模型，预测2009-2020年浙江省户籍总人口数。预测结果表明，至2020年，浙江省户籍总人口数将超过5000万，且依然呈现上升趋势。

自回归分布滞后模型；人口总量；人口预测

一、引言

浙江省历年户籍人口数据显示，2000年全省年末户籍总人口数为4501.22万人，比1990年的4234.91万人增加266.31万人，增长6.29%；2008年达4687.85万人；2010年达4747.95万人。可以预见，随着浙江省人口预期寿命逐渐增加和人口年龄结构逐步老化，全省人口问题势必加剧，并将对社会经济产生很大影响。

二、指标选取

因为浙江省人口迁移具有不规则性，未来的人口迁移控制很难准确预测，所以只建立封闭状态下的模型，即不考虑省际净迁移。

根据人口统计学的相关知识可知，一个地区的人口数受多重因素影响，包括人口内在因素、社会因素及经济因素等。因此，初步选取总人口y1t、65岁及以上老年人口（注：近年来国际上通常以65岁及以上人口称为老年人口，下文简称老年人口）y2t、男女性别比y3t、总和生育率y4t、死亡率y5t、平均预期寿命y6t6个人口指标。为了研究总人口指标与其他5个指标之间的关系，本文以1994-2008年浙江省户籍人口数据为样本数据，其中平均预期寿命以常住人口为统计口径，老年人口数为老龄化系数乘以同年户籍总人口数所得。利用SPSS软件，对上述6个指标作相关分析，得到各人口统计指标的相关系数及检验，见表1。

由检验结果可知，在显著性水平0.067下，老年人口、男女性别比、总和生育率及平均预期寿命与总人口的相关系数分别达到了0.887，-0.993，0.485，0.983，除死亡率外，皆通过显著性检验。这说明老年人口、男女性别比、总和生育率及平均预期寿命与总人口之间存在相关关系，且与客观事实相符。同时，由于死亡率与总人口的相关系数为0.083，其相伴概率为0.769，远大于显著性水平0.067，因而不能拒绝死亡率与总人口之间相关系数为0的原假设，即死亡率与总人口之间不存在相关关系——这也较为符合客观事实。根据浙江省1994-2008年户籍人口数据可知，户籍人口死亡率一直维持在6‰左右，而全省的户籍总人口依旧保持着持续增长，这表明样本期内总人口变化对死亡率基本上没有影响。

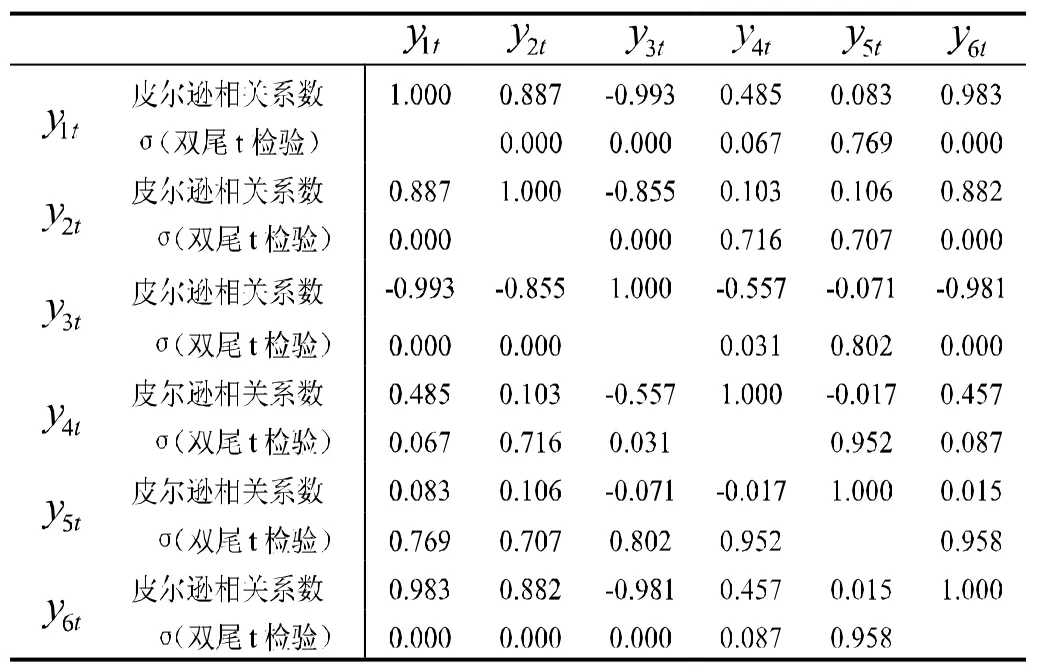
表1各人口统计指标的相关系数及检验

三、自回归分布滞后模型的建立

自回归分布滞后模型（Autoregressive distributed lag，简写为ADL），是指含有因变量yt的p阶滞后和k个额外预测因子的模型，其中包括第一个预测因子的q1阶滞后，第二个预测因子的q2阶滞后，以此类推。其一般形式：

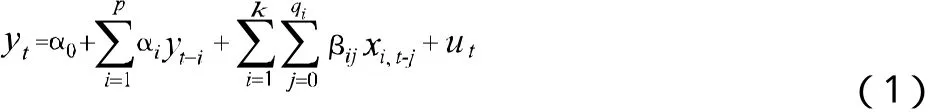
其中：（1）E（ut/Yt-1，Yt-2，…，X1t-1，X1t-2，…，Xkt-1，Xkt-2，…）=0。

（2）随机变量（Yt，X1t，…，Xkt）为平稳分布，随着j值的增大，（Yt，X1t，…，Xkt）与（Yt-j，X1t-j，…，Xkt-j）变成独立的。

（3）不存在完全多重共线性。

（4）X1t，…，Xkt和Yt具有非零的有限四阶矩。

由于社会环境、经济环境和人类自身发展等多方面的原因，各人口指标之间相互影响的效果，常常不是立即体现出来，而是有时间延滞性或持续作用，但会在以后一个或几个时期内逐步体现出来。因此，可选用自回归分布滞后模型进行建模并预测。此外，若在预测期间发生突发状况或重大灾难，导致人口状况发生突变，即使模型预测精度再高也可能无法准确预测，所以假设模型是在正常情况下进行预测。

自回归分布滞后模型主要是针对平稳时间序列的建模方法，时间序列的平稳性直接关系到模型的有效性。但是很多时间序列是非平稳的，因此在建立自回归分布滞后模型前，有必要对各序列进行平稳性检验。

（一）单位根检验

一般地说，如果非平稳时间序列yt经过d次差分达到平稳，则称其为d阶单整序列，记作I（d）。时间序列的平稳性是其数据计量分析有效性的基础，因此其平稳性检验具有重要意义。本文选采用ADF检验法，并根据赤池信息量（简记AIC）选择滞后期。以1990-2008年浙江省户籍人口数据为样本数据，运用Eviews软件作相应的单位根检验。

表2 ADF检验结果

检验结果显示，在0.11的显著性水平下，序列y1t、y2t、y3t、y4t都不是平稳序列，但是其差分序列▽y1t、▽y2t、▽y3t、▽y4t均为平稳序列，所以y1t、y2t、y3t、y4t为同阶单整，而序列y6t则是原序列平稳，与其他各人口序列不是同阶单整的。因此，在建立自回归分布滞后模型时，不选择平均预期寿命y6t及其滞后项为解释变量。

（二）自回归分布滞后模型的建立

由单位根检验可知，原序列y1t、y2t、y3t、y4t都是不平稳的，与自回归分布滞后模型的假设条件不符，而由于时间序列的差分序列与其本身包含许多一致的信息，所以差分与原变量之间常常可以相互转化。因此通过其差分序列、及建立ADL模型。

但是由于ADL模型即包含多个预测因子及其滞后期，也包含了被解释变量的滞后期。因此，ADL模型的参数估计有点困难，普通最小二乘回归也会遇到如下问题：

（1）没有先验准则确定滞后期长度；

（2）如果滞后期较长，将缺乏足够的自由度进行统计检验；

（3）模型存在多重共线性，具体表现为估计参数的标准差偏大，使t统计量不显著，但是总体上的F统计量的值却很高。

为使建立的人口预测模型有较高的估计精度，首先建立一个结构比较复杂的ADL模型，然后经过一些对参数的约束条件，去掉一些变量，并且反复进行建模和模型检验，最终得到一个具有良好性质的、表达简练的模型。虽然理论上可以采用OLS法估计各参数，但是考虑到多重共线性的存在，如果一味地设法剔除解释变量有可能引起模型的设定误差。因此，在剔除变量、删选模型的过程中，主要从模型的有效性及其预测精度着手。根据平均绝对百分误差（Mean Abs.Percent Error，简记为MAPE）和协变率（Covariance Proportion，简记为CP）来判断模型的预测精度，以AIC和SC来评价模型的优劣。一般认为，如果MAPE的值低于10，则预测精度较高，而CP则衡量了剩余的误差，当预测比较理想时，均方误差主要集中在CP上。此外，在所选的模型中，挑选AIC与SC相对较小的模型。

通过对数据的重复建模与检验，最后选定一个模型为

模型输出结果表明，其AIC与SC都相对较小，说明其拟合效果不错；此外MAPE小于10，CP更是达到了0.989，说明其具有较高的预测精度。分别对模型的残差项进行单位根检验及LM检验，确保所建模型的残差序列不存在有用信息没被提取，且残差序列的样本自相关系数应近似为0。检验结果见表3、表4。

表3残差序列单位根检验

表4残差序列LM检验

由表1可知，ADF检验统计量的值为-5.70，小于各不同显著性水平下的t统计量的临界值。因此，拒绝残差序列存在单位根的原假设，即残差序列是平稳的。这也表明该模型有效。表2中的检验结果显示，其相伴概率分别达到了0.88与0.72，即拒绝原假设所犯第一类错误的概率很大，这表明残差序列相互独立的概率很大，所以不能拒绝序列相互独立的原假设，说明残差序列的样本自相关系为0。

（三）模型的预测

1.控制变量的设定

根据客观实际，对总和生育率、男女性别比、老年人口作如下设定：

（1）总和生育率的设定。根据相关的人口统计学知识及浙江省目前基本稳定的低生育率水平，设定方案为，2009年总和生育率为1.35，2010年总和生育率为1.40，从2011年起每年上升0.02。

（2）男女性别比的设定。通过观察1990-2008年浙江省户籍人口的男女性别比数据可以发现，男女性别比指标一直呈下降趋势，但是每年的下降幅度不一，通过计算各年的下降幅度并计算出其均值为0.2。假定至2020年之前，男女性别比每年按0.2的速度下降。

（3）老年人口的设定。根据1990-2008年浙江省户籍老年人口数据，建立线性回归模型，预测未来老年人口的数量。假定老年人口y2t与时间t之间存在线性关系，建立的线性回归方程

第一排括号为系数检验的t值，第二排括号为t值的相伴概率。由模型输出结果可看出，模型（3）的显著性检验F值为139.20，相应的p值为0.000，表示无论置信度多小，关于模型各回归系数同时为0的假设都不成立，且模型调整后决定系数R2为0.885，说明模型的拟合效果不错。由括号中的数值可知，回归系数的t值分别为29.94与11.80，其相伴概率皆为0，这说明模型的系数对模型的影响是显著的。因此，用模型（3）预测2009-2022年浙江省老年人口数如表5所示。

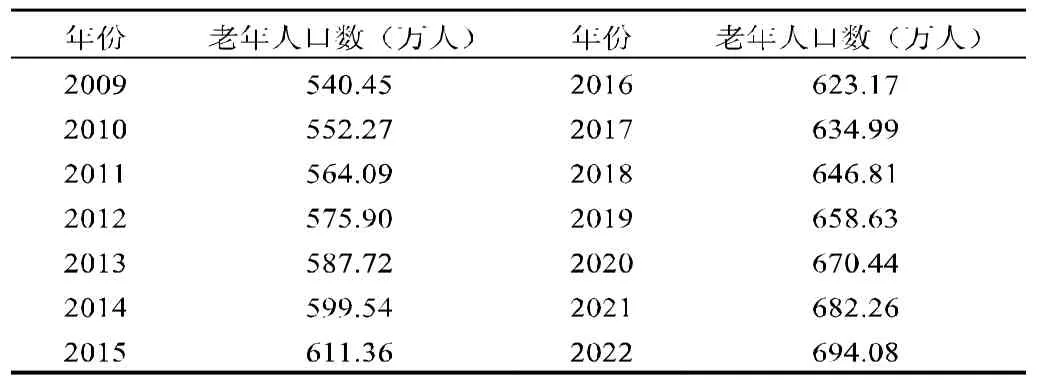
表5浙江省老年人口数预测值

2.总人口预测

根据65岁及以上老年人口数y2t、男女性别比y3t和总和生育率y4t的设定条件，以及模型（2）对浙江省户籍总人口增量进行预测，预测结果见表6。

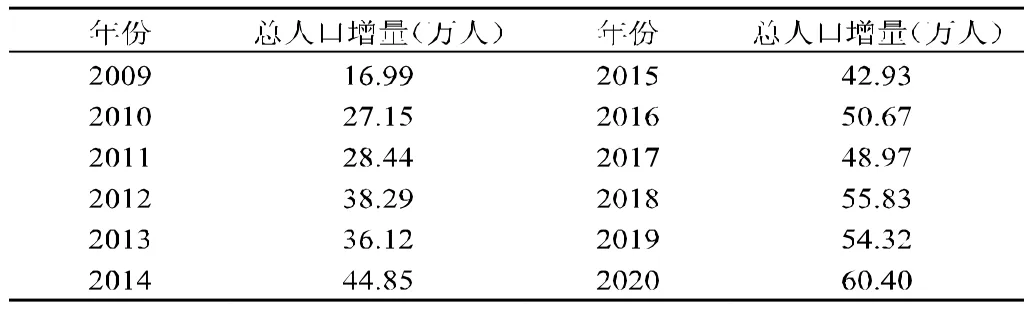
表6浙江省总人口增量预测值表

根据模型（2）总人口增量自回归分布滞后模型预测的浙江省户籍总人口增量预测值，再利用总人口数与总人口增量的关系式：y1t＝y1t-1＋▽y1t，得到2009-2020年浙江省户籍总人口数的预测值，具体结果见表7。

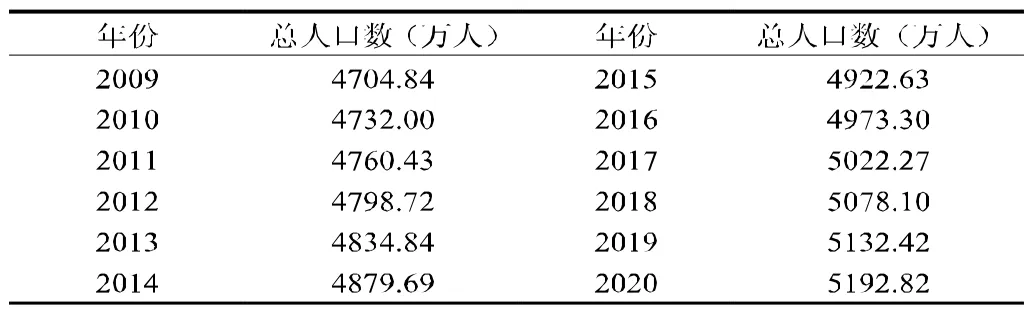
表7浙江省总人口数预测值表

3.结论

预测结果所示，浙江省总人口数在未来几年中还会呈上升趋势，至2020年户籍总人口数将达到5192.82万人，将增加487.98万人，增长10.37%，平均年增长率为8%。而这仅是在封闭的人口模型下的建模预测，若引入省际净迁入人口，情况会更复杂。因此，浙江省的人口问题必须及早关注，不仅应关注人口总量，同时还需关注人口年龄结构及人口质量问题。多维度地研究全省人口问题，有利于及时发现其急剧恶化的可能，主动应对，保障经济社会可持续和谐发展。

[1]安和平.中国人口预测的自回归分布滞后模型研究[J].统计与决策，2005（8）:4-7.

[2]田应福、王林.基于ADL模型的贵州人口时间序列分析[J].数理统计与管理，2009（7）:745-750.

[3]易丹辉.数据分析与Eviews应用[M].北京:中国统计出版社，2002.

[4]谢识予.计量经济学教程[M].上海：复旦大学出版社，2004.

[5]James H.Stock、Mark W.Watson（王庆石译）.经济计量学[M].大连:东北财经大学出版社,2005.

[6]张晓峒.应用数量经济学[M].北京：机械工业出版社，2009.

（责任编辑：施越霞）

book=1,ebook=1

10.3969/j.issn.1674-8905.2011.11.016