分层线性模型的最大后验估计

张 璇

分层线性模型的最大后验估计

张 璇

(中国人民大学统计学院,北京100084)

最大后验估计(MAPE)和最大似然估计(ML E)都是重要的参数点估计方法。在介绍一般分层线性模型(HLM)MAPE方法的基础上,给出这种方法的期望最大化算法(EM)的具体步骤,运用对数似然函数的二阶导数推导了MAPE估计的方差估计量。同时运用数据模拟比较了EM算法下的MAPE和ML E。对于固定效应的估计,两种方法得到的估计量是一致的。当组数较少时,EM计算的MAPE的方差协方差成分比ML E的更靠近真实值,而且MAPE的迭代次数明显小于ML E。

分层线性模型:最大后验估计:最大似然法:期望最大化算法

一、研究背景

自从Lindley和Smith提出分层线性模型[1]HLM(Hierarchical Linear Model)的概念以来, HLM在生物学、医学、社会学、教育学和经济管理方面的应用都得到了长足的发展。目前比较常用的分层线性模型的估计方法有最大似然法(ML)和完全贝叶斯法(Full Bayes)。理论研究表明大样本情况下,ML得到的参数估计是一致最优估计量, Bayes估计量是有偏的,但是Bayes估计考虑了所有辅助参数的不确定性,因此在样本较小的情况下能得到较ML更可靠的方差协方差的估计值。在计算方法上,ML运用期望最大化EM(Expectation Maximum)算法,Bayes运用MCMC算法,当分层线性模型形式较复杂时(如待定参数向量增多、层数增加等),MCMC运算并非能得到一个收敛的Markov链,而EM的算法简单快捷。

经典的频率学派和Bayes学派在统计推断方法上的争论由来已久,在参数估计时,如果对待估参数的先验信息一无所知,可以用频率学派的思想做参数估计;但是如果事先知道些许先验信息,Bayes估计可以提高参数估计的精度,减小参数估计的方差。最大后验估计方法运用了Bayes的分析理论,严格意义上说它的估计量并非是Bayes估计量,但是和极大似然相比,它考虑了待估参数的先验信息,是一种重要的估计方法。本文将介绍分层线性模型的最大后验估计方法以及EM算法的具体步骤。

二、分层线性模型的参数的最大后验估计

为了清楚地描述整个估计过程,运用一个简单的两层的分层模型。

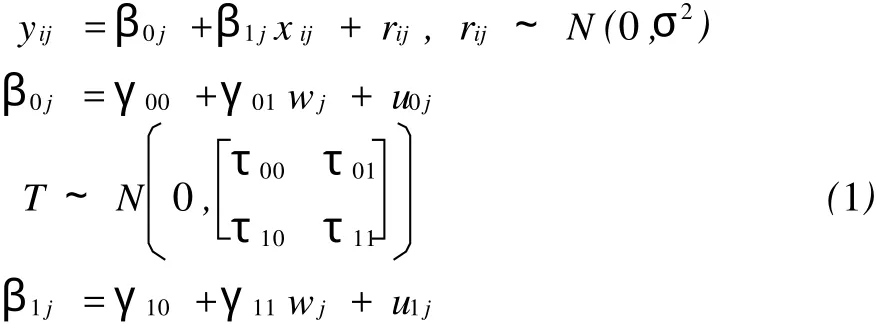
上述模型的矩阵形式是:

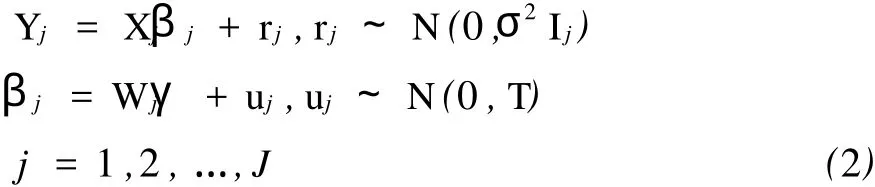
其中Yj是nj×1的因变量向量,Xj是nj×(Q+1)的自变量矩阵,(Q为层1模型自变量的个数,这里Q =1),βj是(Q+1)×1的待定参数向量,Ij是nj×nj的单位矩阵,rj是nj×1的随机误差向量;Wj是(Q+ 1)×F的自变量矩阵(这里F=4),γ是F×1的固定效应向量,uj是(Q+1)×1的层2误差向量或随机效应向量,T是(Q+1)×(Q+1)的方差协方差矩阵,并且通常假定模型中rj和uj是无关的,每层的自变量和该层的误差向量以及其它层的误差向量是无关的。

假设模型的参数向量θ=(γ,σ2,vech(T))①vech(T)表示将矩阵T的上三角元素按列拉直向量。,θ的先验联合密度函数为p(θ),则θ的后验密度函数为f(θ|Y)=p(θ)f(Y|θ)/f(Y),f(Y)是Y的边际密度函数和θ无关,所以f(θ|Y)∝p(θ)f(Y|θ)。由式(1)知rj和uj都服从正态分布,所以θ的对数对于p(θ),在没有太多信息的前提下,采用Jeffry先验密度函数[2],令p(θ)=C|T|1/2,其中C为常数,则对数后验密度

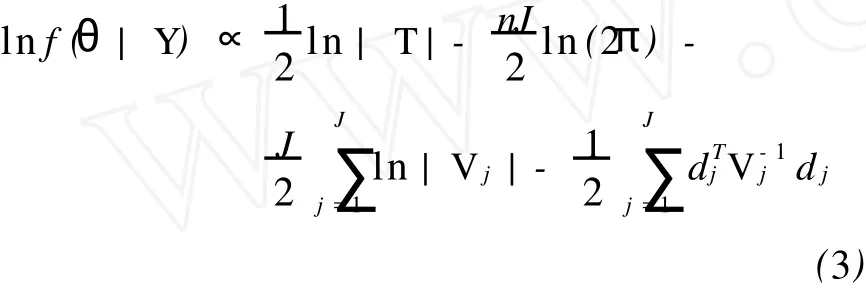
其中Vj=xjT+σ2In,dj=Yj-xjwjγ。为了简单起见,设定平衡的数据结构,每组样本的个数相等,均为n。

求lnf(θ|y)对γ,σ2,T的偏导数,计算中令φ =(τ00,τ10,τ11,σ2)T,根据Magnus或周杰对矩阵微积分的定义[3]89-133;[4]87-103,可以推出

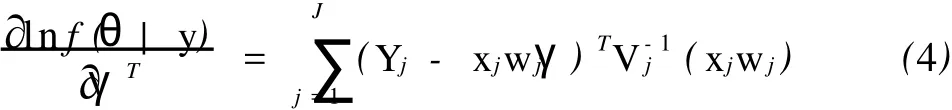
因为

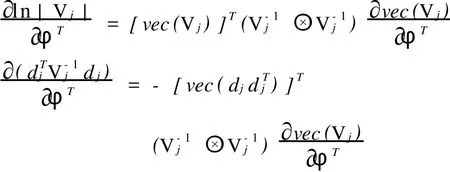
所以

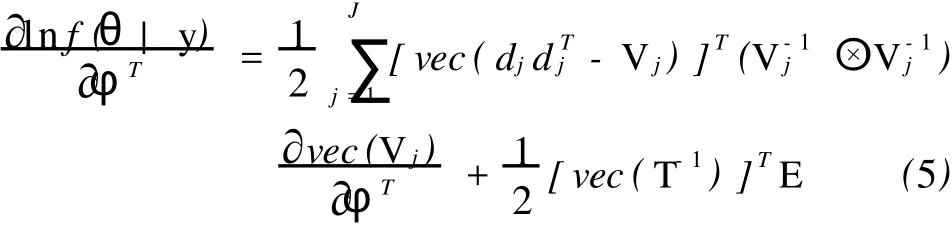
三、后验密度最大化的EM算法

在模型式(1)中,将βj看作缺失部分,θ和βj的联合后验条件密度函数为f(βj,θ|Yj)=p(θ)f1(Yj|βj,θ)f2(βj|θ)/f3(Y)∝p(θ)f1(Yj|βj,θ)f2(βj|θ),rj和uj都服从正态分布,所以θ和β1,β2,…,βN的联合后验密度函数为:

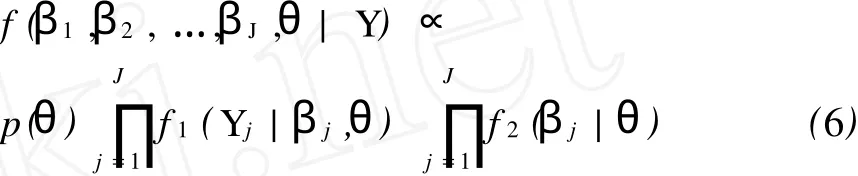
令p(θ)=C|T|1/2,其中C为常数,则对数后验密度为:

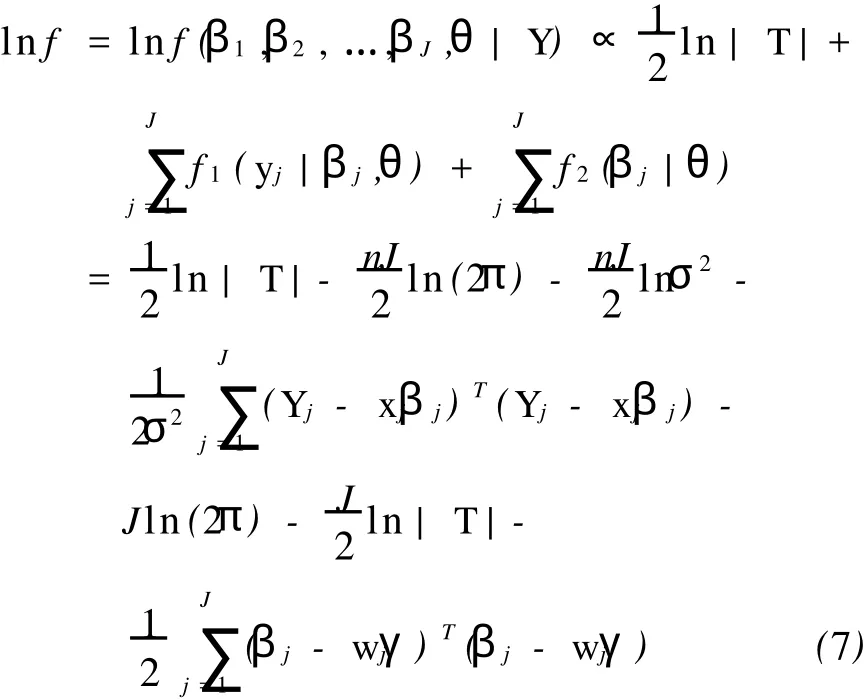
求lnf对γ,σ2,T的偏导数,并令其为零:

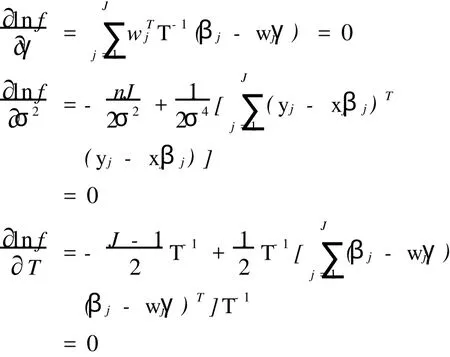
可以算出

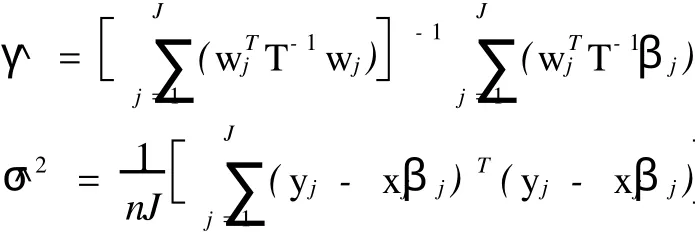
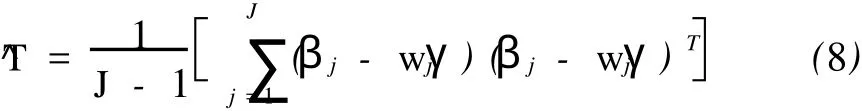
^γ,^σ2,^T的估计值均依赖βj,而βj是缺失数据,因此用EM算法实现计算。

EM算法能够处理带有缺失数据的模型估计[5],对于多峰分布,EM算法会收敛到观测数据似然函数的局部最大值;但是对于指数族分布,EM算法是相当好的,每一次迭代都会使观测变量的似然值增加,并达到全局最优[6]。在EM算法里,观测变量的似然函数的最大化可以转换为后验似然函数的最大化,EM算法可以修改用以计算最大后验估计,进行贝叶斯推断,在指数族分布下,能够和以往一样有效地收敛[7]64-85。

1.E步

为了找到E(βj|yj)和V ar(βj|yj),利用下面的多元正态分布。因为

其中

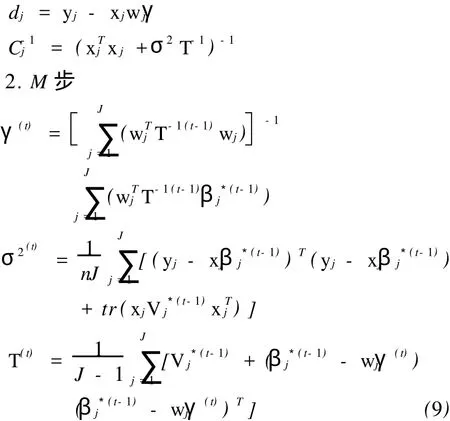
式(9)的具体推导过程如下:

首先由式(8),可以推出E(^γ|Yj),E(^σ2|Yj)和E(^T|Yj)。

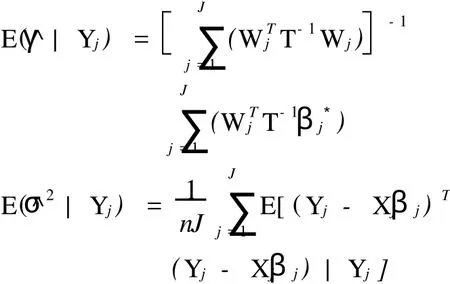
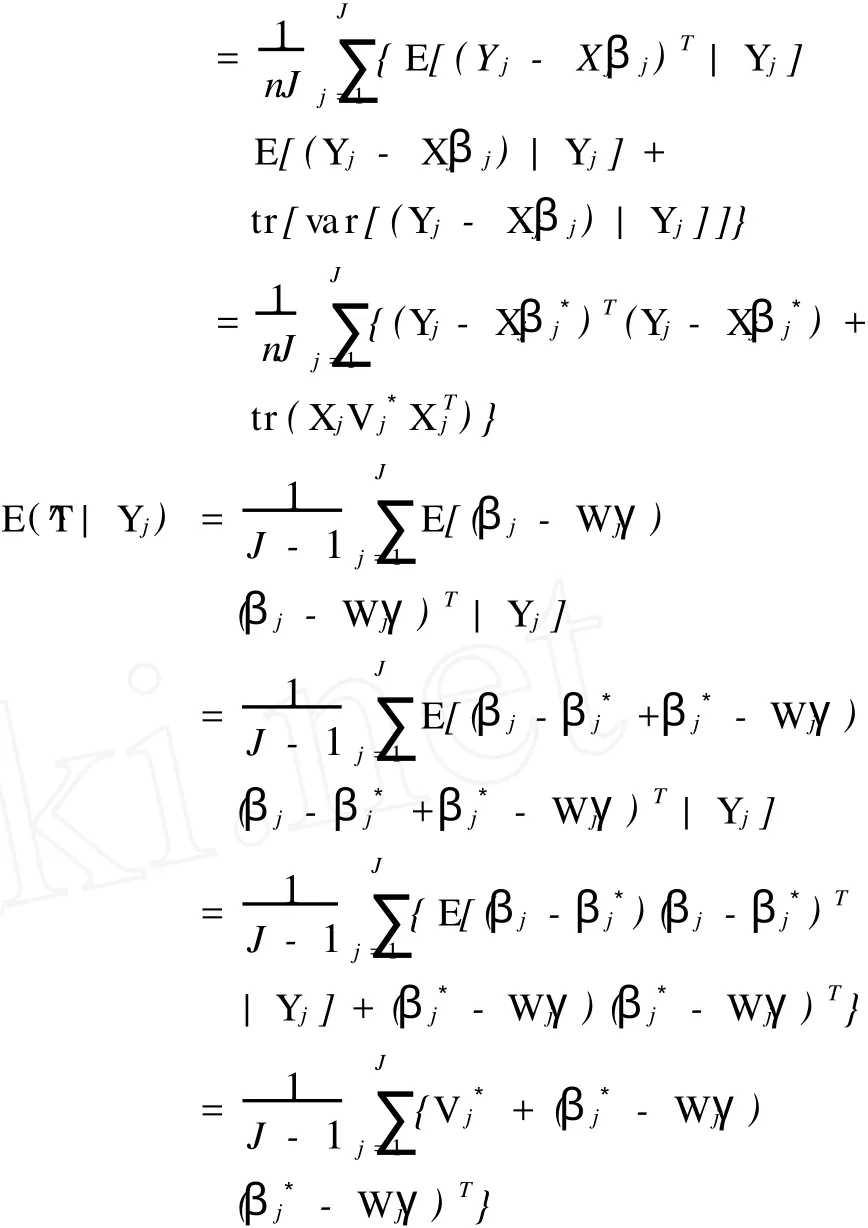
然后用E(γ^|Yj),E(σ^|Yj)和E(^T|Yj)分别替换γ^, σ^2和^T。

EM的计算过程为:①定初值γ(0),σ2(0),T(0);②将初值代入E步,计算;③再将的值代入M步,计算γ(1),σ2(1),T(1);④重复②～③,直至收敛。

四、参数估计值方差的计算

EM算法简单易行,但是参数估计的方差不能够直接从EM的迭代运算中产生,下面运用对数似然二阶导数,计算方差。将式(4)和式(5)分别再对r和φ求偏导,

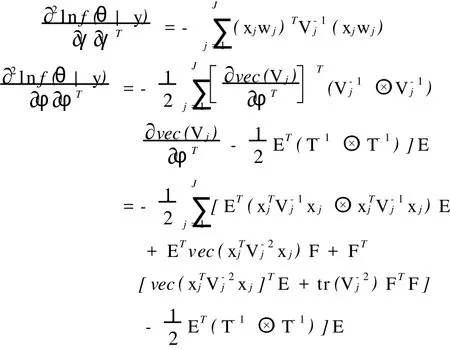
其中F=(0 0 0 1)。估计量的方差为

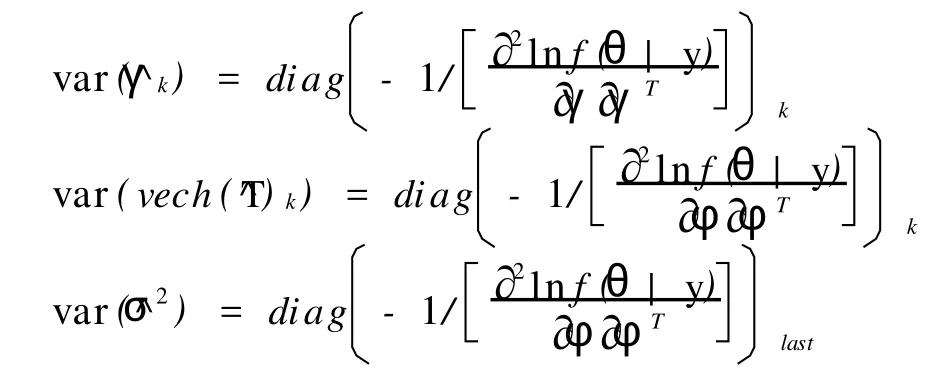
其中^γk表示γ的第k个元素,diag(A)k表示方阵A的对角线上第k个元素,diag(A)last表示方阵A的对角线上最后一个元素。

五、数据模拟

StephenW.Raudenbush和AnthonyS. Bryk[8]428-429给出了两层HLM的MLE的具体步骤,虽然REML和Bayes估计在小样本时改进了模型的估计,但MLE的估计量仍可以作为一个参照的标准估计。下面将从样本量的变化和初值设定的变化来对最大后验估计方法进行数据模拟,并将结果和MLE的估计进行比较。

(一)模拟样本的产生

假定模型式(1)的一个较简单形式。从N(0,1)中随机生成x和w的样本,样本量分别为n3N(n =30,50,100为组内个体数,N=30,50为组数);σ设为0.7,从N(0,0.72)中随机生成r的样本;为了计算方便,令τ10=0,τ11=τ00=0.3,随机生成u0和u1的样本;令γ00=1,γ10=γ01=γ11=0.3,由模型(1)得到y的样本值。以下表格数据均为500次模拟计算的平均值。

(二)MAPE估计结果以及和MLE的比较

考虑到样本量的大小会影响估计的结果,本研究用不同的组数30,50,100和个体数30,50的不同组合进行数据模拟,每个样本量下模拟500次。将MAPE和MLE估计中的迭代的初值都设定为1),结果参见表1～3。

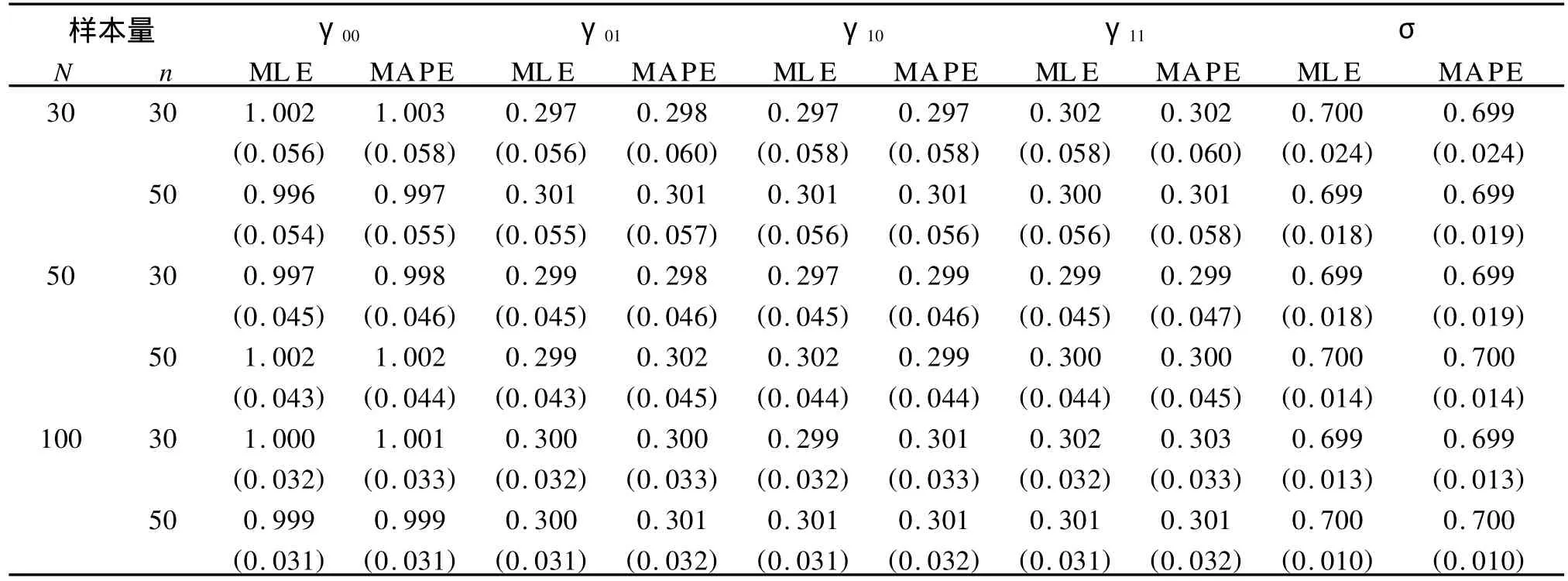
表1 固定效应和方差σ的MAPE和ML E及其方差估计值的比较表

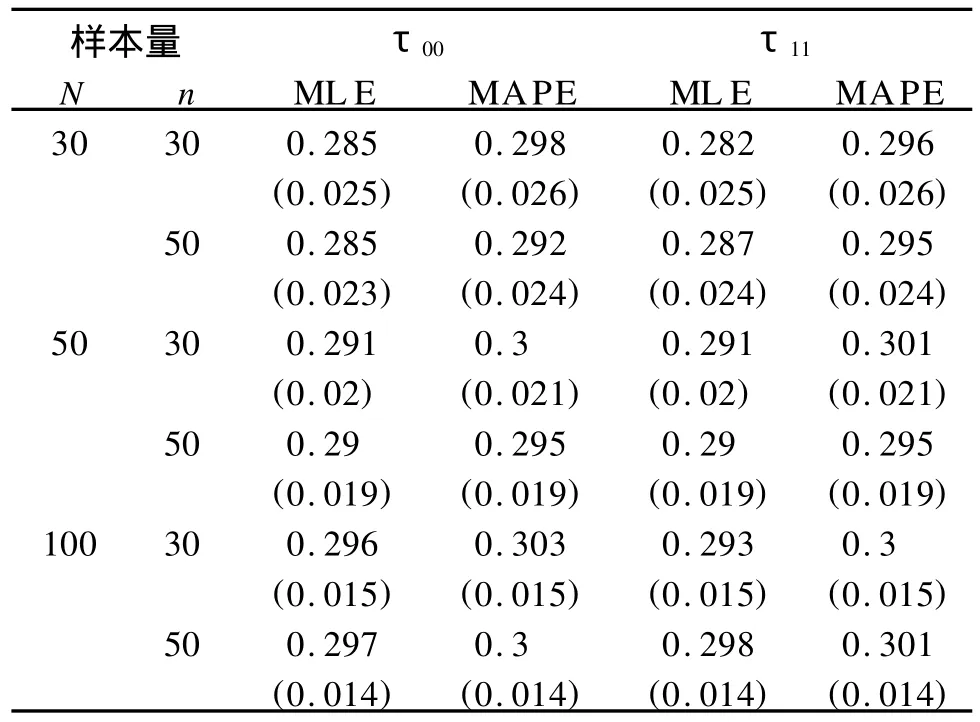
表2 方差协方差成分的MAPE和ML E及其方差估计值的比较表

表1列出了MAPE和MLE两种估计方法下,固定效应参数γ00至γ11以及σ在不同样本量下的估计值和标准差(表中用括号表示)。可以清楚地看到两种估计方法对固定效应的系数和方差σ2的估计值在不同的样本量下是一致的,并且500次模拟的平均值和真实值的绝对差都在0.006以内;MAPE估计量的标准差稍大一点,两者的绝对差在0.004以内,差距很小。

表2描述了在不同样本量下,两种方法对方差协方差成分τ00,τ11的估计情况。在(N,n)=(30, 30)时,τ00,τ11的MLE估计值与真实值绝对差为01015和0.013,MAPE为0.008和0.005,在(N,n) =(30,50)时,τ00,τ11的ML E估计值与真实值绝对差为0.011和0.014,MAPE为0.003和0.006,当组数和总的样本数增加时ML E的绝对差也能减小到0.01以下。这说明组数少、总样本量小的时候,τ00, τ11的MAPE的估计比MLE的估计更接近真实值,当组数增加,总样本量增加时τ00,τ11的估计是一致的,并且都靠近真实值。另外,与固定效应的估计一样,估计量方差的MAPE稍大一点,但也随着样本量的增加而趋于相同。

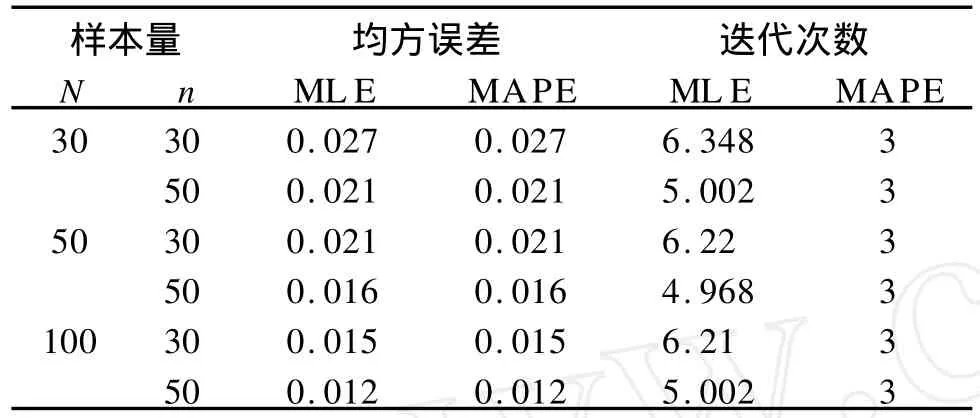
表3 MAPE和ML E的均方误差和迭代次数的比较表

表3比较了两种方法估计的均方误(MSE)和计算的迭代次数。在相同的样本的情况下,MAPE和ML E的MSE是一致的,并且模拟显示它们都随样本的增加而减少。对迭代次数而言,ML E的迭代次数明显高于MAPE,而且MAPE的迭代次数不受样本量的影响,收敛得很快。

下面将减小样本量继续进行模拟比较,样本量组数N和组内个体数n分别为:N为5,10和20;n为10,20。比较结果见表4～5。表4描述的模拟结果和表2类似。可以清楚地看到当组数减小到5,组内个体数减小到10时,τ00的MLE的估计值为0.18,而MAPE为0.293,和真值0.3相比,MAPE的估计值比ML E更靠近真实值。随着组数的增加,当组数超过50时,两种估计值都趋于真实值。

随着组数的减少,MLE的迭代次数明显增加。表5显示出小样本下的两种方法的模拟的MSE值和迭代次数。两种估计方法的MSE仍是一致的,但是MAPE估计的迭代次数明显低于MLE的迭代次数。

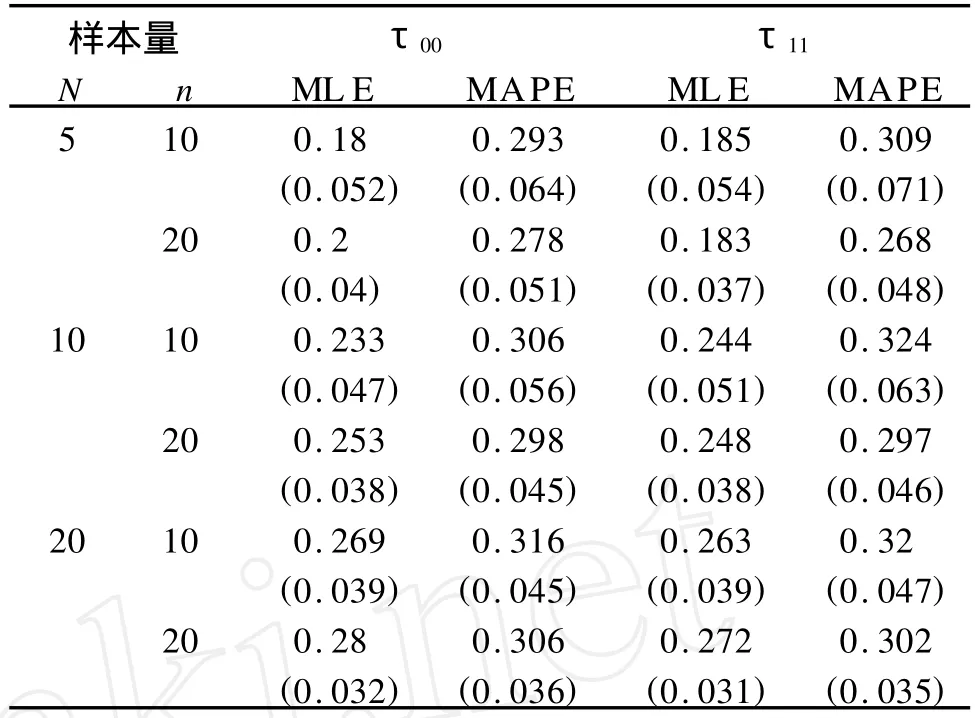
表4 更小样本下方差协方差成分的MAPE和ML E及其方差估计值的比较表

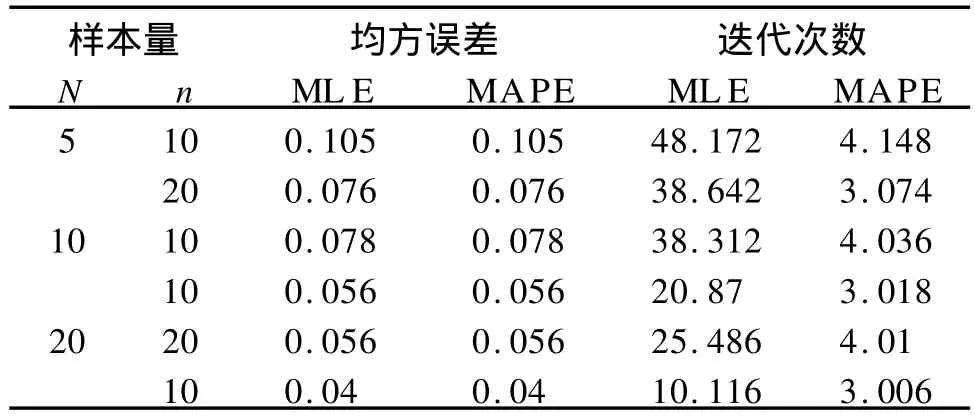
表5 更小样本下MAPE和ML E的均方误差和迭代次数的比较表

六、结 论

本文推导出一个适合分层线性模型进行最大后验估计的EM算法,并利用似然函数的二阶导数推导出参数估计的方差估计值。在数据模拟中,将新的EM算法的结果同极大似然估计的EM算法的结果进行比较,得出的结论是:1.对于固定效应r和方差σ估计值,两种方法是完全一致的。2.组数较少,样本量较小时,EM计算的MAPE的方差协方差成分的估计比用EM计算的ML E的估计更靠近真实值。3.EM计算MAPE迭代次数小于ML E;尤其当样本量较小时,两者之间的差距很明显。

[1] Lindley D V,Smith A F M.Bayes Estimates for Linear Model[J].Journal of the Royal Statistical Society,Series B,1972,34.

[2] Jeffreys H.An Invariant Form for the Prior Probability in Estimation Problems[J].Proceedings of the Royal Society of London,Series A,Mathematical and Physical Sciences,1946,186.

[3] Magnus J R,Neudecker H.Matrix Differential Calculus with Applications in Statistics and Econometrics[M].New York:John Wiley,1988.

[4] 周杰.矩阵分析及应用[M].成都:四川大学出版社,2008.

[5] Dempster A P,Laird N M,Rubin D B.Maximum Likelihood from Incomplete Data Via the EM Algorithm[J].Journal of the Royal Statistical Society,Series B,1977,39.

[6] Wu C F,Jeff.On the Convergence Properties of the EM Algorithm[J].Annals of Statistics,1983,11.

[7] Tanner M A.Tools for Statistical Inference[M].Heidelberg:Springer-Verlag,1996.

[8] Bryk A S,Raudenbush S W.Hierarchical Linear Models[M].Newbury Park,CA:Sage,1992.

Maximum a Posteriori Estimate of Hierarchical Linear Model

ZHANG Xuan
(School of Statistics,Renmin University of China,Beijing 100084,China)

Maximum a posteriori(MAP)estimation is an important method in statistical estimation. This research develops MAP estimation for Hierarchical Linear Model(HLM),and gives a detailed process of estimation and computational program.The expectation maximum(EM)algorithm was adapted to the concrete calculation,and the second derivatives of log likelihood function help us to obtain the esti2 mators of variance and covariance components in this model according to asymptotic distribution theory of maximum likelihood estimator.At last,we compare the results of MAP estimate to the general maximum likelihood(ML)estimate,noting that EM algorithm is exploited into the two different estimates.Simula2 tion shows that the estimators of fixed effects using the two methods are almost consistent,but the MAP estimators of variance and covariance components are closer to real values than the ML estimate counter2 part when the group size is small,at the same time,the iterations needed in MAP estimate are obviously less than those in ML estimate.

hierarchical linear model;maximum a posteriori estimate;maximum likelihood estimate; expectation maximum algorithm

F224.7

A

1007-3116(2011)01-0010-06

(责任编辑:马 慧)

2010-08-29

张 璇,女,湖南湘潭人,讲师,博士生,研究方向:统计模型及其计算、计量经济学。