基于遗传算法的公司生产销售方案制定

安哲成，于广瀛

(1.大连理工大学信息与通信工程学院，辽宁大连116024;2.大连理工大学能源与动力学院，辽宁大连116024)

企业是从事生产、流通、服务等经济活动，以生产或服务满足社会需要，实行自主经营、独立核算、依法设立的一种盈利性的经济组织。作为社会活动的重要参与者，企业承担生产产品并将其推向市场、进行销售的社会责任。企业生产的产品主要通过营销部进行销售［1］。

对于生产方案，在满足已签约的销售合同量的基础上，对意向签约量有选择地安排生产。对于销售方案，企业的产品销售共有三种途径:第一，企业组织安排生产，完成已签约的销售合同;第二，企业希望营销部门与意向签约的客户签订正式销售合同;第三，企业希望营销部门销售更多产品(计划外)。

关于利润计算，对于所签约的销售合同和意向签约量(计划内)，企业根据销售量向营销部发放经费(包括工资以及宣传费用等);对于计划外销售的产品，实行承包制，营销部向企业缴纳利润。产品的生产费用由企业承担，与销售有关的费用(如产品的宣传费用等)由营销部承担。

在上述问题背景下，企业产品生产销售方案的制定直接决定着企业及其营销部的利润收益。因此，优化企业的产品生产销售方案，使企业及营销部获得最大收益期望，具有重大的现实意义。

1 问题分析

在企业运营过程中，企业决策部门根据自身生产能力、已签约订单数量、意向签约订单数量和计划外销售量的可能情况制定生产方案。在这个问题中，意向签约订单数量和计划外销售量为满足一定分布的随机变量，在单次试验中其具体取值不可预知，并且产品的生产先于意向订单及计划外订单的签约和这部分产品的销售过程，也就是说，产品的生产方案不能够根据这些随机变量的具体取值而调整。

对于确定的生产和销售方案，利润等指标是关于意向订单签约量和计划外订单签约量等随机变量的函数，即利润等指标也是随机变量。为使确定的生产方案应对不确定的意向签约订单和计划外订单的实际签约情况，使用各种指标的数学期望作为目标函数并对其进行优化［2－3］。数学期望本身是随机变量的取值以其出现概率为权重的加权平均数，在指标函数的各随机自变量的已知分布函数的情况下，数学期望能够精确全面地反映各种可能发生的实际情况，为生产方案的制定提供依据。

2 模型建立

2.1 利润计算

设企业共生产 n种产品，用 xi(i=1，2，...，n)表示第i种产品的生产量;用yi表示第i种产品的订购量;用zi表示第i种产品的销售量，z1i表示计划内订单的销售量，z2i表示意向签约订单的销售量，z3i表示计划外的销售量。设pi(z3i)为营销部向企业缴纳的关于第i种产品的计划外销售量z3i的利润函数;ci(xi)为第 i种产品的生产成本关于第i种产品产量xi的函数;si(zi)为第i种产品的销售额关于其销售量zi的函数;di(z1i+z2i)为企业下放营销部的针对计划内产品的运营经费关于第i种产品中计划内销售量z1i+z2i的函数;ui(zi)为第i种产品的宣传费用关于i种产品销售量zi的函数。

公司的利润为公司的总收益和支出之差。公司的总收益为计划内销售额和营销部计划外营业额上缴的金额之和，支出为生产总成本和根据计划内销售量向营销部发放的经费。营销部的利润等于营销部的收益减去营销部的支出，其中:营销部的总收益为计划外订单的销售额与公司派发的计划内经费之和;营销部的支出包括计划外订单的宣传经费和上缴利润。

对于不同的订单，用z1ij表示第i种商品第j份计划内订单的销售量，N1i表示第i种商品的计划内订单总数;用z2ij表示第i种商品第j份实际签约的意向订单的销售量，N2i表示第i种商品的实际签约意向订单总数，则全部的n种商品的计划内销售额Sc等于各种商品的已签约订单销售额与意向签约订单的实际销售额之和:

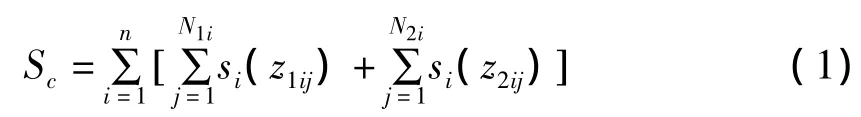
设计划外商品的销售量为z3i，营销部销售计划外产品后上交公司的利润为P，则有

设所有产品的生产成本为C，则有

设计划内产品下放营销部的运营经费为D，则有

式中:z1i表示第i种产品的已签约订单实际销售总量;z2i表示该产品的意向签约订单的实际销售总量，即

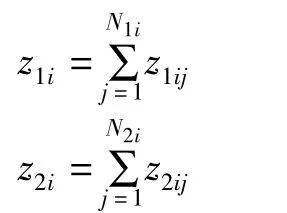
所以，公司的总利润可用下式表示

同理，营销部的总利润为

其中，Ss为营销部获得的计划外订单销售额，假设所有的计划外销量均来自于同一个订单，故有

设所有产品的宣传费用为U，有

2.2 约束条件

设y1i为各种产品的签约合同量，各种产品的意向签约量为y2i，计划外订购量为y3i。各种产品的签约合同销售量z1i、意向合同销售量z2i、计划外销售量z3i的取值需要满足销售量不超过订购量的约束条件

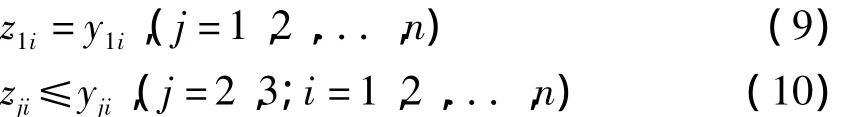
各种产品的产量和各种产品销售量的关系应该满足如下关系

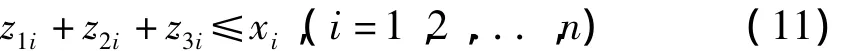
并且各种产品的产量应符合公司的生产能力，设公司生产能力的约束条件为

将满足式(9)、(10)、(11)、(12)的(x1，x2，...，xn)的取值集合设为X，则集合X为优化问题的约束条件。

2.3 优化模型

2.3.1 公司利润极大化值

在设计产品销售分配方案时，销售策略只针对超出已订购订单生产的产品，给出销售给意向订单和计划外订单的分配方案。制定销售方案需要考虑订货量相同的订单、销售给意向订单及计划外订单时公司和营销部所获得的利润。

通过分析两个部门的利润和不同订单的资金分配关系，发现当产品出售给意向客户时，企业拿到该订单的销售额，同时拿出一部分资金分给营销部当做经费;当产品出售给计划外客户时，营销部获得该订单的销售额，同时销售部拿出一部分资金作为上缴利润交给企业。可将两个部门的收入关系简化为:当产品出售给意向订单时，销售额中取出一部分作为经费分给营销部，其余资金均归企业所有;在销售给计划外客户时，销售额的一部分作为上缴利润分给企业，剩下的资金归营销部所有。根据这种销售额分配政策，得到了企业出售某一批商品给意向订单和计划外订单时的利润情况，如图1所示。

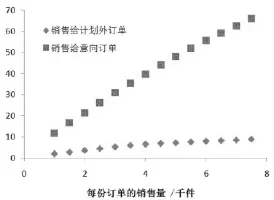
图1 产品销售给不同类型订单时公司获得的利润

从图1中可看出，使公司自身获得最大利润，应在满足签约订单的基础上，优先考虑计划内的最大订单。即:

1)签约订单为题目已知条件，即z1、S1已知;

2)满足签约订单后，将剩下的x－y1件产品优先售予意向订单;若仍有剩余则考虑计划外订单，可得到z2，进而可得S2;

3)由2)可求得 z3，z3=x－ z1－ z2，于是求得P;

4)同样，在已知 x、z后，可求 C、D;

5)具体求解公司利润的公式如下:以企业利润最大为条件的营销方案为

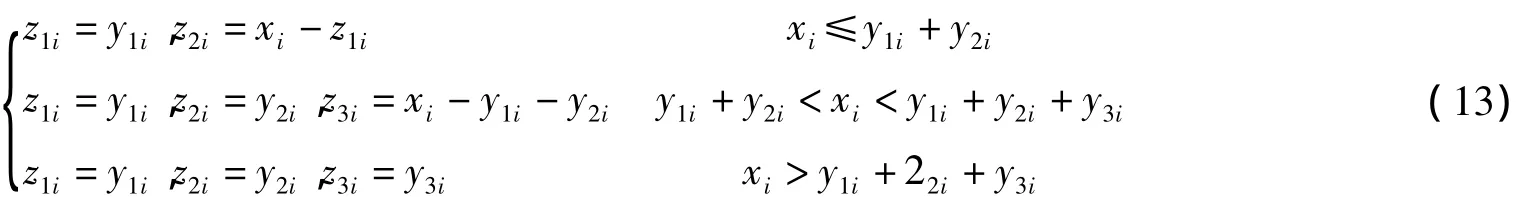
式(13)即为在确定生产方案的情况下，根据xi和y1i、y2i、y3i制定的销售方案。其中，z2i有可能不满足所有的实际意向订单。假设只提供某份订单的一部分需求，不能满足全部实际意向订单的意向签约产品销售量z2i将被用来优先随机满足一些订单，零余部分用来满足部分随机的某份订单的需求。这里将每份订单大小造成的销售额的偏差忽略不计。对于计划外销售量z3i，也使用此方法进行处理。

将式(13)带入式(5)可得公司最大利润Qc。

由2.2 的分析可知，Qc是关于 x1，x2，...，xn的函数，同时也是关于随机变量x2ij、y3i的随机变量函数，取Qc的数学期望E(Qc)作为目标函数，故此时的生产方案优化模型为

2.3.2 营销部利润极大化值收益的分析和简化，可得到相同数量产品出售给意向订单和计划外订单时营销部的收益。

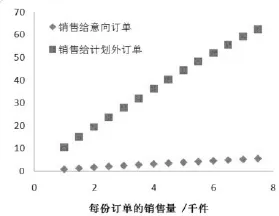
图2 产品销售给不同类型订单时营销部获得的利润

由图2可知，营销部争取更多的计划外订单才能获得更多的利润。即将满足已签约订单剩余的x－z1个产品优先供给计划外订单，仍有剩余产品时再供给意向订单。

按照x－z1与y3i的大小关系，可得表达式如下:

根据2.2的销售方案中对公司和营销部获得

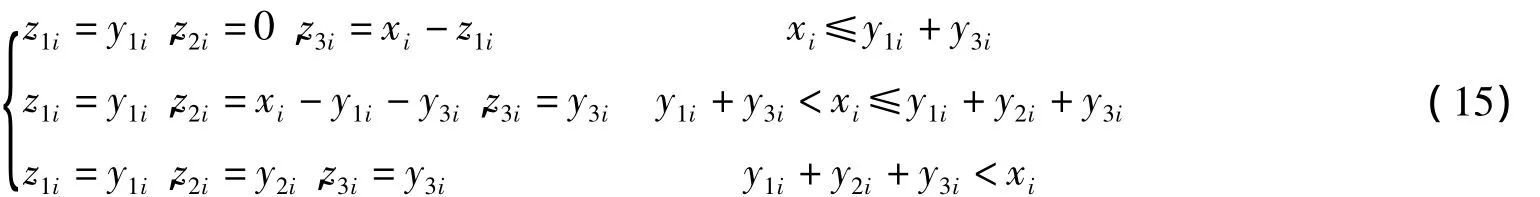
将式(15)代入式(6)可得营销部最大化利润Qs。

与上一模型相似，此模型中待优化变量Qs与产品的生产量xi有关。通过优化可求得营销部的最大受益及此时的生产量方案。

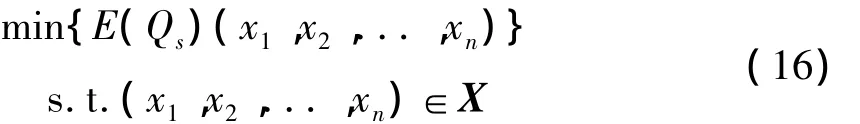
2.3.3 兼顾公司和营销部的利益

从2.3.1和2.3.2的分析可知，优先接收意向订单，公司可以获得很多利润，而营销部获得的收益较少;优先接收计划外订单，则公司收入少，营销部获得利润较多。所以如何分配两类订单的产品销售数量直接影响企业与营销部的收益平衡问题。在此引入分配比重的调整系数k，k∈(0，+∞)。当第i种商品的生产量为xi，已签约订购量为y1i，意向订购量为y2i，计划外订购量为y3i时，就有xi－y1i的产品可售给意向订单和计划外订单，调整系数k则有的产品销售给意向订单，剩下)的产品销售给计划外订单。k越大供给意向订单的产品越多。通过建立评价指标作为目标函数对生产量和分配比重进行优化。评价体系既要使企业和营销部的利润尽可能大还要兼顾双方的利润分配，所以评价指标包含公司和营销部总利润评价指标及公平性评价指标。

要求企业和营销部的收益和尽可能大，二者利润加和后进行归一化得到利润评价指标为

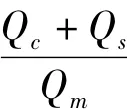
式中:Qc为公司的利润;Qs为营销部的利润;Qm为企业和营销部的理论总收益的最大值。Qm用于对实际的Qc和Qs之和进行归一化处理，实际计算中Qc和Qs之和不一定能真正达到Qm。这里的Qm为前两问中优化得到的企业和营销部的最大利润之和。

在考虑公平性时，需要权衡企业与营销部的利润比例。设企业与营销部的利润比为1∶δ时为最佳的利润分配方案，归一化后得到利润分配公平性的评价指标。

综合考虑总最大收益和公平性指标，将两者的权重设为ω1和ω2，得到最终的评价指标函数G。

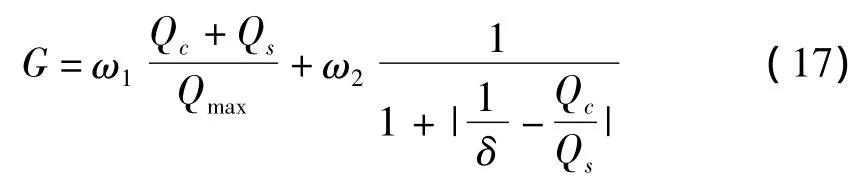
同样对指标函数G求关于各随机变量的数学期望，得到E(G)。G以产品生产数量xi和调整系数ki为自变量的函数，优化后可得最优产品生产和销售方案。

3 模型求解

3.1 蒙特卡洛方法求数学期望的近似解

以上模型均以含有随机变量的指标函数的数学期望作为目标函数。由于大多数优化算法需要反复计算目标函数的函数值，因而如何高效地求解这些指标函数的数学期望成为解决此问题的关键。假设每个客户订购每种商品的数量是相互独立的随机变量，故各指标函数均包含大量的相互独立的随机变量。

为了优化指标函数数学期望计算的时间复杂度，使用蒙特卡洛算法来近似计算指标函数的数学期望［4］。利用计算机随机生成相互独立的满足各随机变量分布的随机数，最为各随机变量的取值来模拟订单情况，计算出此时的指标函数值。反复多次按此方法计算指标函数的函数值，最后计算平均结果，作为指标函数的数学期望的近似结果。

经检验，计算1000次指标函数的值取平均数得到的近似数学期望具有较好的稳定性，并且在普通PC机上程序运行的时间小于20毫秒，可满足计算需求。

3.2 遗传算法优化模型

2.3 中各优化模型的约束条件为线性的，目标函数是以随机变量为分界点的分段函数，需通过蒙特卡洛算法计算其近似结果。同时，计算目标函数需要用到的销售额、生产成本等函数是通过表格的形式给出，没有解析表达式。综上所述，优化模型中的目标函数具有高度非线性化、非连续等特点，难以使用求解线性优化模型的单纯型法或求解连续可微模型的牛顿法来进行优化求解［5］。本文利用遗传算法来求解此优化模型［6－7］。

将生产量作为个体，将目标函数即指标函数的数学期望作为适应度指标。首先随机生成若干个个体作为初始种群，每个个体对应的基因包含每种产品计划生产量或者每种产品的分配比重调整系数，通过计算每个目标基因的适应度，使适应度较高的个体更容易被保留下来，产生后代。亲代所产生的子代由其亲代的基因通过交叉组合和变异产生，新的个体组成下一代继续进行选择。这样经过种群的演化和选择可使整个种群向着适应度最高的方向进化，最终得出适应度最大即获得收益最高的个体种群［8］。此时种群中每个个体的基因基本相同，对应着收益最大时的计划生产量和分配比重调整系数。

使用MATLAB R2009a中的gatool工具箱实现此算法，设定初始种群数量为20个个体。通过多次迭代目标函数，选择最后的结果，最为最终的近似最优解。

4 计算实例

将某家电生产企业的数据带入模型，进行求解，得到如图3、4、5的结果。从图中看到，公司的最大利润收敛于1687.92万元，营销部的最大利润收敛于472.41万元，综合评价指标收敛于0.84(注:企业数据来源于2010年东北三省数学建模联赛A题附表)。

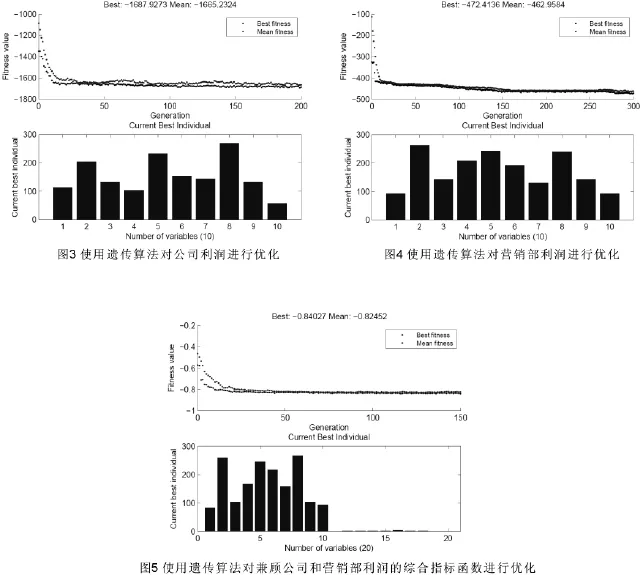
根据图1、图2、图3得到最佳生产量方案，如表1、表2、表3所示。

表1 公司利润最大时每种产品的最优计划产量 千件

表2 营销部利润最大时每种产品的最优计划产量 千件

表3 兼顾公司和营销部收益时每种产品的最优计划产量及分配方案 千件

5 结论

本文针对企业生产销售方案制定问题，分析了产品生产数量、客户订单和产品销售量三者之间的关系，给出了公司和营销部的利润计算公式。在平衡公司和营销部二者利益时，引入了分配比重的调整系数。通过建立综合评价指标作为目标函数对生产量和分配比重两个自变量进行优化，得到二者的最优化方案并且在利润最大的同时，兼顾公平。在模型求解的过程中，蒙特卡洛算法的应用降低了求解多维随机变量数学希望的时间复杂度。遗传算法的应用体现了其求解高度非线性化目标函数及约束条件下的运筹模型时的强大优势。计算实例表明模型求解的结果有较好的收敛性和近似性。

［1］何晏.成本、数量、利润分析法在企业管理中的应用［J］.商业经济与管理，1987，(1):49 －54.

［2］姜启源，谢金星，叶俊.数学模型［M］.北京:高等教育出版社，2004.

［3］陈涛.目标规划在制定企业生产计划中的应用探讨［J］.经济师，2011，(3):259 －261.

［4］尹增谦，管景峰，张晓宏，等.蒙特卡罗方法及应用［J］.物理与工程，2002，3(12):45 －49.

［5］郭科，陈聆，魏友华.最优化方法及其应用［M］.北京:高等教育出版社，2007.

［6］周明，孙树栋.遗传算法原理及其应用［M］.北京:国防工业出版社，2002.

［7］葛继科，邱玉辉，吴春明，等.遗传算法研究综述［J］.计算机应用研究，2008，(10):2911 －2916.

［8］徐宗本，李国.解全局优化问题的仿生类算法(I)－模拟进化算法［J］.运筹学学报，1995，(2):1 －13.