基于灰色关联的季不均衡系数的分析方法与应用

徐 飞，周步祥，林 楠

(1.四川大学电气信息学院，四川 成都 610065;2.四川电力职业技术学院，四川 成都 610072)

0 引言

在年负荷特性中，季不均衡系数(又称季不均衡率ρ)［1］与年负荷曲线的波动性和年最大负荷出现的时间有关，而影响年负荷曲线形状的主要因素是负荷的季节变化、用电设备的大修及负荷在年内的增长。

文献［2］-［7］分别对广州、汕头、固原、南京、上海等地的负荷特性进行了详细的分析和说明，指出了各个地方负荷特性的影响因素和负荷特性的发展趋势，符合当地的实际情况，但是，没有定量地说明负荷特性的主要影响因素，并且分析过程不易推广到其他地区或城市。

这里引入了灰色关联度分析［10］理论用来定量分析各影响因素的权重，并在此基础上预测该地区未来季不均衡系数的发展趋势。通过实际应用，该算法能够很好地切合实际情况，并且计算过程比较容易推广。

1 季不均衡系数分析

1.1 影响因素

影响季不均衡系数的主要因素可以总结为3个方面。

(1)经济结构

经济结构因素包括:GDP(亿元)、GDP增长率(%)、第一产业GDP比重(%)、第二产业GDP比重(%)和第三产业GDP比重(%)等。

如第二产业比重占主导地位，年负荷特性曲线波动较平缓，季不均衡系数较大，相应的最大负荷利用小时数也较大;如第三产业比重占主导地位，则相反，年负荷特性曲线波动较剧烈，季不均衡系数较小，相应的最大负荷利用小时数也较小。

(2)用电结构

用电结构因素包括:第一产业用电量比重(%)、第二产业用电量比重(%)、第三产业用电量比重(%)、居民生活用电量比重(%)等。

如第二产业用电量比重占主导地位，年负荷特性曲线波动较平缓，季不均衡系数较大，相应的最大负荷利用小时数也较大;如第三产业用电量和居民生活用电量的比重占主导地位，则相反，年负荷特性曲线波动较剧烈，季不均衡系数较小，相应的最大负荷利用小时数也较小。

(3)社会影响因素

社会影响因素包括:人均国内生产总值(元)、城镇居民人均可支配收入(元)等。

随着城市的发展，人均国内生产总值和城镇居民人均可支配收入的增加，居民生活用电增加，年负荷特性曲线波动加剧，季不均衡系数减小。

1.2 加权关联度确定

灰色关联度分析［10］是基于行为因子序列曲线几何形状的相似程度来判断其联系是否紧密，曲线越接近，相应序列之间的关联度就越大。它是确定因子间影响程度或因子对主行为的贡献程度而进行的一种分析方法。灰色关联分析的目的是寻找各因素间的主要关系，能够确定哪些是不可忽视的相关行为因素，从中找出各相关影响因素对主行为的关联程度，从而掌握事物发展的主要矛盾。因此，它特别适合数据有限、没有原型、复杂而且具有不确定性问题的分析和评价。

灰色关联度分析弥补了采用数理统计方法作系统分析所导致的缺陷。它对系统样本量的多少和样本有无规律都同样适用，而且计算量小，十分方便，更不会出现量化结果与定性分析不符的情况。为此，在季不均衡系数影响因素中引入灰色关联度分析理论来对其进行综合定量分析。

1.2.1 序列矩阵

季不均衡系数的影响因素序列(子序列)不止一个，可将季不均衡系数用ρ表示，相关因素子序列用X0、X1、…，Xi来表示，所构成的序列矩阵为

式中，ρ列表示季不均衡系数各年的数值;Xi列表示影响因素序列各年的数值。

1.2.2 初值像矩阵

不同序列，数值可能相差甚远，甚至量纲不具有可比性，因此首先要经过规范化处理。采用首归一化处理，以便于比较，计算公式如下。

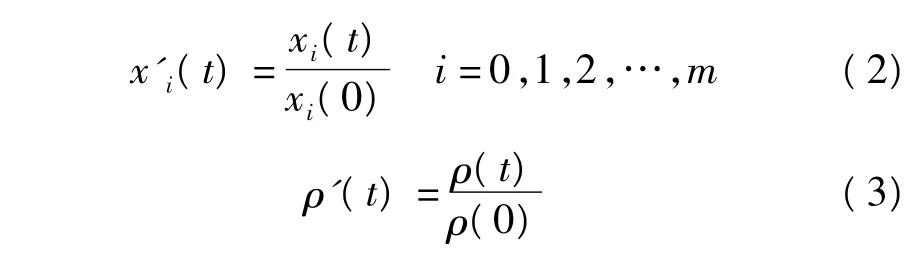
初值(无量纲化)矩阵为

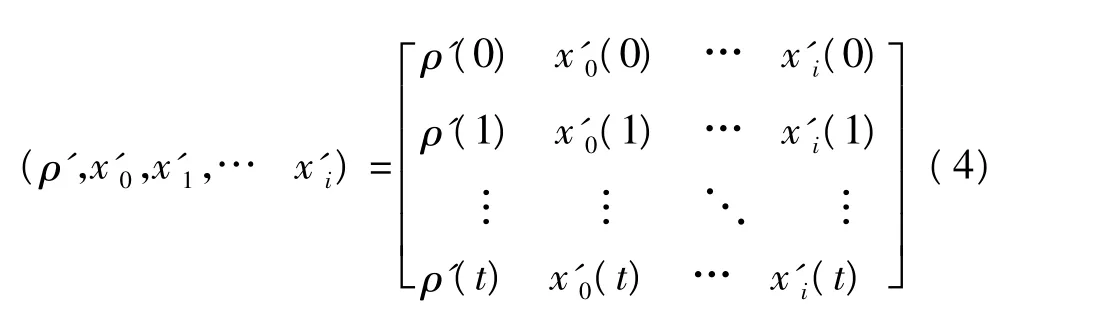
1.2.3 差序列矩阵

若将系统因素集合中的各个因素视为空间的点，将每个因素对于不同时刻、不同指标、不同对象的观测数据视为点的坐标，就可以在特定的n维空间中研究各因素之间或因素与系统特征之间的关系，得出差序列的计算公式如下。

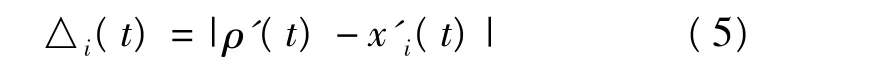
差值矩阵为

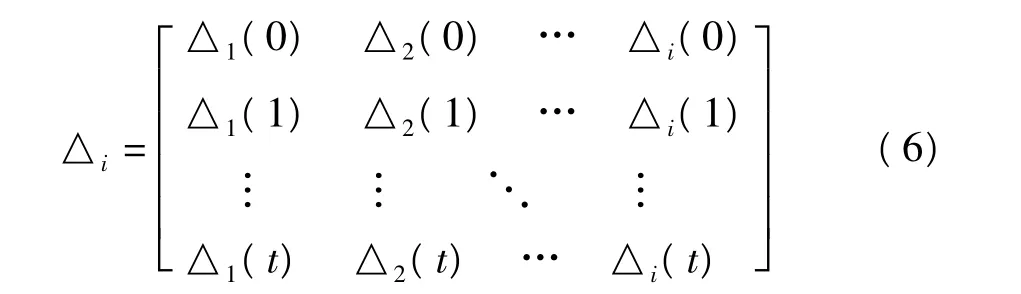
求两级最大差与最小差为

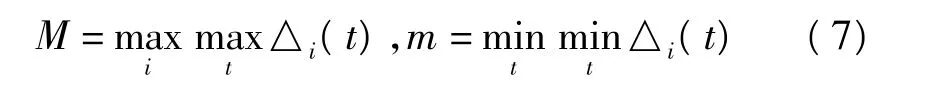
1.2.4 关联系数矩阵

关联系数主要是计算季不均衡系数与影响因素子序列之间在不同时间段的关联性，计算公式如下。

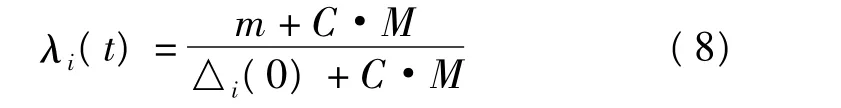
式中，C∈(0，1)为分辨系数，通常取0.5。通过公式(8)计算出各年份的季不均衡系数与影响因素子序列的关联系数，形成关联系数矩阵为

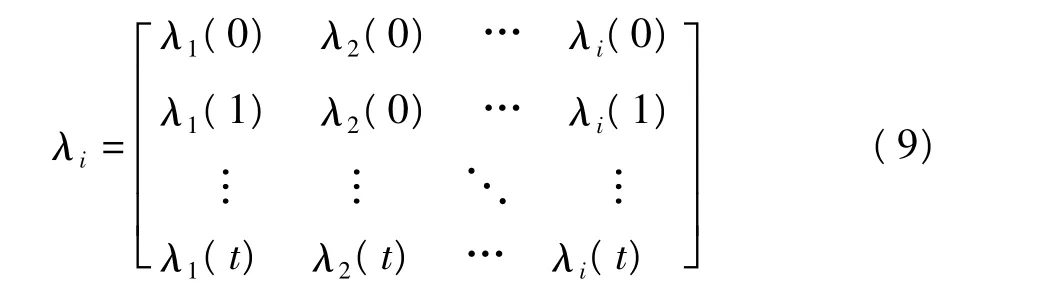
1.2.5 确定各个年份权重的具体步骤

设系统有待进行重要性比较的指标集F={f1，f2，…，fn}，fi为第 i个指标，i=1，2，…，n。n 为指标总数。

为了解决AHP中判断矩阵的一致性问题，将AHP中构造判断矩阵变成构造模糊一致判断矩阵，即采用模糊层次分析法(FAHP)［12-15］，其可作如下表述。

(1)建立优先关联矩阵

其中s(i)和s(j)分别表示指标fi和fj的相对重要性程度。

(2)将优先关系矩阵F改造成模糊一致矩阵A，即先对F按行求和，记为

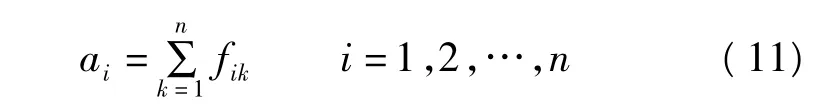
然后作变换得

由此建立的判断矩阵可以保证模糊一致性。

(3)权重值ωi的计算公式

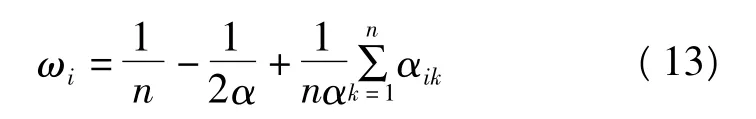
式中，i=1，2，…，n;α 满足 α≥(n-1)/2 的参数。当阶数n比较大时，将参数α取值为α=(n-1)/2，有助于提高对元素f1，f2，…，fn的相对重要程度的分辨率。

1.2.6 加权关联度

为了计算主特征序列与影响因素子序列间的关联度，必须将各个时间段的关联系数进行加权求和，得出它们之间的关联度，计算公式如下。

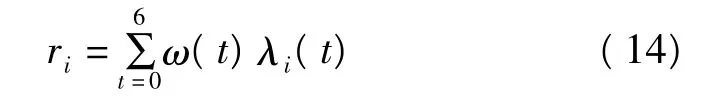
式中，ω(t)为各个年份的权重。

2 算法分析

通过以上的分析，可以建立相应的算法，该算法在历史数据的基础上，经过数据处理得到各影响因素对季不均衡系数的加权关联度，找出季不均衡系数的主要影响因素。计算结果用于分析历史年负荷特性和指导未来年负荷特性的预测。

(1)输入数据

该算法的输入数据为季不均衡系数和各影响因素的分年度数据。这些数据来源于一个地区的统计年鉴、政府工作报告和电网规划报告。

(2)假设条件

计算各年份权重的计算中，以“远小近大”的原则，假设近期年份的重要性程度大于远期年份的;公式(13)中参数α取值为α=(n-1)/2。

(3)输出数据

该算法的输出数据为各影响因素对季不均衡系数的加权关联度，定量地区分了各影响因素对季不均衡系数的影响程度。

综上所述，具体流程框图如图1所示。

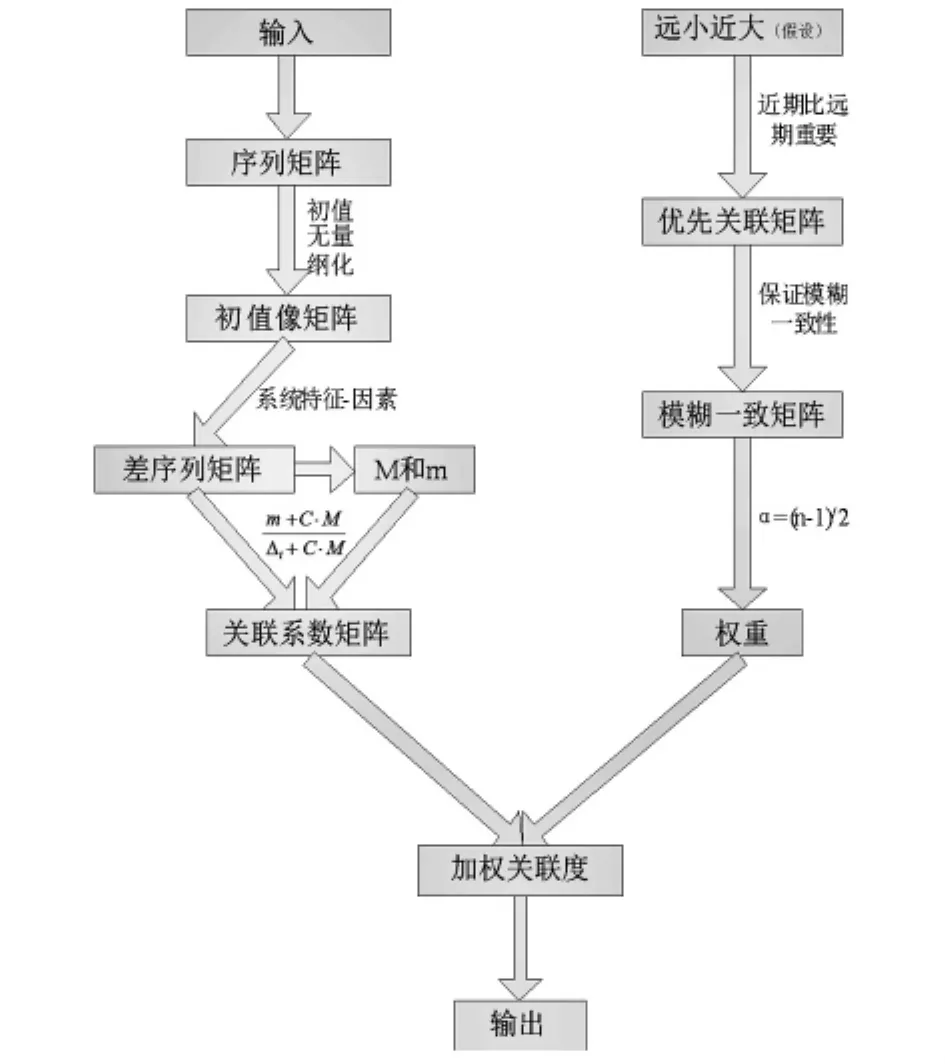
图1 流程框图

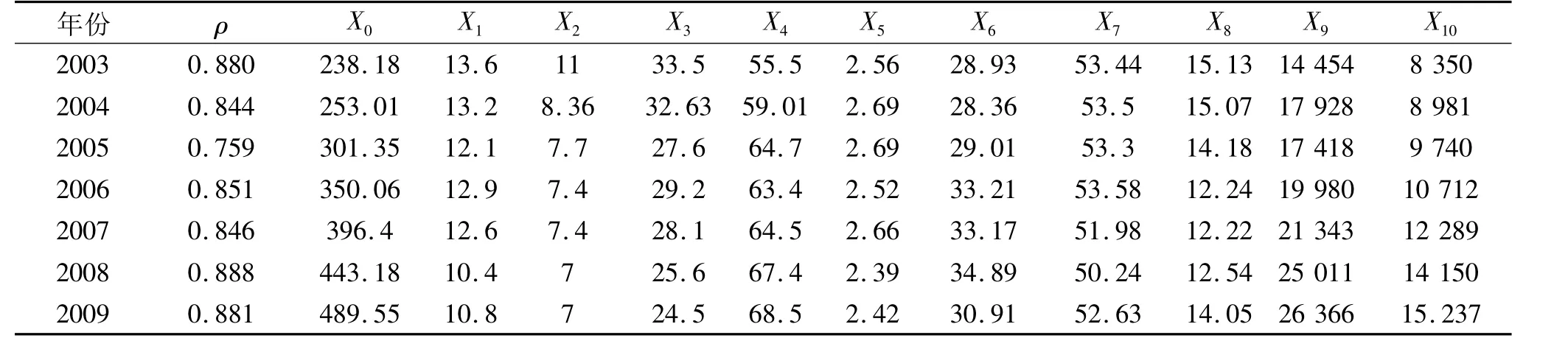
表1 基础数据列表

3 实际应用

针对一实际系统，根据收集到的相关数据，利用以上算法，得到了各影响因素对季不均衡系数的加权关联度。

为验证算法的正确性，选取表1中的两组数据来进行对比分析。

①取2002～2009年数据，分析季不均衡系数的主要影响因素;

②取2003～2010年数据，分析季不均衡系数的主要影响因素。

根据算法的具体流程计算如下。

(1)输入数据

表1中的统计数据来自一旅游城市政府工作报告和电网规划报告。

(2)利用“远小近大”的原则和公式(10)～(13)来确定各时间段的权重，权重为

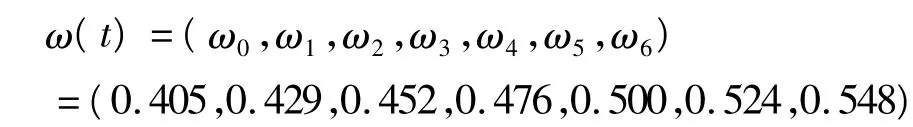
(3)输出数据

根据公式(14)，加权关联度矩阵为

(4)结果分析

根据两组数据计算结果，第三产业用电量比重对季不均衡系数影响均最大，各影响因素与季不均衡系数的加权关联度如图2所示。

计算表明:第三产业用电量比重对季不均衡系数影响最大，这与该旅游城市的性质相一致。根据实际调研，该城市第三产业用电量比重连年在50%左右，且在今后发展中保持在较高水平，使得年负荷特性曲线波动加剧，对季不均衡系数影响最大。

第三产为的不断增长，导致第三产业用电量比重进一步加大，在各影响因素中仍战友主导地位。在未来几年，该地区年负荷特性曲线波动将不断加剧，季不均衡系数逐步减小。

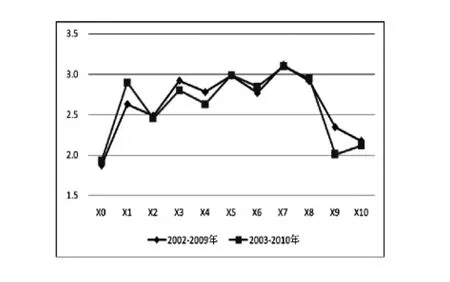
图2 结果分析图

该算法得出了委不均衡系数的主要影响因素，与该城市的实际情况相吻合，为负荷特性的历史分析和未来预测提供了依据。

4 结论

(1)对季不均衡系数影响因素的关系进行了研究，运用灰色关联度分析理论来区分各影响因素的权重，找出一个地区季不均衡系数的主导影响因素，并且该分析过程较易推广到其他地区。

(2)对季不均衡系数的研究可以运用在地区电网规划中，对现状年负荷特性进行分析，并对年负荷特性的预测提供指导意义。不同负荷的特性制定相应的分时电价措施，可最大限度地达到削峰填谷的作用，提高电网经济运行效益。

(3)灰色关联度分析法还可以用于其他参数的分析，如平均日负荷率γ、平均月负荷率σ等。通过参数的分析，可以掌握一个地区日负荷曲线和年负荷曲线的主要影响因素，从而指导负荷特性的预测。

［1］赵希正，周小谦，姜绍俊.中国电力负荷特性分析与预测［M］.北京:中国电力出版社，2002.

［2］陈健，刘明波，樊亚亮，等.广州电网负荷特性分析［J］.电力系统及其自动化学报，2009，21(6):78-83.

［3］叶刚健，蒋金良.汕头电网负荷特性分析与预测［J］.电力系统及其自动化学报，2004，16(6):55-59.

［4］赵永良，易武，谢开贵.固原电网负荷特性分析［J］.电网技术，2007，31(2):230-232.

［5］姜勇.南京市居民夏季用电负荷特性分析［J］.继电器(Relay)，2003，31(4):24-26.

［6］徐方龙，谢国栋，黄苏融，等.上海市区供电局电力负荷特性分析［J］.上海大学学报(自然科学版)，2000，6(3):222-226.

［7］杨宗麟.华东电网负荷特性分析预测［J］.华东电力2008，36(5):50-52.

［8］张吉军.模糊一致判断矩阵3种排序方法的比较研究［J］. 系统工程与电子技术，2003，25(11):1370-1372.

［9］葛少云，闫大威，董智.基于模糊综合评判的城市电网电缆化改造［J］.现代电力，2005，22(3):37-40.

［10］霍成军.电力系统负荷特性分析研究［D］.天津:天津大学电气与自动化工程学院，2007.

［11］仲伟宽.数据挖掘技术在负荷特性分析中的应用［D］.南京:东南大学电气工程学院，2006.

［12］杜海文，孟领坡，马洪斌.防空导弹制导雷达综合抗干扰能力评估［J］.火力与指挥控制(Fire Control＆Command Control)，2004，29(5):54-56，61.

［13］张江，应俊，王琼，等.基于FAHP的电力变压器系统的脆性分析［J］.控制理论与应用，2004，23(7):9-12.

［14］沈又幸，范艳霞，谢传胜.基于FAHP法的风电项目后评估研究［J］.电力需求侧管理，2008，10(6):16-18.

［15］高会生，冉静学，孙逸群.基于改进的FAHP电力通信网风险评估［J〛.系统工程理论与实践，2008，(3):133-138.