硬壳层软土地基竖向附加应力分布研究

张军辉，江伟唯，郑健龙

硬壳层软土地基竖向附加应力分布研究

张军辉，江伟唯，郑健龙

（长沙理工大学公路工程教育部重点实验室，长沙 410004）

采用有限元法对条形均布荷载作用下硬壳层软土地基竖向附加应力进行数值模拟，得到了不同厚宽比及模量比时层间竖向附加应力系数，编制了表格以便查询；通过二元回归分析得到了厚宽比、模量比与层间竖向附加应力系数的近似函数关系；结合“等效深度”概念，推导了一个硬壳层软土地基竖向附加应力分布的计算公式，并通过实例验证了计算公式的有效性。

硬壳层；软土地基；竖向附加应力；沉降；二元回归分析

1 概 述

由于硬壳层的存在，上覆硬壳层的软土地基附加应力分布与均质地基不同。室内模型试验［1，2］和工程实践［3－5］均表明硬壳层将导致其下软土层中应力扩散。因此，建立在均质、各向同性的弹性半无限空间体基础上的Boussinesq解将不再适用于硬壳层软土地基附加应力计算。目前，对于硬壳层软土地基附加应力计算方面的研究尚不多见，主要集中在层间竖向附加应力系数的计算方面［6，7］，不便于工程应用。基于此，本文采用有限元法和二元回归分析，在得到硬壳层软土地基层间竖向附加应力分布系数后，结合“有效深度”概念，建立了硬壳层软土地基竖向附加应力分布的简明计算方法，并与其他方法进行对比，验证了本文计算方法的正确性。

2 数值模型的建立与验证

为进行硬壳层软土地基附加应力分布分析，假定土体为各向同性、均质的理性线弹性体，且层间完全连续，并采用有限元程序Ansys10．0建立数值模型。根据试算，水平宽度与深度分别取160 m和80 m。考虑到模型的对称性，取一半进行建模，如图1所示。模型的左右边界水平向位移为零，底部为竖向和水平向约束。加载为条形均布荷载，单元采用高阶二维八节点单元。

为验证模型合理性，取上下土层性质相同，模拟均质地基情况，数值模拟结果与Boussinesq解如图2所示。从图中可知，条形荷载作用下，荷载中心下任意一点的附加应力系数（任意一点的竖向应力与表面荷载的比值）的解析解与数值解非常接近，说明计算模型合理，可用于进一步的计算。

图1 有限元模型Fig．1 Finite elem entm odel

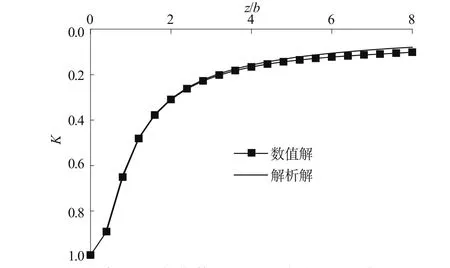
图2 条形均布荷载下数值解与解析解的对比Fig．2 Numerical and analytical solution under uniform strip load

3 层间竖向附加应力系数计算

已有研究表明［6］，影响硬壳层软土地基层间竖向附加应力系数的因素是硬壳层与软土层的压缩模量之比（简称模量比E1／E2）以及硬壳层厚度H与荷载分布宽度B之比（简称厚宽比H／B）两个因素，而与硬壳层与软土层的泊松比关系不大。根据实际工况，本文取硬壳层的泊松比为0．3，软土层的泊松比为0．45，计算了不同模量比及厚宽比时的层间附加应力系数Kc，如表1所示。

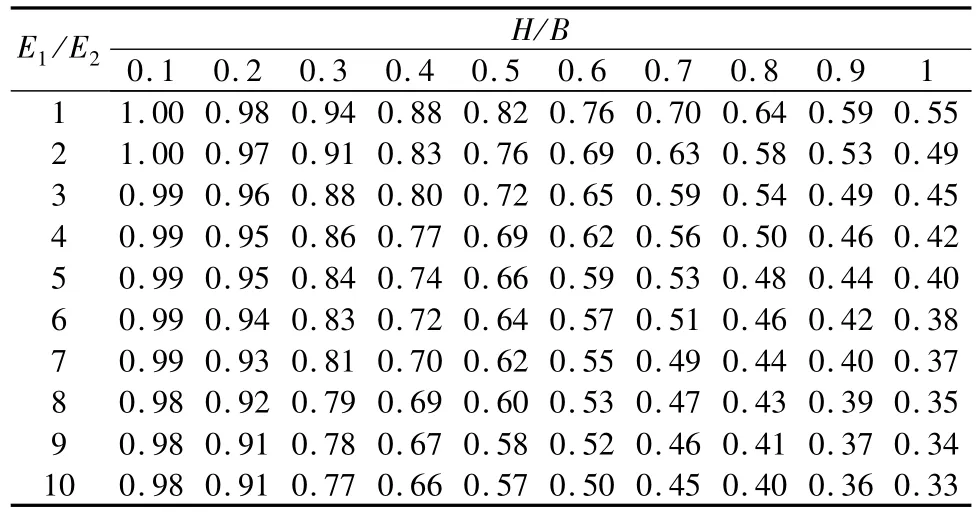
表1 条形均布荷载分布下层间竖向应力分布系数KcTable 1 Coefficients of vertical additional stress Kcunder uniform strip load

由于H／B在0．1时层间附加应力系数变化很小，且E1／E2＝1为均质地基，因此在2≤E1／E2≤10，0．2≤H／B≤1范围内，本文通过二元回归分析得到了硬壳层软土地基层间附加应力系数Kc与H／B和E1／E2的回归关系，相关系数R2＝0．99，回归的函数为

回归函数计算值与数值解的相对误差见表2，除了当H／B＝0．2、E1／E2＝2和3时相对误差大于5%以外，其它回归函数计算值与数值解相对误差均小于5%。因此式（1）可用于条形均布荷载作用下硬壳层软土地基层间竖向附加应力系数的计算。

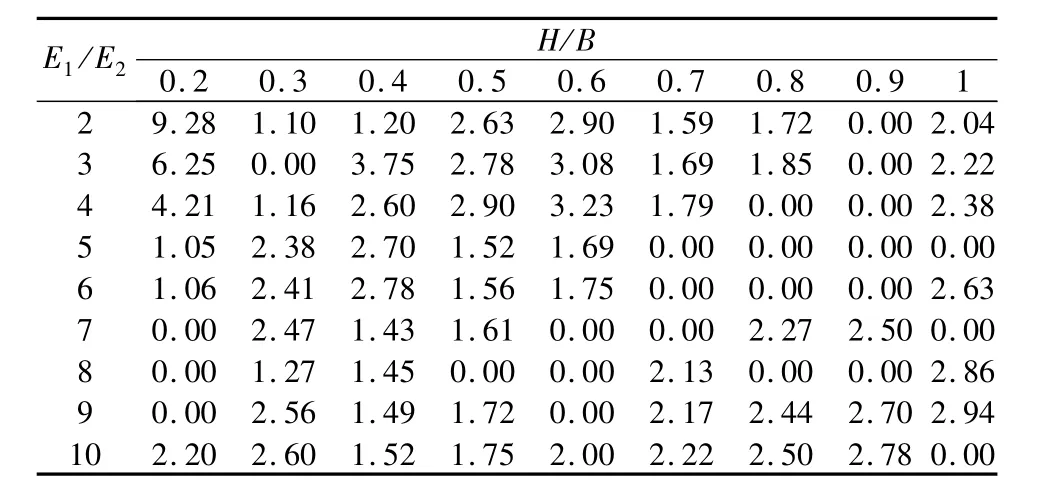
表2 回归函数计算值与数值解的相对误差Table 2 Relative errors of regressive and num erical solution%

4 竖向附加应力分布计算

前文仅计算了层间附加应力的大小，但整个地基深度附加应力分布的计算目前还没有相应的公式，已有研究通常采取“等效深度”的概念来计算附加应力分布，步骤如下：

（1）通过查表（应力扩散角法或应力系数法）获得层间应力系数；

（2）在得到层间应力系数后，根据均质线弹性理论解计算出下卧层顶面的等效深度Ze，等效原理是硬壳层软土地基分界面上的应力系数与均质线弹性地基Ze深度处的应力系数相等，等效图见图3；

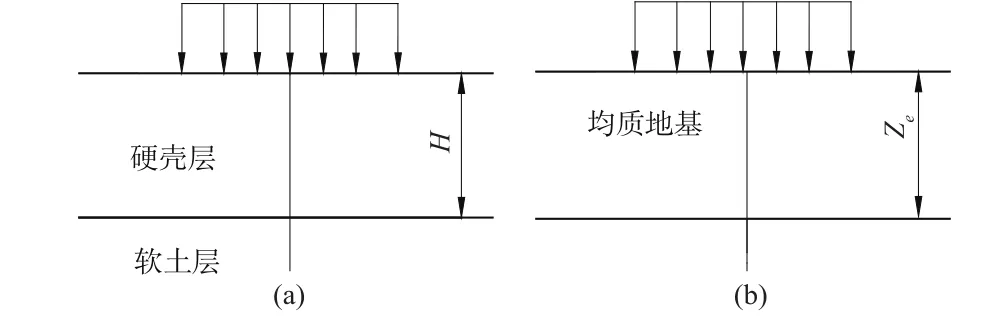
图3 等效深度示意图Fig．3 Sketch of equivalent depth

（3）求得Ze后，按照均质地基线弹性理论解计算下卧层中各点的附加应力；

（4）硬壳层中的应力分布则近似按照线性分布来计算。这样就可以得任意深度的附加应力大小。

结合以上思路，本文推导了硬壳层软土地基附加应力分布计算公式，步骤如下。

4．1 硬壳层软土地基层间竖向附加应力系数Kc的计算

当已知参数E1，E2，H，B，即可采用式（1）来计算硬壳层软土地基层间附加应力系数Kc。

4．2 等效深度Ze的计算

对于条形均布荷载作用下半无限均质地基的中心竖向应力分布系数解答如式（2）［1］：

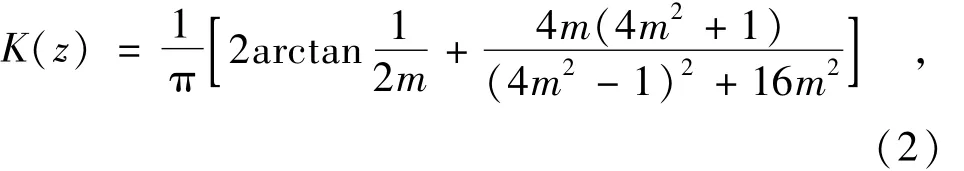
其中，m为计算深度z与荷载分布宽度B的比值。若已知K（z），通过式（2）求解右侧的m比较复杂。通过回归发现m≥0．1时，可以用式（3）替代式（2）。这样，若已知K（z），欲求m，可以非常方便地通过式（3）实现。用式（3）可替代式（2）的相对误差见表3。

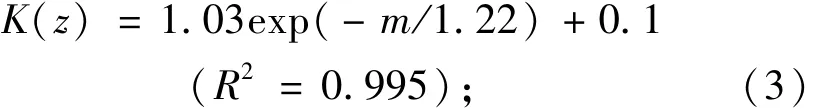
根据前文所述，只要将硬壳层软土地基层间附加应力系数Kc与均质地基竖向应力分布系数K（z）取等值，即将通过式（1）计算得到的Kc代入式（4）中，即可得到等效深度Ze：

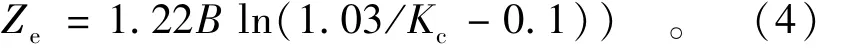
4．3 硬壳层软土地基附加应力分布的计算

将硬壳层中的应力分布近似按线性分布来计算，其下软土层中的应力按照均质地基线弹性理论解计算，即可得到硬壳层软土地基附加应力计算公式。设表面荷载大小为P0，则层间竖向附加应力为P0·Kc，可得硬壳层软土地基附加应力计算公式：

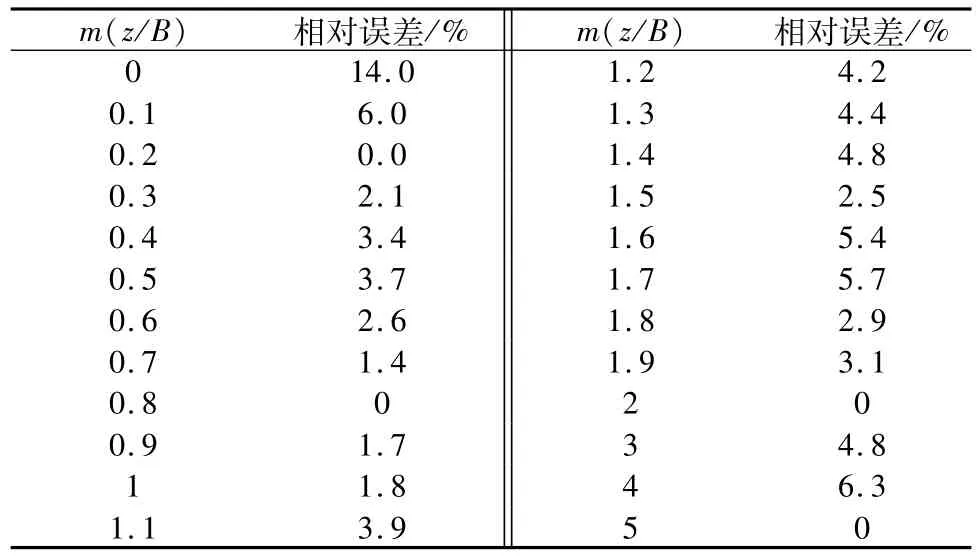
表3 式（3）代替式（2）的相对误差Table 3 Relative errors of substituting equation（3）for equation（2）

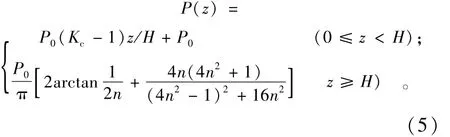
其中，n＝（z＋Ze－H）／B，参数Kc以及Ze分别按式（1）和式（4）来计算，式（5）的适用条件为2≤E1／E2≤10和0．2≤H／B≤1。

5 算例分析

硬壳层软土地基上承受条形局部荷载作用，该硬壳层厚H＝5 m，荷载分布B＝10 m，硬壳层与软土层压缩模量分别为31．8 MPa和3 MPa，有效重度分别为18．4 kN／m3和17．5 kN／m3。表面荷载作用大小为100 kPa，硬壳层的与软土层的e-p曲线见表4，软土层计算深度为20 m。分别采用Boussinesq解法［1］、有限元法、当层法［7］以及本文推导的简明计算公式进行附加应力分布求解，然后通过分层总和法［1］进行主固结最终沉降计算。

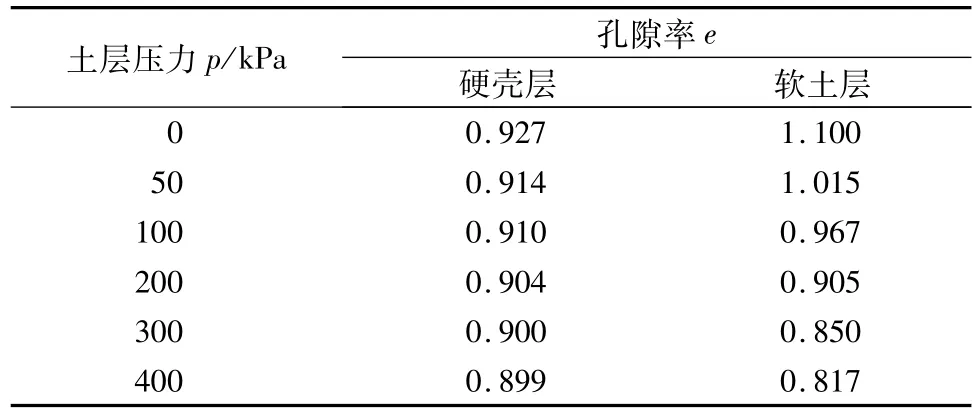
表4 硬壳层与软土层e-p关系Table 4 e-p relationship between upper crust and soft soil

图4和表5分别为各种方法得到的附加应力分布和采用分层总和法计算的最终主固结沉降。可以看出，采用分层总和法计算最终主固结沉降时，本文推导的公式与有限元法最为接近，相对误差仅为5．6%，Boussinesq解高估了沉降值，而当成法则大大低估了沉降值，因此都不能正确地反映硬壳层软土地基应力扩散效应。由于本文附加应力计算公式是根据双层地基理论得到的，较好地反映了硬壳层的扩散效应，得出的沉降结果更符合实际，且公式简单，便于推广应用。

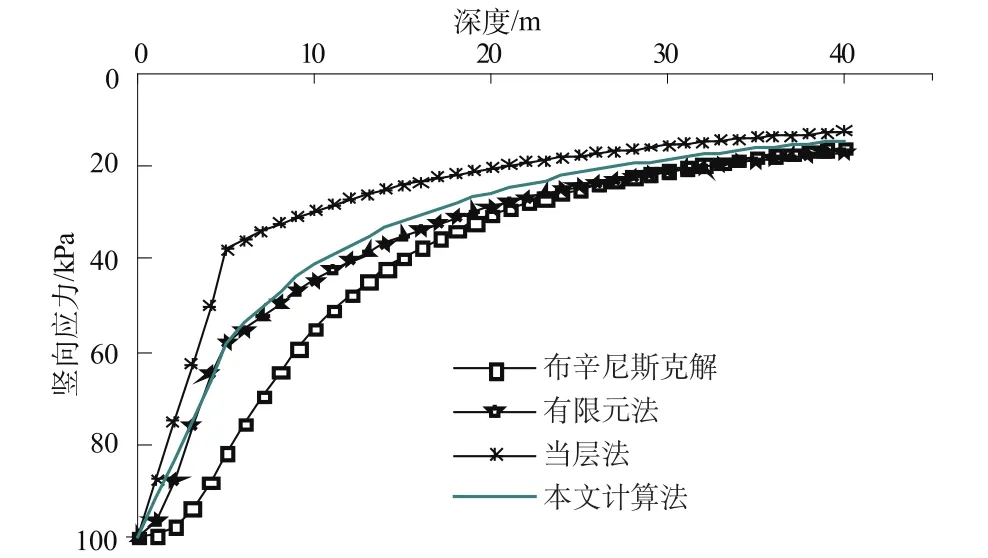
图4 各种方法求解附加应力分布Fig．4 Additional stress distribution by differentmethods

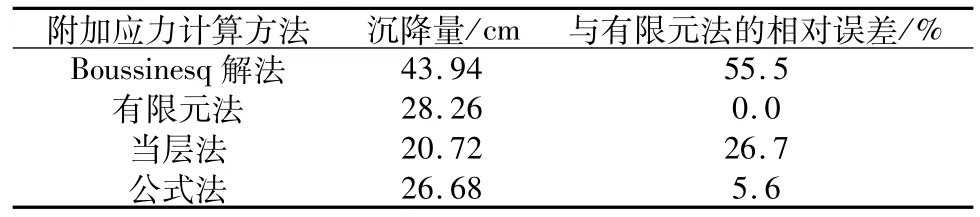
表5 不同附加应力分布下的沉降值Table 5 Settlement calculated by different calculation methods

6 结 语

本文采用有限元法建立了平面应变条件下的双层地基计算模型，通过二元回归分析得到了硬壳层软土地基层间竖向附加应力系数，并结合“有效深度”概念推导了硬壳层软土地基竖向附加应力分布的计算公式。由于计算公式是根据双层地基理论求得，能反映硬壳层的应力扩散效应，通过分层总和法得出的计算结果更加符合实际，同时公式形式简单，计算参数容易获取，便于推广应用。

［1］ 高大钊，袁聚云，谢永利，等．土质学与土力学［M］．北京：人民交通出版社，2001．（GAO Da-zhao，YUAN Ju-yun，XIE Yong-li，et al．Geology and Soil Mechanics［M］．Beijing：China Communications Press，2001．（in Chinese））

［2］ 唐建中．双层地基应力扩散的特性研究［J］．地基处理，1993，4（2）：25－31．（TANG Jian-zhong．Research on Properties of Stress Dispersion of Double-Layer Foundation［J］．Foundation Treatment，1993，4（2）：25－31．（in Chi-nese））

［3］ 杨果林．含软弱下卧层的双层地基工程特性试验研究［J］．工程勘察，1998，3（l）：l－5．（YANG Guo-lin．Test Research on Engineering Properties of Double Layer Ground Containing Weak Underlying Stratum［J］．Engi-neering Investigation，1998，3（l）：l－5．（in Chinese））

［4］ 张留俊．高路堤下软土硬壳层工程性质的研究［J］．公路，1999，（7）：5－9．（ZHANG Liu-jun．Research on Engi-neering Properties of Upper Crust of Soil Foundation of High Embankment［J］．Highway，1999，（7）：5－9．（in Chinese））

［5］ 吴邦颖，曹正康．公路软土路基人造硬壳层处理及研究［J］．路基工程，1996，（4）：39－46．（WU Bang-ying，CAO Zheng-kang．Treatment and Research on Artificial Crust of Soft Soil Foundation of Highway［J］．Subgrade Engineer-ing，1996，（4）：39－46．（in Chinese））

［6］ 彭月明，张铁壮，窦远明．硬壳层对软土地基沉降特性影响的研究［J］．河北工业大学学报，2007，36（1）：101－105．（PENG Yue-ming，ZHANG Tie-zhuang，DOU Yuan- ming．Study on Settlement Characteristic Impacts of Hard Shell Course to Soft Ground［J］．Journal of HebeiUniver-sity of Technology，2007，36（1）：101－105．（in Chinese））

［7］ 宋文刚，房兆祥，王晓化．含软弱下卧层双层地基内应力简便计算初步探讨［J］．工程勘察，1993，8（6）：7－12．（SONGWen-gang，FANG Zhao-xiang，WANG Xiao-hua．Stress Calculation of Double Layer Ground Containing Weak Underlying Stratum［J］．Engineering Investigation，1993，8（6）：7－12．（in Chinese））

［8］ 徐 洋，谢康和．复合地基的平面应力扩散效应［J］．土木工程学报，2002，35（2）：57－60．（XU Yang，XIE Kang-he．A Study on Effect of Plane Stress Dispersion in Composite Ground［J］．China Civil Engineering Journal，2002，35（2）：57－60．（in Chinese） ）

（编辑：姜小兰）

Vertical Additional Stress of Soft Soil Foundation w ith Upper Crust

ZHANG Jun-hui，JIANGWei-wei，ZHENG Jian-long
（Key Laboratory of Highway Engineering of Ministry of Education，Changsha University of Science＆Technology，Changsha 410004，China）

The distribution of vertical additional stress of soft soil foundation with upper hard crust under uniform strip load is numerically simulated by finite elementmethod．Through the simulation，the coefficients of interlayer vertical additional stresswith different ratios of crust thickness to load width and ratios of crustmodulus to soft soil modulus are obtained，and tableswith these coefficients are given for reference．Furthermore，an approximate func-tion of these coefficients versus ratio of crust thickness to load width and ratio of crustmodulus to soft soil is presen-ted using binary regression analysis．Finally，a calculation formula for vertical stress of soft soil foundation with up-per hard crust is deduced based on the concept of equivalent depth，and the validity of this formula is verified by case calculation．

crust；soft soil foundation；vertical additional stress；settlement；binary regression analysis

TU431

A

1001－5485（2011）05－0042－04

2010-06-22；

2010-08-23

交通部西部交通科技项目（2009－318－000－062）；交通部西部交通科技项目应用基础研究项目（2009－319－825－090）；湖南省教育厅项目（08C100）；长沙理工大学公路工程省部共建教育部重点实验室开放基金资助项目（kfj090105）

张军辉（1978-），男，河南驻马店人，副教授，从事软基处理、特殊土路基处治等方面研究，（电话）0731-85258255（电子信箱）zjh-seu＠163．com。