扰流子强化换热的数值模拟分析研究
马小晶,程伟良,崔春华
(新疆大学电气工程学院,新疆 乌鲁木齐 830046)
0 引言
换热设备是工业部门中使用最广泛的工艺设备之一。为了节能降耗,提高经济性,对换热设备进行强化换热的研究一直是传热学研究的热点[1,3]。目前在许多发电机组的换热设备中都安装了用于强化换热的各种结构的扰流子。如,安装在凝汽器铜管内的螺旋纽带装置,它利用循环水的自身流动驱动纽带自动旋转和径向摆动,使水旋涡运动不断冲刷管壁产生强烈扰动和径向混合,基本消除了层流边界层,实现了强化传热的同时还能自动除垢防垢,达到机组节能降耗的目的。文献[4]中提出了以速度场和热流场之间的场协同情况来判断换热的强化状况,通过对边界层的流动进行能量方程分析,发现在其他条件相同的情况下,温度与速度梯度之间的协调越好,换热就越强烈[4,7]。本文在场协同原理基础上,采用数值模拟方法,分析插入管内的不同结构扰流子时的速度场和温度场,旨在研究不同形状扰流子的换热特性及强化机理。
1 物理问题与数学描述
二维的层流边界层,其场协同的数学描述的能量方程[8]
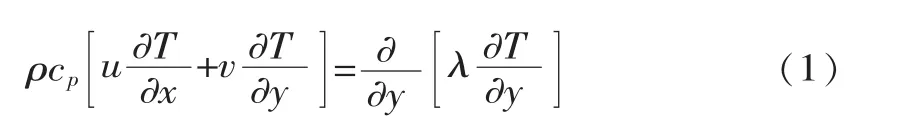
对式(1)积分并无量纲化得

从式(2)可以看出,对流换热的强度不仅与流体和固体壁面的温差、流动速度和流体物性等有关,还和流体速度矢量与热流矢量的夹角有关。场协同原理就是指速度场与温度梯度两个矢量场的协同,即一定的速度和温度梯度下,减小二者之间的夹角可强化对流换热,所以应尽可能使两者平行。
文献[6-7]中通过插入有扰流子的平行板通道和圆管验证并解释了场协同原理。基于该理论,可设计不同形式的管内插入物,通过phonices软件对管内流场和温度场进行数值模拟,分析比较不同结构及尺寸的扰流子对换热的影响。
为便于分析,在对管内传热性能进行数值模拟时,可进行一些假设:管内流动近似看为轴对称的稳态流动;流动介质为空气,假定其为不可压缩流体;流体的各物性为常数,不随温度而改变;忽略重力的影响;只考虑扰流子结构对管内温度场的影响,忽略管内扰流子自身的传热与导热。设定其边界条件是:进口条件为入口流速0.1~1 m/s,并假定进口截面上各点流速均相等,流体的进口温度为300 K;壁面为无滑移情况,壁上流体速度为零,壁厚为1 mm,壁面温度设为恒定400 K;计算时设定在流体中,扰流子只起到改变流场的作用而不参与换热;出口为外界大气压环境。
计算时气体流动湍流模型选取为标准k-ε模型,采用SIMPLEC算法进行压力和速度耦合求解。
在圆管内沿轴线方向采用了如图1所示的4种不同结构的扰流子,在其他参数相同的条件下进行数值模拟,从而便于进行对比分析扰流子的结构对换热的影响。
另外,还针对圆棒式扰流子,取圆棒直径d分别为6,8、10 mm,在其他参数相同的条件下进行数值模拟,分析扰流子的尺寸对换热的影响。

图1 不同结构的扰流子 (尺寸单位:mm)
基于圆管和扰流子结构具有轴对称性,为减少计算量,将该计算模型简化为二维平面问题进行处理,计算所用的网格划分采用均分网格,将模型划分为52×240×1个网格,采用笛卡尔直角坐标,故数值计算的控制方程采用直角坐标系下二维不可压缩稳态流动的连续方程,其对应的Navier-Stokes动量方程和能量方程 (忽略流体质量力)

所需的平均表面传热系数为

计算时的压降为

其中,Δtm对数平均温差;A为换热面积;φ为热流量;ρ和cp取为进、出口的算术平均值。
2 计算结果和分析
2.1 不同直径的圆棒形扰流子对换热及压降的影响
在流动空气从管内的被加热时,由于空气的对流换热系数比较小,也就是说,气侧的热阻大,为提高换热,考虑在管内沿轴向插入扰流子。这里首先考虑插入圆棒式扰流子进行模拟计算分析。图2为圆棒式扰流子直径d分别为6、8、10 mm的情况下,管内平均换热系数h和压降Δp随入口雷诺数的变化关系,图2中实线表示平均换热系数h随入口雷诺数的变化曲线,点虚线表示压降Δp随入口雷诺数的变化关系。
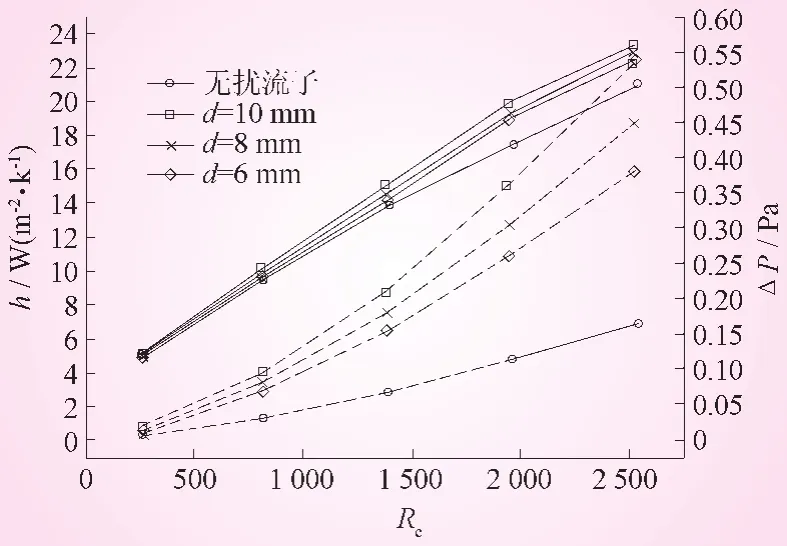
图2 圆棒直径对平均换热系数h和压降Δp的影响
从图2中可看出,在入口雷诺数Re从0到2 500的变化范围内,平均换热系数和流动阻力都随着圆棒式扰流子直径和入口雷诺数的增大而增大。所不同的是随着入口雷诺数的增大,不同直径的圆棒扰流子所对应的平均换热系数的差值不大,但不同直径扰流子所对应的流动阻力的差值较大。由此可知,增大扰流子直径在一定程度上可增强对流换热效果,但流动阻力也随之增大;并且入口雷诺数越大,流动阻力的增幅远大于平均换热系数的增幅。也就是说,在设计加工圆棒扰流子时,其直径不宜太大。即,要保持一定合理的流动通道,才能达到即有一定的增强换热效果,同时又不致风机的耗功太大。这样既保证了效率的提高,又利于节能;而不要一味地提高换热效率,致使其运行成本过高,不能得到实际应用。
2.2 不同形式扰流子的影响
进行模拟计算的插入扰流子的形式分为4种,即:圆棒式扰流子、椭球式、球形链式及椭球形链式。图3为不同结构扰流子对管内平均换热系数h和压降Δp的变化关系。其中圆棒式扰流子直径取d=10 mm。
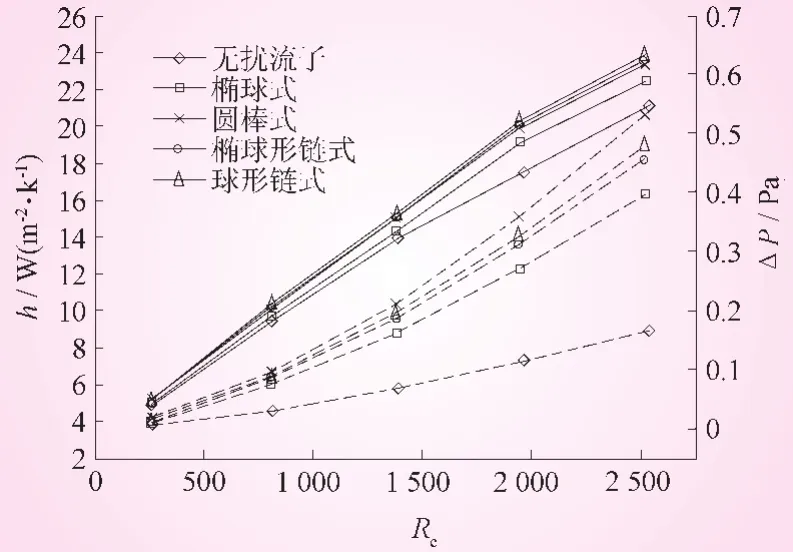
图3 不同形式扰流子对换热和压降的影响
由图3可看出,平均换热系数h和压降Δp随入口雷诺数的变化趋势,其中实线表示平均换热系数h随入口雷诺数的变化曲线,虚线表示压降Δp随入口雷诺数的变化关系。在所研究的雷诺数范围内,有扰流子与无扰流子的平均换热系数h和压降Δp都随入口雷诺数Re的增大而增大,只要插入扰流子,不论是何种扰流子,其压降和平均换热系数都大于无扰流子的情况。二者不同的是,不同结构扰流子的流动阻力相差较大,圆棒式扰流子的流动阻力最大,球形链式的略大于椭球形链式。从图3还可以看出,虽然扰流子的结构对换热具有一定影响,但平均换热系数相差并不大,其中球形链式扰流子的平均换热系数最大,略大于椭球形链式和圆棒式扰流子,椭球式扰流子的平均换热系数最小。
为了便于对图3中的一些结论进行进一步分析,又对流经管内的入口速度为u=0.1 m/s时,无扰流子、椭球式、圆棒式、椭球形链式及球形链式扰流子的分别进行了数值模拟计算,并获得了其对应的温度及速度分布 (见图4~图8)。

图4 无扰流子时的光管内温度分布 (温度单位:℃)
由图4可知,无扰流子光管的温度梯度方向沿径向分布,而光管的流线方向几乎与管道轴向平行,流速方向即为流线方向,而温度主要是沿圆管径向发生变化的,变化最大的方向即温度梯度。可看出,速度矢量与温度梯度方向所成的角接近90°,由场协同原理可知,二者的协调效果很差,对流换热效果不是很好。

图5 插入椭球式扰流子时的管内温度及速度分布

图6 插入圆棒式扰流子时的管内温度及速度分布
由图5和图6可知,对于插入椭球式和圆棒式扰流子的圆管流道内部,在扰流子两端附近流速增大,且该处流速分布明显地发生了变化。由此可看出,温度梯度方向与流速方向的夹角变小,即此时温度梯度场与速度场的协同效应得到加强,对流换热效果较好;同时,圆棒式扰流子末端处有漩涡存在,增强换热,所以与椭球式扰流子相比,插入圆棒式的换热效果较椭球式绕流子好。

图7 椭球形链式扰流子存在时的温度及速度分布
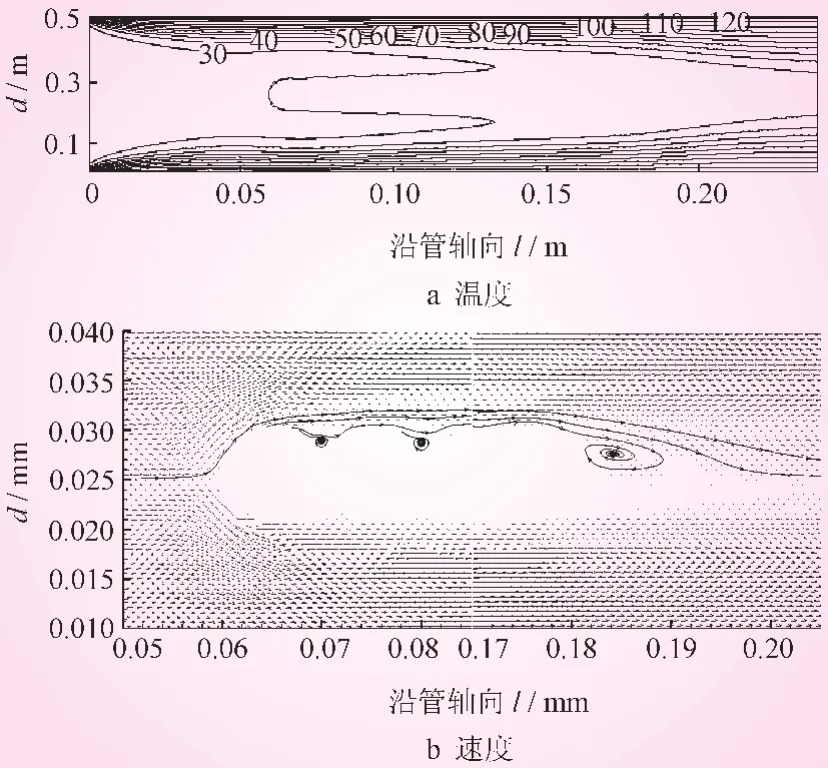
图8 在球形链式扰流子插入管内时的温度及速度分布
由图7和图8可知,在圆管内部插入椭球式和球形链式扰流子增强换热时,由于链式结构的明显特征,在每颗球体连接处的近壁面附近流线方向发生了明显变化,并伴有漩涡产生,增强了对流换热;同时,当扰流子长度相同时,球形链式比椭球形链式具有更多的球体颗粒,因此伴随的漩涡数量较多,所以换热效果更好。
3 结论
目前在许多汽轮发电机组的换热设备中都有用于强化换热的各种结构的扰流子存在,其应用不仅可自动除垢防垢,还可达到节能、降耗及增效的目的。当空气在管内流动换热时,对其内部插入扰流子进行数值模拟研究,便于对不同尺寸和形状扰流子对换热和流阻的影响进行分析和对比。研究结果表明:圆管内沿轴线插入扰流子的平均换热系数大于光滑圆管;对于插入圆棒式扰流子的情况,绕流子的直径越大,其对流换热效果越好;对于不同形状的扰流子进行对比研究可看出,球形链式扰流子增强换热效果的能力最强,略大于椭球形链式,其次是圆棒式,而椭球式扰流子增强换热效果的能力最弱。
[1]Bergles A E.Heat transfer enhancement-the maturing of the second generation heat transfer technology[J].Heat transfer Engineering,1997(18):47-55.
[2]Bergles A E.Techniques to enhance heat tranfers[M]//Rohsenow W M,Hartnett J P,Chi Y I.Handbook of Heat Transfer.New York:McGraw Hill,1985.
[3]Bergles A E.Application of heat transfer augementation[M].New York:Hemisphere Pub Co,1981.
[4]过增元.对流换热的物理机制及控制.科学通报,2001,45(19):2118-2122.
[5]程伟良,韩晓娟,孙宏玉.质量传递过程中的场协同作用[J].中国电机工程学报,2005,25(13):105-108.
[6]Guo Z Y,Li D Y,Wang B X.A novel concept for convective heat transfer enhancement[J].International Journal of Heat Transfer,1997(41):2221-2225.
[7]Wang S,Guo Z Y,Li Z X.Heat transfer enhancement by using metallic filament insert in channel flow[J].International Journal of Heat Transfer,2001(44):1373-1378.
[8]陈群,任建勋,过增元.流场流动场协调原理及其在减阻中的应用[J].科学通报, 2008, 53(4):489-492.
[9]陶文铨,何雅玲.场协同原理在强化换热与脉管制冷机性能改进中的应用[J].西安交通大学学报, 2002, 36(11):1101-1105.
[10]Tao W Q,He Y L,Liu X,et al.A unified theory for enhancing single phase transport phenomena[C]//Imayishi N,ed.Proceedings of 2001 IAMS International Seminar on Material for Use in Lithium Batteries and Transport Phenomena in Materials Processing.Kasuga:Kyushu University,2001:77-90.
[11]Tao W Q,Guo Z Y,Wang B X.Field synergy principle for enhancing convective heat transfer-its extension and numerical verification[J].Int J Heat Mass Transfer,2002(45):3849-3856.

