火灾下带墙板钢柱抗火承载力的研究

陈 雷, 徐雁飞

(中船第九设计研究院工程有限公司,上海 200063)

0 引 言

钢结构住宅是当前我国住宅现代化、环保化、产业化的一个发展方向,结构构件可采用断面经济的薄壁型材,围护材料可采用轻质节能的新型建材,整个住宅易于实现工厂标准化生产和现场安装。本文研究的低多层轻钢住宅,其骨架结构的梁柱采用高频焊接H型钢,墙楼板采用蒸压轻质加气混凝土板(简称ALC板)。高频焊接H型钢具有生产效率高、翼缘和腹板宽大轻薄、翼缘板平直易于连接等优点;ALC板具有轻质、保温和隔音性能好、施工方便等优点,已在建筑工程中得到推广应用[1-4]。保证结构构件抗火性能达到国家有关规范的要求,是钢结构住宅研发中的重要问题之一。

ALC墙板与钢结构的连接有2种形式：横向连接(连接于柱)和竖向连接(连接于梁)。在工业建筑中的连接方式大多采用横向连接,而在民用建筑中大多采用的是竖向连接。因此,在多层轻钢结构住宅中墙体与柱的连接方式为竖向连接,针对工程实际情况,本文选用ALC板的竖向连接形式进行分析。

在本文所讨论的轻钢住宅中,简支高频焊接H型钢柱的一侧翼缘与ALC墙板连接,认为这一侧翼缘不会受火;同时ALC外墙板与钢柱采用的是竖向连接,ALC板是挂在框架梁上,这样ALC板没有与柱的翼缘有构造连接,因此ALC墙板仅会影响钢柱的升温和截面温度分布,使得钢柱截面的平均温度降低,但同时也造成截面上温度分布不均匀,从而产生温度附加应力[4]。

本文利用通用有限元软件Ansys分析研究有ALC墙板连接的高频焊接H型钢柱抗火承载力分布,同时进一步考虑其他参数对钢柱抗火承载力的影响,并作参数分析。

1 基本假定、模型及判断标准

1.1 基本假定

(1)钢柱翼缘和腹板厚度很小,不考虑其厚度方向上的应力与应变的影响,在模型中用壳单元进行模拟。

(2)钢柱翼缘温度均匀分布,腹板温度呈线性分布[5-6],如图1所示。

图1 截面温度分布加载示意图

(3)高频焊接H型钢内部的温度在各瞬时沿长度方向都是均匀分布的,仅考虑截面上温度不均匀分布,温度分布为二维问题。文献[7-8]研究了沿着钢柱方向温度非均匀分布的破坏情况,指出沿着长度方向的温度非均匀分布相对于均匀分布,提高了柱的临界温度,偏于安全,因此在本文中忽略这种提高效果。

1.2 计算模型

本文的计算模型如图2所示,高频焊接H型钢截面尺寸为H200×200×6×8,柱的高度为2.9 m,作用到柱顶的轴压力NT为：

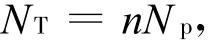
其中n为荷载比;Np为常温下构件有限元计算中的稳定承载力。在柱脚处的约束为强轴方向刚接,弱轴方向为铰接,在柱上部的约束为限制水平方向的位移。在计算过程中考虑了材料的非线性;同时计算过程中考虑大变形效应,引入了几何非线性和构件的初始变形,最大初始变形为构件长度的1/1000。因此,这是一个考虑了材料非线性和几何非线性的问题。

抗火分析采用恒载升温方案,首先在钢柱上作用轴压力NT,计算此时的结构受力变形状态;进而对钢柱的单元节点施加温度荷载(见图1),当构件达到极限状态时认为构件发生破坏,此时截面平均温度即为构件的临界温度。

图2 钢柱有限元模型网格划分图

1.3 判断标准

火灾下结构构件的承载力极限状态的判别标准为：①构件丧失承载力,可以分为强度承载力和稳定承载力,稳定承载力包括整体稳定和局部稳定。②构件达到不适于继续承载的变形。在文献[9]指出柱的变形破坏标准为：

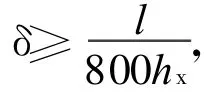
其中,hx为构件的截面高度。

在本文的有限元分析中增加一条判断标准,当认为有限元软件Ansys在分析过程中发散时认为构件达到承载力极限状态。

2 材料参数

材料的基本特性为：钢材材料取Q235钢材,屈服强度为235 MPa(根据文献[1]规定,在进行结构抗火分析中,构件的抗力取材料屈服强度的标准值);弹性模量2.06×1011N/m2,泊松比为0.3;膨胀系数为αs=1.4×10-5/℃。钢材的本构模型采用理想弹塑性双线性模型[10]。

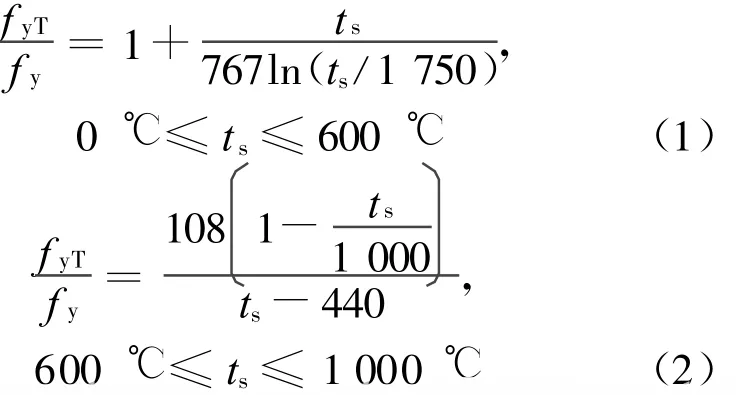
高温下钢材屈服强度采用ECCS[10]的建议：其中,fyT为温度为ts时钢材的屈服强度;fy为常温下钢材的屈服强度;ts为钢材温度。

3 计算结果分析

3.1 轴压钢柱绕弱轴方向的抗火承载力

在柱端施加的轴压力(n=0.4)和温度梯度G=1.33℃/mm作用下的截面温度分布及变形图,如图3所示。截面温度梯度G为钢柱的上下翼缘温差与截面高度的比值[1]。

图3 柱绕轴失稳破坏时的温度分布及变形图

从图3看出,构件破坏时柱的两侧翼缘沿着弱轴方向的变形不一致,从严格意义上来说由于温度梯度G的存在,构件破坏时的变形是弯扭变形,而不是单纯的弯曲变形。这是因为G的存在使得靠近墙板一侧的翼缘温度低,另一侧翼缘温度高,温度的升高使得钢材的屈服强度和弹性模量都开始减小,这样随着温度的升高,两侧翼缘绕弱轴方向的位移开始增大,但由于截面温差G的存在,使得两侧翼缘的变形不一致,远离墙板的一侧翼缘由于温度较高变形较大,靠近墙板一侧的翼缘由于温度较低变形较小,这样最终构件破坏时的变形模式为弯扭变形。

3.2 轴压钢柱绕强轴方向的抗火承载力

为了分析研究钢柱绕强轴发生失稳时的抗火承载力,对模型做了如下修改：限制钢柱发生绕弱轴方向的位移,在柱端施加的轴压力为NT=Npn(n=0.4),温度梯度G=2.00℃/mm。截面变形和截面临界温度分布图略。

4 计算结果比较

关于高温下轴心受压钢构件的抗火极限承载力计算,文献[10]建议了一种方法,即认为高温下轴压钢杆的稳定系数与常温下相同,采用常温下的稳定系数与高温下钢材屈服强度的乘积作为高温下轴心受压钢构件的临界应力(极限承载应力),但假定轴压稳定系数与温度无关是不适宜的。文献[11]中采用了一种高温下轴心受压稳定系数计算的简单方法,并给出极限承载力的验算公式,其计算公式为：

其中,NT为火灾下构件所受的轴压力设计值;φT为高温下轴心受压构件的稳定系数;A为柱的毛截面面积;fyT为高温下钢材屈服强度。

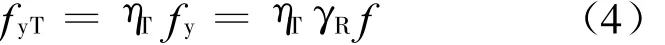
其中,ηT为高温下钢材强度折减系数;γR为钢材抗力系数,γR=1.1。

其中,α为系数,根据构件的长细比和温度按表1所列确定。

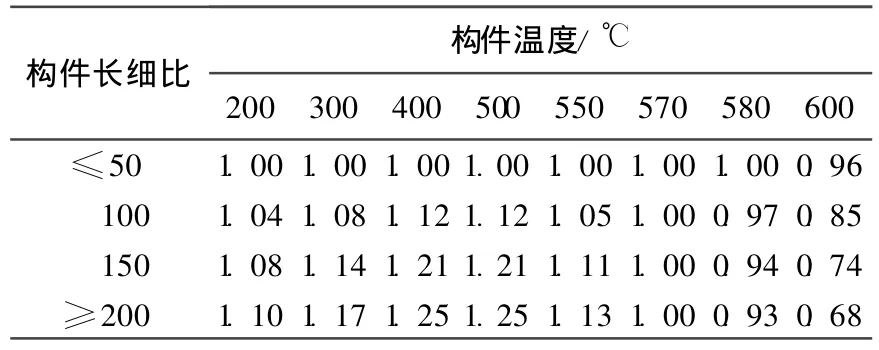
表1 系数α的确定

在常温下,轴心受压柱的极限承载力验算公式[12]为：

本文主要研究的是火灾下的钢柱抗火承载力分析,因此为了和火灾下的公式进行对比,将(6)式中的 f用fy来表示,即

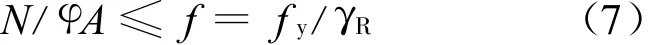
设Np=γRN,荷载比n=NT/Np,结合(3)式和(4)式,可以得出：

本文根据文献[11]中钢柱的抗火极限承载力计算方法,分别计算了不同荷载比n下钢柱破坏时的临界温度tL。

(1)钢柱绕弱轴方向的稳定承载力计算。文献[11]计算结果与有限元结果的对比,见表2所列。

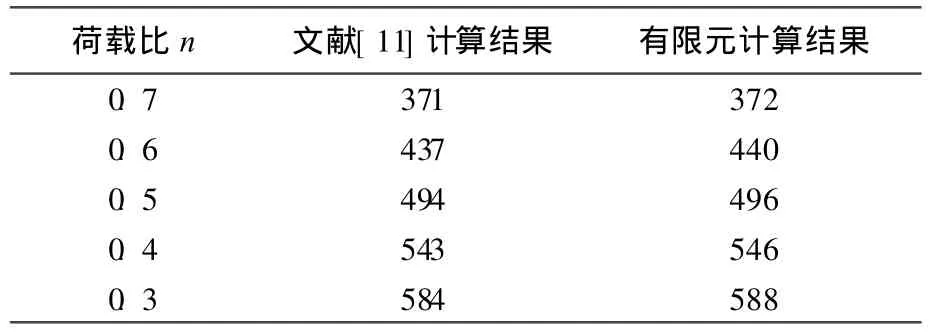
表2 钢柱绕弱轴方向时的tL对比 ℃

(2)钢柱绕强轴方向的稳定承载力计算。文献[11]计算结果与有限元结果的对比,见表3所列。

表3 钢柱绕强轴方向时的tL对比 ℃

(3)比较结果。由上面计算结果的对比可以看出,有限元Ansys计算得到的临界温度与文献[11]计算得到的临界温度很接近,因此可以验证有限元分析是可靠的,可以用来分析有温度梯度G的钢柱截面[1]。

5 参数分析

5.1 不同参数对截面临界温度tL的影响

(1)荷载比n对截面临界温度tL的影响。钢柱分别绕弱轴和强轴方向发生失稳,研究某一温度梯度G下不同荷载比n对于截面临界温度tL的影响 。荷载比 n 变化范围为 0.3、0.4、0.5、0.6 和0.7,计算结果如图4所示。

从图4可以看出,不同的荷载比n对于钢柱截面临界温度tL的影响较大,随着荷载比n的增大,截面的临界温度tL随着减小。

(2)温度梯度G对截面临界温度tL的影响。本文在荷载比n给定的情况下分析不同温度梯度G对于截面临界温度tL的影响,温度梯度G的变化范 围 为 0、0.33、0.67、1.00、1.33、1.67 和2.00℃/mm,计算结果如图5所示。

从图5可以看出,温度梯度G对于截面临界温度tL有不利的影响,在计算钢柱截面临界温度tL必须考虑温度梯度G,文献[11]中不考虑温度梯度G对临界温度tL的影响是偏于不安全的。

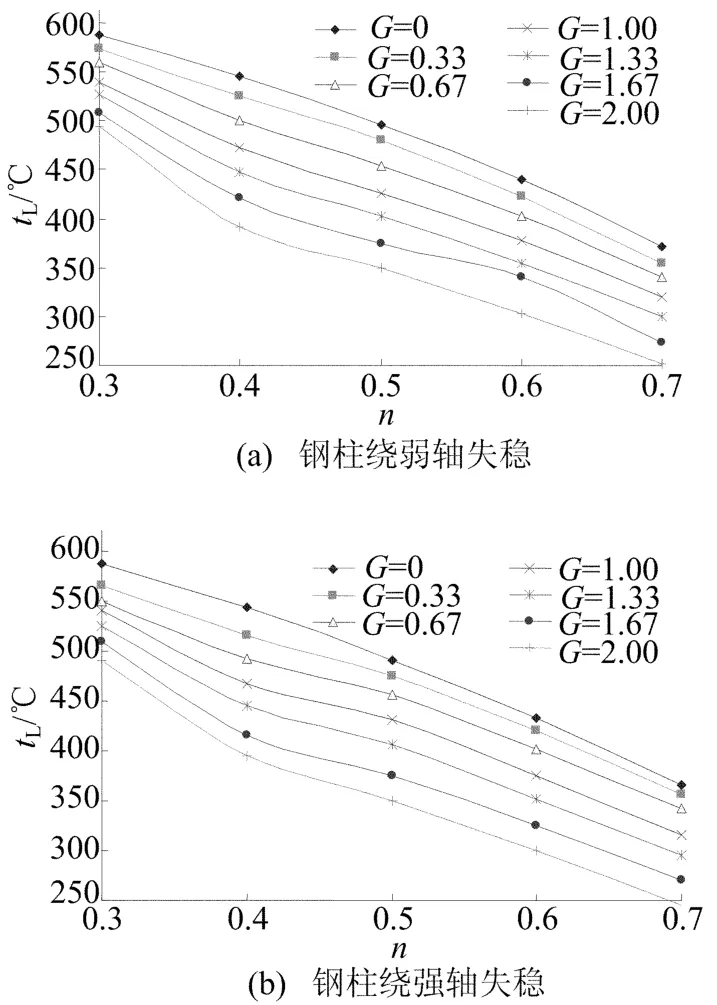
图4 钢柱绕轴失稳n-tL关系

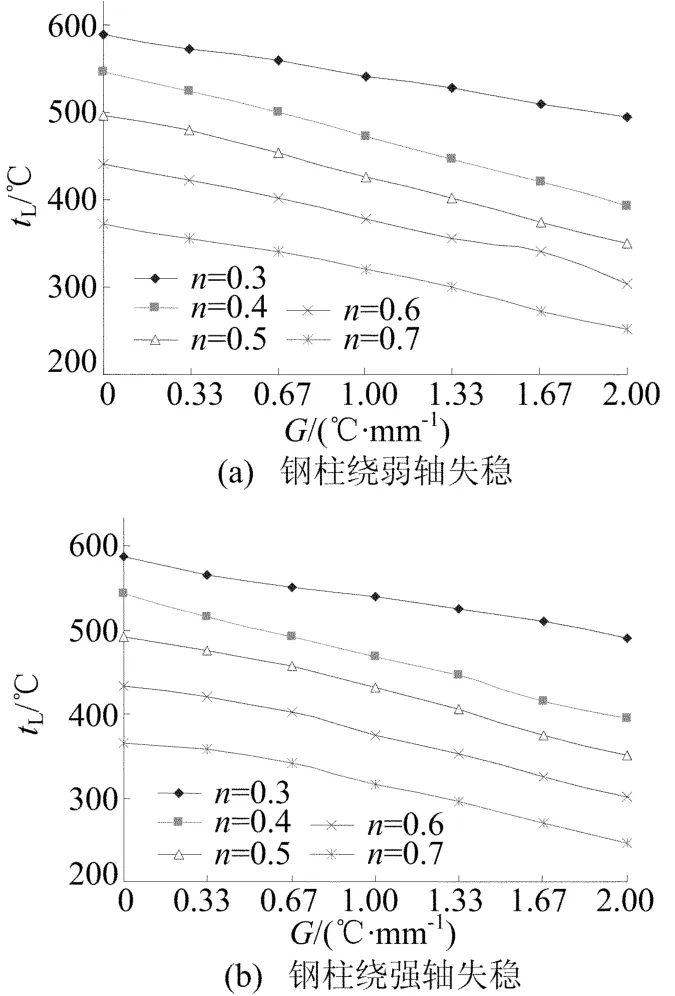
图5 钢柱绕轴失稳G-tL关系

5.2 不同参数对截面温差影响系数β的影响

从上述分析中看出,温度梯度G的存在使得截面承载力降低,因此为了考虑温度梯度G的影响,在(8)式中引入了截面温差影响系数 β,即

当截面温度均匀分布时(即G=0),β=1;当G≠0时,β＜1。截面中的β值越小则对截面临界温度tL越不利。

(1)荷载比n对截面温差影响系数β的影响,如图6所示。

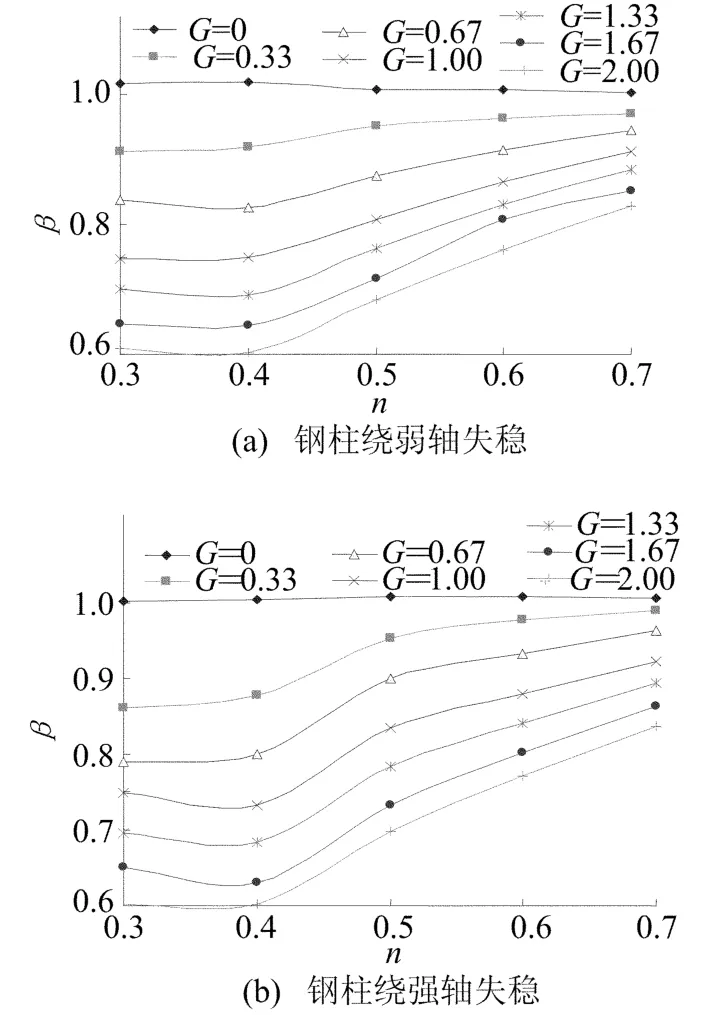
图6 钢柱绕轴失稳n-β关系

从图6可以看出截面温差影响系数β在相同温度梯度G下随着荷载比n的增大而增大。

(2)温度梯度G对截面温差影响系数β的影响,如图7所示。

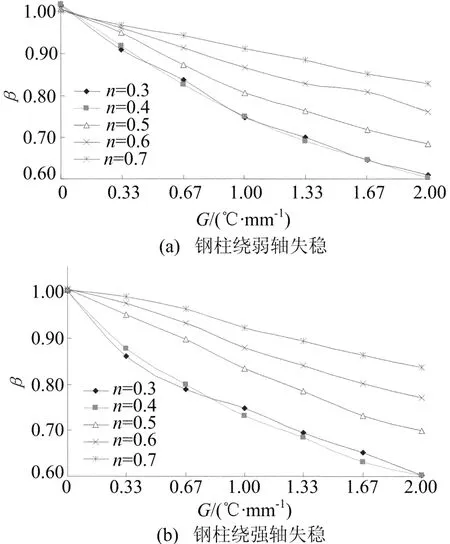
图7 钢柱绕轴失稳G-β关系

从图7可以看出,截面温差影响系数β在相同荷载比n下随着温度梯度G的增大而减小;同时在荷载比n=0.3和n=0.4这2条曲线几乎是重合的。这可能是因为荷载比较小的时候,温度梯度G引起的热弯曲应力也小的原因。

6 结 论

通过对有ALC墙板连接的高频焊接H型钢柱抗火承载力的有限元分析研究,可以得出如下结论。

(1)在一定的荷载比下,钢柱截面温度不均匀(在本文中主要是温度梯度G)所产生的温度应力降低了钢柱的抗火承载力,不考虑截面温度不均匀的计算结果将偏于不安全(现有的规范或规程中不考虑截面温度不均匀分布)。

(2)荷载比是影响构件抗火承载力的重要因素,荷载比的大小将直接决定截面的临界温度。

(3)在钢柱绕弱轴发生失稳时,温度梯度G的存在将会使得构件的变形从弯曲变形变为弯扭变形。

[1]李国强,蒋首超,林桂祥.钢结构抗火计算与设计[M].北京：中国建筑工业出版社,1999：75-102.

[2]王培军,李国强,WANG Yong-chang.约束钢柱抗火性能研究现状[J].建筑钢结构进展,2009,11(6)：20-32.

[3]王卫永,李国强.防火涂料局部破损后钢柱抗火性能研究[J].土木工程学报,2009,42(11)：47-54.

[4]吕俊利,董毓利,刘 涛.柱端不同约束 H型截面钢柱抗火性能研究[J].山东建筑大学学报,2010,25(3)：244-246.

[5]陈 雷,童乐为,陈以一.有A LC板连接的高频焊接 H型钢温度场数值分析[J].钢结构,2005,20(1)：56-59.

[6]陈 雷.多层轻钢住宅高频焊接H型钢构件抗火分析[D].上海：同济大学,2004.

[7]Witteveen J,Twilt L.A critical view of the results of standard fire resistance tests on steel columns[J].Fire Safety Journal,1982,11(4)：259-270.

[8]余志武,丁发兴.钢-混凝土组合结构抗火性能研究与应用[J].建筑结构学报,2010,31(6)：96-109.

[9]GB 9978—1999,建筑构件耐火试验方法[S].

[10]ECCS(European Convention for Constructional Steelwork).European Recommendations for the Fire Safety of Steel Structures[S].

[11]DG/TJ 08-008-2000,建筑钢结构防火技术规程[S].

[12]GB 50017-2003,钢结构设计规范[S].