聚变堆用Nb3Sn超导磁体设计分析
刘旭峰, 杜世俊, 叶民友
(中国科学院等离子体物理研究所,安徽合肥 230031)
0 引 言
未来的聚变堆对磁体的基本要求是能承受大电流、强磁场和大的电流变化率,而目前应用广泛且制造技术已趋于成熟的NbTi超导材料显然已不能满足这个要求。由Nb3Sn材料构成的超导磁体最大特点是可以稳定运行于高的临界磁场和大的电流变化率情况下,因此以Nb3Sn取代Nb-Ti作为聚变堆超导磁体的材料成为必然趋势。
目前,聚变装置中超导磁体的导体一般采用导管内多级绞缆导体,即所谓CICC导体(Cable-In-Conduit Conductor,简称CICC)。在超导电缆外面有一个不锈钢管,其作用是既可以用作冷却剂的压力容器,又可作为电磁力的支撑和传递部件。目前,将Nb3Sn超导线应用于CICC大型超导磁体的设计与制造方面的有关报道不多,本文对Nb3Sn超导磁体设计及关键技术进行了研究,通过设计并制造出国内首个大型CICC Nb3Sn导体的超导模型线圈,并对Nb3Sn导体和磁体的各项性能进行测试。
本文以零维模型为基础对磁体进行分析,通过一系列经典的计算公式得到模型线圈的相关参数,为磁体的工程设计和实验提供依据。
1 磁体设计方案及主要参数
磁体初步设计方案为内径 600 mm,外径860 mm,高度170 mm。线圈由CICC导体绕制而成,为10×10匝,导体总长度约230 m,线圈的整体结构和线圈的冷却回路如图1所示。模型线圈的冷却方式为超临界氦迫流冷却,工作温度为4.2 K,分5个冷却回路,线圈自感为 8.2 mH,最大工作电流约12 kA,线圈储能59 MJ。

图1 线圈整体结构及冷却回路示意图
超导模型线圈由CICC导体绕制而成,该导体结构采用4级绞缆结构,绞缆的配置为(2Sc+1Cu)×3×3×3。即第1级缆为2根超导线和1根铜线扭绞,第2级缆为3个第1级缆扭绞,其余类推,其绞缆配置如图2所示。导体中含超导线54根,铜导线27根,超导和铜导线的外径均为0.83 mm,单根超导线的最大工作电流为220 A。

图2 CICC导体的绞缆配置
为了降低交流损耗,在第3级缆外用0.1 mm的不锈钢带进行花包,另外为了避免在穿管过程中损伤超导线,在最后一级缆外用0.1 mm的不锈钢带进行了半叠包。第4级超导线缆成型后穿入壁厚1.5 mm的316L不锈钢管,通过压方、成型后形成尺寸为13 mm×17 mm的CICC超导电缆,超导电缆的空隙率为33.45%。
线圈在最大工作电流下,截面上的磁场分布状况如图3所示。从中可以看出,线圈上的最大磁场约为4 T且分布在线圈内侧,线圈中心及外侧的磁场要远低于内侧磁场。
对于每匝导体,其不锈钢铠甲截面的拉伸应力为:

其中,B、I和R分别为导体的磁感应强度、电流和半径;A、σ分别为不锈钢铠甲的截面积和拉伸应力。

图3 线圈截面磁场分布
按照最大磁感应强度值计算电磁应力值,得到σ≈228 MPa,而316L不锈钢在4 K温度下的抗拉强度超过700 MPa,所以不锈钢铠甲的强度足够承载电磁载荷。
2 磁体设计分析和计算
2.1 临界电流与温度裕度
电流、温度与磁感应强度是影响超导体的3个重要参数,当超导体处于超导态时,这3个参数有一个上限。如果通过超导体的电流达到这个数值,超导体将从超导态转变为正常态,该电流值称为临界电流。超导体失去电阻进入超导态的温度称为临界温度。进一步的实验表明,外加一个足够强的磁场,超导体将从超导态转变为正常态,该磁场称为临界磁场。
Nb3Sn超导线的临界电流与温度、磁场和应变有关,通常可通过经验公式对不同温度、磁场与应变条件下的临界电流进行预测。为了获得精确的经验公式,常常需要大量的测试数据对经验公式进行充实与修正,以期得到更为完善的结果。
临界电流密度、临界温度和临界磁感应强度可分别由(2)~(4)式求得[1]:

其中归一化参数为:

根据(2)式可求得 Nb3Sn超导线在温度4.2 K、磁场4 T和应变-0.7%下的临界电流Ic=684 A。实际运行时,电流应不超过理论计算值的80%。根据设计方案,超导磁体单根超导线的最大工作电流为220 A,远小于临界电流,磁体是安全的。
温度裕度是指在给定磁场和运行电流下,超导体的电流分流温度Tcs与导体运行温度 Top的差值 ,即

其中,i为运行电流与临界电流的比值。
对于一个运行电流为Iop的超导体来说,当一个暂态能量输入到导体上时,导体温度由 Top升高到 T,当 T<Tcs时,电流仍在超导体中流动,这时没有焦耳热产生。当导体温度满足Tcs<T<Tc时,电流出现分流,一部分电流转移到铜基体中,焦耳热开始产生。当导体温度 T>Tc时,电流全部流入铜基体中。对于CICC导体的设计来说,希望对于暂态的能量输入导体的温度小于Tsc。温度裕度越大,导体越稳定[2]。
由(5)式可以求出模型线圈的温度裕度ΔT=6.68 K,线圈的温度裕度很大,远远超过Nb3Sn超导线圈设计的温度裕度(>1 K),这是因为模型线圈的磁感应强度远小于Nb3Sn超导线的临界磁感应强度(22 T)。
2.2 稳定性裕度
稳定性裕度是导体能够保持或恢复到超导态容许承受的最大暂态能量,通常用单位电缆体积容许吸收的最大能量ΔE来度量。所谓稳定性裕度,意味着当导体的暂态能量小于ΔE时,导体是稳定的[2]。
当温度在4 K附近时,所有固体材料的比热容都变得很小,液氦和超临界氦的比热容比固体材料高出2~3个数量级,因此稳定性裕度主要由冷却剂决定。稳定性裕度的量值取决于导体电缆空间的氦在分流温度和运行温度之间的焓差,其最终的表达式可以写为:

其中,ρhe、che分别为液氦的密度和比热容;fhe为液氦在电缆空间所占的比例,即空隙率。
由(6)式计算得到稳定性裕度为:

2.3 铜超比
CICC导体是准低温稳定的,可以利用Stekly判据来分析导体的稳定性[2]。Stekly判据表示为:

其中,γ为基体材料的电阻率;Ic为超导体中的临界电流;A为基体截面积;h为传热系数;pw为电缆中股的湿润周长。
当T>Tcs时,电流向基体中转移,产生焦耳热。这时需要足够的铜来运载来自导体的电流,并将热量传输到氦中去,以便超导恢复。只要热产生速率小于热移除速率,即α<1,就可以满足这一要求。当T=Tc时,电流将全部流入铜基体中,将Stekly判据改写,从而得到使导体稳定的铜和非铜的比率应满足:

带入相关参数后得到铜超比≥1.5,磁体导体设计的铜超比为2,满足铜超比的要求。
2.4 极限电流
当导体每单位长度焦耳热产生的速率小于或等于从股线到氦的传热速率时,导体是稳定的,得到股线表面的功率平衡方程为[3]:

当焦耳热的产生和热移出相等时,运行电流达到了最大值,该电流称为极限电流,可表示为:
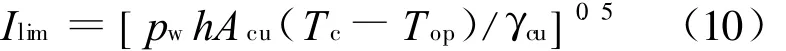
带入相关数据可得到极限电流Ilim=14 kA,磁体设计的最大电流为12 kA,小于其极限电流。
2.5 导体冷却回路液氦压差
模型线圈采用超临界氦迫流冷却,共有5个冷却回路,每个冷却回路的长度约46 m。若氦的质量流率过小,则无法快速地将失超的热量带走;另一方面,若氦的质量流率过大,则又会造成冷却回路两端压差过大,造成制冷机的负荷加大,因此要合理地确定质量流率与氦压差的关系。
冷却回路两端的氦压差可以表示为[4]:
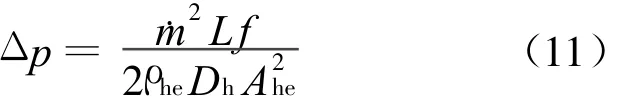
其中,﹒m为质量流率;L为冷却回路长度;f为摩擦系数;Ahe为液氦的截面积;Dh=4Ahe/pw为水力直径。
摩擦系数 f可以写为:
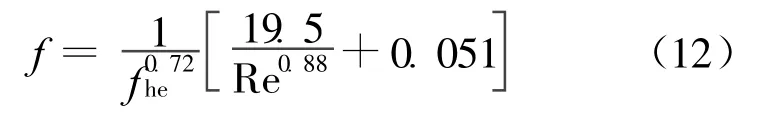
其中,Re=﹒mDh/Ahe为雷诺数,μ为动力黏度。
计算得到的质量流率与氦压差的关系,如图4所示。从中可以看出,随着质量流率的增加,冷却回路两端的氦压差也增加。为维持氦的超临界状态,其压力应不小于 3 bar,因此取入口压力pin=4 bar,出口压力为pout≈3.4 bar。

图4 氦压差与质量流率的关系
2.6 导体失超后的氦气压力
导体失超后,电流流入铜基体形成焦耳热,可能会导致液氦汽化形成氦气。液氦汽化后将在不锈钢铠甲内部产生较大的压力,因此需要对磁体失超后的氦气压力进行计算以确保不锈钢铠甲能承受氦气压力。按保守计算,可以认为整段冷却回路上的液氦全部变成氦气,其压力可表示为[5]:

其中,Jca为电缆空间电流密度;fcu为电缆空间铜所占的比例;γcu为铜的电阻率。
计算可得磁体失超后冷却回路的氦气压力约为18.5 MPa,这是保守的计算结果,实际上因为有失超保护回路,不可能全部冷却回路上的液氦全部汽化。当磁体失超且液氦汽化时,根据18.5 MPa氦气压力下有限元分析计算结果,不锈钢铠甲容器承受的最大应力为535 MPa,小于316L不锈钢材料在4 K下的700 MPa许用应力。从中可以看出,即使失超时液氦全部汽化,磁体也是安全的。
2.7 导体温升与失超保护
导体失超时,产生的焦耳热使导体温度升高,同时失超探测回路在侦测到失超信号后及时动作,将储存在线圈中的能量释放到泄能电阻上,从而有效地保护线圈不受损伤。
焦耳热引起的线圈温升可以用(14)式进行简单估算[6-7]:

其中,I0为线圈最大工作电流;Δ t为失超回路延迟动作时间;ΔT为线圈温升;τ为失超回路的时间常数为铜的平均电阻率分别为铜和Nb3Sn的平均比热容;ρcu、ρNb3Sn分别为铜和Nb3Sn的面积。
根据设计要求ΔT≤150 K,由(14)式可得失超保护回路的时间常数应满足τ≤0.42 s。再根据失超时线圈中钢导线的自身电阻r=15 mΩ和线圈电感L=8.2 mH,可以得到失超回路串接电阻R≥4.5 mΩ。
另一方面,电流衰减过快,则会引起线圈端电压过大,因此导体失超时串入线圈的泄能电阻应合适。导体失超,线圈端电压即为泄能电阻R两端电压,可表示为:

其中,I0为磁体失超时的初始电流,取最大电流12 kA。
根据(15)式和线圈允许的最大端电压Umax=1 kV可得泄能电阻R≤83 mΩ。
由此可得到失超回路串接电阻为:

2.8 交流损耗
超导磁体在稳态运行时,由于电阻为零,所以不存在损耗。由于聚变磁体的特点是电流和磁场不断变化,当电流变化时会在磁体中产生交流损耗。为了保证超导磁体在变化的磁场中能够稳定地运行,磁体设计时应对产生交流损耗有所限定,即小于稳定性裕度[8]。
交流损耗主要分为2种类型:超导细丝中的磁滞损耗和超导股线及各级子缆之间的耦合损耗。相关文献表明,由于超导丝通常很细,细丝中的磁滞损耗很小,可以不予考虑,因此主要分析超导股线中的耦合损耗。
耦合损耗可以用单位体积产生的能量表示为:其中,τ为耦合时间常数;n与股线类型有关,对于圆形股线n=2。耦合时间常数的取值参考了国内外相关装置如KSTAR、EAST等超导磁体,比较了相应的导体尺寸后,确定τ=60 ms。

磁体运行时的电流波形,如图5所示。在磁体电流升至最大值12 kA后,电流以24 kA/s的速度下降至 10.8 kA,再以 12 kA/s的速度下降至9.0 kA,接着以9 kA/s的速度下降至0。电流反向后以 6 kA/s的速度下降至-6.0 kA,再以3 kA/s的速度下降至-12.0 kA。然后以1.5 kA/s的速度上升至-6.0 kA,最后以3 kA/s的速度上升至0。整个过程中对应的最大磁场变化率约8 T/s。

图5 线圈运行电流波形
根据以上放电波形可以求出不同时刻磁体上各处的磁场变化率,为计算简单起见,磁体上各处的磁场变化率取最大值,可以求出磁体耦合损耗为Ec=2266 mJ/cm3。虽然求得的耦合损耗超出了导体的稳定性裕度(1852 mJ/cm3),但这是相对保守的数据。因为线圈上最大磁场变化率仅出现在几个点的位置,大部分位置的磁场变化率均低于该值,尤其在线圈外侧磁场变化率不到最大值的1/2,实际的耦合损耗不会大于导体的稳定性裕度。
3 结果与讨论
Nb3Sn超导磁体的主要参数,见表1所列。
在磁体设计方案中,Nb3Sn超导导体采用4级绞缆结构,超导电缆的空隙率为33.45%、铜超比为2,磁体有5个冷却回路,该导体结构可以满足磁体运行时对液氦冷却回路的要求。
本文根据零维数学模型,对Nb3Sn超导磁体的设计参数进行了详细的分析和计算。从设计分析可以看出,Nb3Sn超导磁体具有较大的温度裕度和稳定性裕度,这一方面是因为Nb3Sn超导体具有较高的临界温度,另一方面则是因为线圈处在较低的磁场环境中。耦合损耗的结果虽略大于稳定性裕度,但计算中磁场变化率取最大值,因此实际的耦合损耗不会大于导体的稳定性裕度。计算结果表明,磁体在设计参数下运行稳定可靠。
在磁体故障态失超情况下,保护回路泄能电阻不仅能快速转移磁体中的能量而且避免快速电流变化产生的过高电压。同时失超后氦气压力计算表明,导体不锈钢铠甲的强度足以承受液氦汽化后产生的压力,磁体运行安全。

表1 Nb3Sn超导磁体的参数
[1]Devred A.IT ER Nb3Sn critical surface parameterization[R].IT ER Organization:Cadarache,2008.
[2]李保增,郭增基.CICC超导体的设计及其稳定性[J].低温与超导,1995,23(2):19-21.
[3]李保增.CICC型超导体运行电流的设计[J].低温与超导,2001,29(1):33-35.
[4]严定传,欧阳峥嵘,李俊杰.CICC超导磁体低温冷却设计[J].低温技术,2007,36(1):21-23.
[5]南和礼.绝热超导磁体失超过渡过程的数值模拟研究[J].低温物理学报,2000,22(4):299-301.
[6]ITER Magnet Group.ITER-D-2NBKXY v1.2(R)[R].ITER Organization:Cadarache,2009.
[7]郭增基,李保增.12T(Nb,Ti)3Sn超导体电流密度的设计[J].低温与超导,1995,23(2):26-27.
[8]李保增,毕延芳,吴维越,等.大型超导电缆交流损耗的计算[J].低温与超导,2000,28(4):13-15.

