基于FPGA和CIS的纸币图像采集及5/3提升小波图像处理方法

肖 军, 肖本贤, 陶运超, 赵梅玲

(合肥工业大学电气与自动化工程学院,安徽合肥 230009)

0 引 言

改革开放以来,随着我国国民经济的快速发展,现钞的流通量得到迅速增长,极大地刺激了银行业的发展;同时ATM 机的普及,对流通的货币质量要求越来越高,纸币清分工作对金融机构来说就显得格外重要。虽然国内将图像处理技术用于纸币清分的研究论文不断出现[1-3],但目前仍然没有达到成熟实用阶段。本文对纸币清分机的图像处理模块进行一些研究,提出了基于FPGA和CIS传感器为核心的硬件平台,并在该平台上用Verilog语言描述实现5/3提升小波算法,完成纸币图像的预处理,为后续实现纸币快速清分奠定了基础。

1 系统硬件资源设计

图像处理模块是纸币清分机的核心部分,也是硬件电路设计的重点。FPGA是系统图像采集控制及处理的核心,控制CIS传感器在工作时所需的各种驱动信号,包括点亮光源信号,CIS启动信号以及时钟信号等;同时FPGA还需要为高速A/D转换器 TLC5540提供转换时钟信号。CIS传感器在FPGA控制下,将每一个像素的灰度值以模拟电压值形式通过串行移位方式传输出来;每个像素的电信号经过信号调理电路输出后与CIS传感器输出的参考电压一同送入差分放大再送往A/D转换器,由A/D转换器将模拟电压转换为数字量送往FPGA,FPGA将接收到的图像信息进行5/3提升小波变换,从而完成图像数据预处理。系统框图如图1所示。

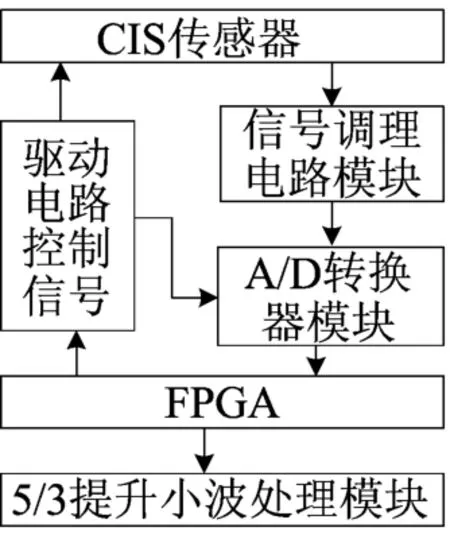
图1 图形采集与处理系统框图

1.1 LT1R183N CIS传感器

CIS传感器即接触式图像传感器,是光电产品中除CCD外最常见的新型光电耦合图像传感器,主要由LED光源、柱状透镜组、CMOS图像传感器等构成,并集成在一个条状方形盒内。其工作原理与CCD类似,但相比较而言,它不需要光学成像系统,就可将“光—机—电”一体化转变为“机—电”一体化,且具有结构紧凑、体积小、价格低、安装方便等优点,广泛应用于高速图像处理、图形式扫描器及办公自动化等领域,近年来在金融设备中也得到了成功应用。

本系统采用的CIS传感器型号是LT1R183N,有效的扫描宽度是183 mm,感光元件密度为200 dpi/100 dpi可选。其光电检测单元和柱状透镜分别对应地排成线阵,能够分别以红、绿、兰及红外光源对图像进行扫描,推荐的时钟频率为8 MHz。该传感器具体工作时序如图2所示。SI为行采集起始信号,在SI脉冲上升沿的下一个脉冲开始一行的采集,在SI脉冲上升沿的第65个脉冲处才是有效信号输出。LEDr/b/g/ir信号决定一行中发光的时间长度,从而决定光照的平均强度。SIG为输出模拟信号。

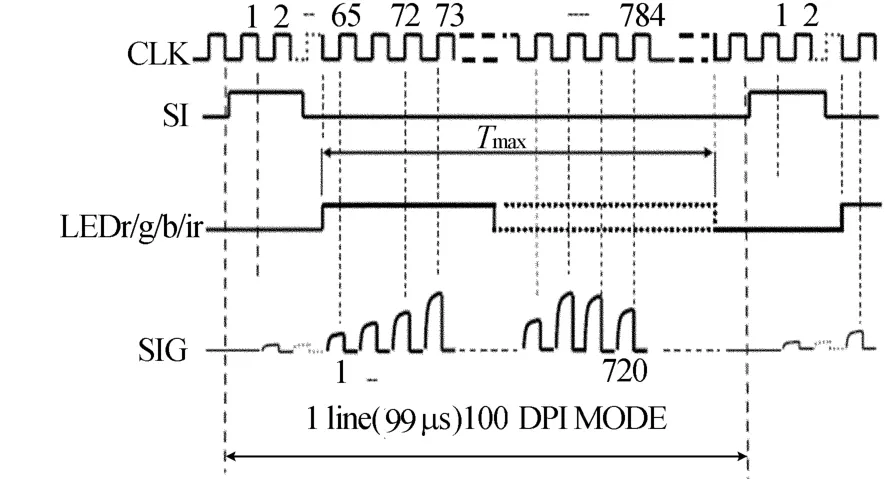
图2 CIS图像传感器工作时序

1.2 Spartan-3系列FPGA

系统采用Xilinx公司的Spartan-3系列FPGA(XC3S200)[4],其有4320个逻辑单元(LC)、216K bit BlockRAM,4个数字延迟锁相环(DDL)和173个用户I/O。与传统微控制器相比,其内部电路功能可在线编程、电路模块并行运行、丰富的I/O资源以及片上集成的多种硬核资源,决定了其在高速数据采集应用中具有不可比拟的优势。系统中利用FPGA为CIS传感器提供满足严格时序要求的工作信号,同时为高速A/D转换器提供转换时钟信号,并实现算法的硬件设计。

2 算法实现方案

近年来,小波变换在信号分析、图像处理、数字压缩等领域取得了具有应用价值的研究成果。本系统在图像采集过程中,由于电机速度干扰、机械振动等因素的影响,采集的图像会存在一定的随机噪声;而CIS传感器数据采样存在自身偏差,这些因素对纸币图像识别有着影响。为减少图像噪声,通常需要进行具有优良效果的图像噪声滤波。在实时图像处理系统中,由于小波变换需要较大的计算量,靠软件无法实现实时需要,其硬件实现具有重大的实际意义。本系统通过FPGA的高度集成和高速处理的特点将小波变换应用于图像处理以满足图像信息实时滤波和压缩。

2.1 提升小波变换

提升小波变换是一种新的构造双正交小波的方法,它使得小波构造摆脱了对傅里叶变换的依赖,可实现整数小波变换,被称为“第2代小波”,其在处理信息量大、效率要求高的应用中具有独特的优势。典型的提升小波变换实现包括分裂(Split)、预测(Predict)、更新(Update)[5-9]3 个步骤。提升框架如图3所示。

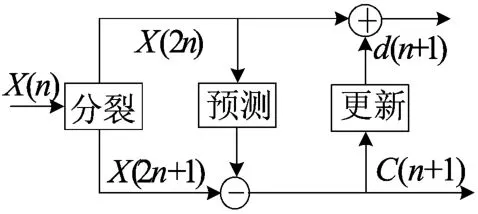
图3 提升小波变换框架示意图

(1)分裂(Split)。将原始信号X(n)划分为2个信号,一般按照下标的奇偶性划分为X(2n)和X(2n+1)两部分,这时每个集合的长度为原始信号的1/2,这一步又被称为“懒惰小波变换”。算子表达式为：

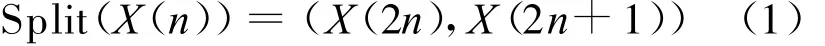
(2)预测(Predict)。在基于原始数据相干性基础上,可以由偶数序列的预测值去预测奇数序列,用C(n+1)表示奇数下标的点与其预测值的偏差,这一步称为“对偶提升”。算子表达式为：

(3)更新(Update)。用偏差C(n+1)修正偶数下标的点,使其保持原始信号的一些特性,这一步称为“主要提升”。算子表达式为：

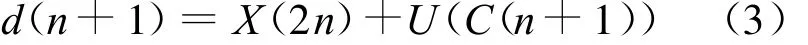
2.2 内嵌延拓5/3小波变换的FPGA实现

2.2.1 内嵌延拓5/3小波变换算法

传统的基于卷积的离散小波计算量大,存储空间要求高,提升小波能有效解决这个问题。目前广泛使用的整数到整数的可逆变换提升小波是5/3小波提升方案,它的优点在于运算复杂度低,所需存储空间小,而且得到的小波系数与传统的小波变换结果相同。5/3小波提升的变换公式如下：

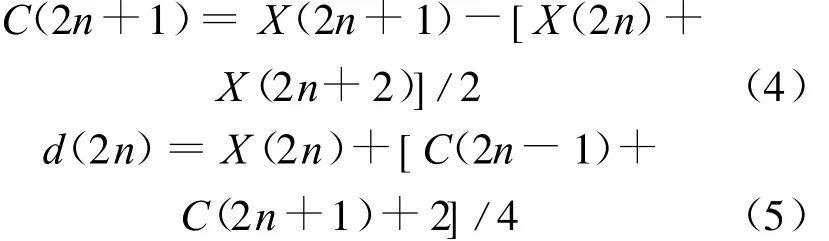
从(4)式、(5)式中可以看出,提升方法可以实现原位运算,即该算法在原位计算各个滤波系数,在原位可以用新的数据替换旧的数据而不需要增加额外的数据存储空间。当重复使用原位提升滤波器组时,就获得了交织的小波变换系数。5/3提升小波变换中的主要计算是加、减运算,而除法运算是除以2和除以4,在硬件中可以通过“右移”操作实现快速运算。上述特性使得小波提升方法容易在基于FPGA硬件电路上实现。

本文小波变换处理对象是硬件系统采集的纸币原始图像数据,一幅纸币图像的行和列都是有限的数据序列,因此对数字图像信号进行小波行变换可以看成是有限长系列滤波的过程。由于序列长度的有限性导致其图像分块出现边界效应。为了消除此边界效应,将延拓过程融合到小波变换过程中,对纸币图像信息的首尾项进行边界延拓处理[10]。以处理8个数据为例,其内嵌延拓过程如图4所示。

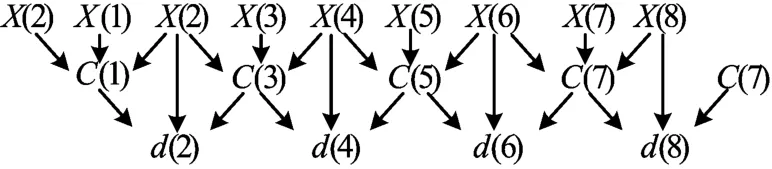
图4 内嵌延拓过程

相应的计算公式如下：

(1)起始阶段,即处理左延拓数据：

(2)正常运行阶段,即

(3)结束阶段,即处理右延拓数据：

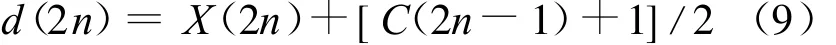
由上述改进算法可以看出,增加一些控制逻辑,可以实现在硬件中无需额外的存储资源,提高小波变换电路的独立性,降低计算的复杂度。

2.2.2 小波变换算法的FPGA仿真实验与验证

本系统以Xilinx公司的FPGA芯片为核心元件,运用Verilog语言实现5/3提升小波变换的硬件设计。在Xilinx ISE 8.2i环境下进行综合和仿真,其部分仿真波形如图5所示。

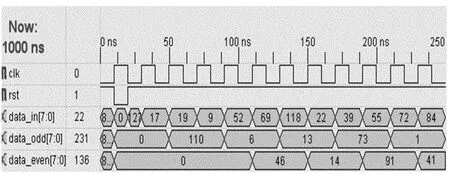
图55/3小波变换算法的部分仿真波形

图5 中,clk为时钟信号;rst为复位信号;data-in为输入数据、data-odd、data-even为输出数据(小波系数),下面来验证硬件设计的可行性。

由仿真波形图可以看出,输入的前10个数据依次是：X(1)=127,X(2)=17,X(3)=19,X(4)=9,X(5)=52,X(6)=69,X(7)=118,X(8)=22,X(9)=39,X(10)=55。

按照内嵌延拓5/3小波变换算法,计算得出：

通过查看仿真波形图可知,硬件设计的正确性得到了验证。同时对硬件设计进行综合,综合结果得出资源情况如下：

Device utilization summary：

……

Selected Device：3s200tq144-4

Number of Slices：63 out of 1920,3%

Number of Slice Flip Flops：63 out of 3840,1%

Number of 4 input LUTs：70 out of 3840,1%

Number of IOs：26

Number of bonded IOBs：26 out of 97,26%

Number of GCLKs：1 out of 8,12%

通过综合结果可知,提升小波易于硬件实现、运算简单、耗费的硬件资源少,并且用FPGA和Verilog语言来描述使得系统的可移植性好。

2.3 纸币图像提升小波处理

本文介绍的提升小波算法处理的对象是纸币图像,经CIS实际采集的每幅纸币图像大小是330(行)×720(列)×8 bit,可以看成是二维灰度图像,在实际的处理中是一维提升小波变换的重复应用,先沿着行方向进行一维提升小波变换,把得到的水平方向的低频子带图像放在左边,高频子带图像放在右边;然后沿着列方向再进行一次一维小波变换,得到的垂直方向的低频子带图像放在上边,高频子带图像放在下边,这样产生大小均为165×360×8 bit的 LL 、HL、LH 、HH 4个子带[11-12],纸币图像的提升小波分解如图6所示。

图6 提升小波分解示意图

实验验证,首先通过清分机系统采集一幅纸币图像,此时纸币的流通速度约500张/min,然后对采集的图像原始数据进行提升小波变换,同时将所有数据通过通讯传给上位机,处理前后图像在上位机中显示,如图7、图8所示。

图7 处理前图像

图8 提升小波处理后图像

在图8中,可以很清楚地分辨出各个不同的子带,看到提升小波变换对能量的集中效果,低频部分集中了纸币图像的大部分能量,而高频部分集中的能量很小,大部分都是灰度值极小的,从而显示出来近似黑色。为了较好地比较纸币图像在变换前后特征是否保持一致,在Matlab中用直方图统计纸币能量,其中横坐标表示的是纸币图像的灰度级,纵坐标是该灰度级出现的频率,结果如图9、图10所示。

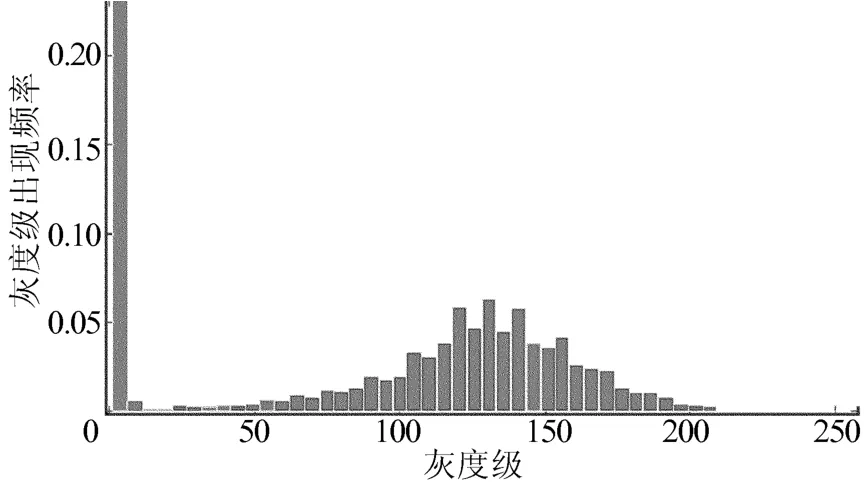
图9 变换前纸币能量分布图

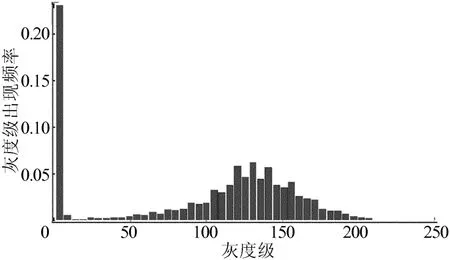
图10 变换后纸币能量分布图

从图9、图10中可以看出,纸币图像在处理前后,能量分布规律大致保持一致,说明采用提升小波在滤波和压缩的同时,依然保持纸币图像的特征,这为以后对纸币的特征处理,如面值、新旧、残缺、真伪的实时与准确判断打下了良好的基础,完成了图像的预处理,尤其是实现了数据量的压缩,压缩后的数据仅为原始数据的1/4。

3 结束语

本文以纸币清分机作为研究对象,提出了基于FPGA和CIS传感器的图像采集系统,并用Verilog语言实现了内嵌延拓5/3小波变换算法,同时进行试验仿真和验证,结果表明硬件设计的可行性。图像采集和5/3提升小波处理模块的目的在于为后续的纸币清分工作提供可靠的数据准备。在后续的实验中,将对纸币的各种特征,如实现版本、面额、面向、污损、粘连币、新旧等级等清分。

[1]刘家锋,刘松波,唐降龙.一种实时纸币识别方法的研究[J].计算机研究与发展,2003,40(7)：1057-1061.

[2]金 野,刘松波,刘家锋,等.一种基于边缘特征的纸币污损检测方法[J].计算机研究与发展,2007,44(2)：258-264.

[3]多 滨,王旭峰.纸币识别系统设计与实现[J].哈尔滨理工大学学报,2008,13(4)：10-13.

[4]田 耘,徐文波.Xilinx FPGA开发实用教程[M].北京：清华大学出版社,2008：15-16.

[5]潘 泉,张 磊,孟晋丽,等.小波滤波方法及应用[M].北京：清华大学出版社,2005：27-29.

[6]卢春晖,王英建,陈 丽.提升小波算法的FPGA硬件实现[J].微处理机,2010(2)：39-41.

[7]Al-Sulaifanie A K,Ahmadi A,Zwolinski M.Very large scale integ ration architecture for integer wavelet transform[J].IET Computers&Digital Techniques,2010,4(6)：471-483.

[8]Hsia C H,Guo J M,Chiang J S.Improved low-complexity algorithm fo r 2-D integer lifting-based discrete wavelet transform using symmetric mask-based scheme[J].Circuits and SystemsforVideoT echnology,2009,19(8)：1202-1208.

[9]姜 婷.基于提升技术的三维小波视频时域滤波方案设计[J].合肥工业大学学报：自然科学版,2009,32(5)：670-673.

[10]戴文伯.基于FPGA的JPEG20005/3提升小波研究与实现[D].武汉：武汉理工大学,2007.

[11]武文波,李 涛,王 琨,等.方向自适应提升小波在遥感图像中的研究[J].中国图象图形学报,2010,15(4)：664-669.

[12]王 昕,刘 畅.基于提升小波变换的图像清晰度评价算法[J].东北师范大学学报：自然科学版,2009,41(4)：52-57.