基于遗传算法的卫星通信干扰资源分配

陈 锋

（海军装备部驻上海地区军事代表局，上海 200018）

遗传算法(Genetic Algorithm，简称GA)是以遗传学理论作为其问题求解模型，利用繁殖、基因交叉和变异，使虚拟的物种在优胜劣汰之后进化成新的物种的一种算法。通常认为GA是模拟生物进化过程的一种新的全局优化搜索算法。[1]近年来，组合优化问题已经成为GA应用最广泛的领域之一。它能够在离散、庞大而有限的数学结构上找出一个解，满足给定的约束条件并使目标函数值达到最大或最小。众多实例表明，GA可以应用于优化作战计划和兵力分配等军事问题的求解。

1 遗传算法的步骤和特点

1.1 遗传算法的步骤

GA的基本步骤有以下三个步骤:

1）随机产生一个初始群体 M(0)，它包括若干个体m(经过编码，模仿生物的染色体，用定长的“遗传”串，如二进制代码表示)。

2）对当前群体M(t)反复执行下面的步骤①和步骤②，直到满足停止条件:

①计算群体中每个个体的适应度值U(m)；

②依概率从 M(t)中选择若干个体，通过选择、交叉和变异等遗传运算产生下一代M(t+1)。

3）如满足停止条件，指定在最后一代群体中适应性最好的个体作为GA的解。

1.2 遗传算法的特点

GA具有以下三个特点:

1）GA最为可贵的特点就是很大通用性，应用范围比较广。这主要是因为:

①它不对参数本身，而是对参数集合进行了编码操作的个体进行处理；

②基本不用搜索空间的知识或其它信息，仅用适应度函数评价个体。适应度函数只需要根据输入计算出可加以比较的非负结果。

2）对巨大搜索空间并行的全局搜索能力。可同时对搜索空间中多个子空间内的解进行评价，减少了陷入局部最优解的可能性，提高了解题速度。

3）利用概率方法引导其搜索朝着搜索空间中接近最优解的子空间移动。看似盲目搜索，实为方向明确的高效搜索。

2 利用遗传算法的卫星通信干扰资源分配算法

随着卫星通信链路以及卫星通信干扰资源的增加，干扰资源分配方案会急剧增加，造成搜索空间爆炸。这种典型的组合优化问题比较适合于使用遗传算法来解决。下面就干扰资源分配中使用遗传算法的步骤进行逐一分析。

2.1 编码

编码采用的是多参数映射方法。每一个体表示一种可能的干扰资源分配方案。为了适合卫星通信干扰的特点及简化计算，这里采用了一维结构对象的十进制整数编码。因为卫星通信干扰的对象有两种，可能是卫星本身也可能是地面站，这里假定卫星数和地面干扰站数均不超过10个，所以如果卫星通信干扰的对象是地面站时，编号直接从11开始，升空干扰站的编号也直接从11开始。假定卫星通信干扰设备数量少于100，所以表示干扰分配方案个体的代码串包括低于100个子代码串，每个子代码串由一个整数组成，每个整数表示一个目标编号。

采用整数编码有两个优点:一是编码长度大为缩短，与二进制编码相比，十进制整数编码长度大为减小；二是计算程序大为简化，避免了二进制编码中的约束算法，加快了系统运行速度。

2.2 初始化群体

群体的个数要根据实际编码时代码长度来确定，这里根据试验一般确定群体规模为20个。当然，初始化群体的20个个体是随机产生并经过挑选的，以使其较为均匀地分布在整个搜索空间的多个子空间。如果干扰设备是地面干扰设备，通信卫星个数为N1，其目标的选择是抽取 0～N1的随机数，否则根据空中干扰设备的个数N2抽取10～(10＋N2)的随机数。

2.3 适应度函数

适应度函数用来评价群体中个体的优劣，其数值是淘汰劣势的标准。它是根据卫星通信干扰的实际应用而不是由GA来确定，采用的方法如下:以单部干扰机的干扰效果为基础，对干扰效果进行划分，利用经验方法，分别为某个干扰方案中指定的若干部干扰机相对于其干扰对象的干扰效果进行评估，并计算出总的干扰效果，然后将这些评估干扰效果的值求和得出该个体的适应度函数值。如果某一个体的适应度函数值较小，则它将成为可能被淘汰的劣势个体。为了便于对适应度函数进行比较排序，其函数值应该非负。

通过上述方法，可将本项应用的最优化问题目标函数转换成可求得最大值的适应度函数。

2.4 单对单卫星通信干扰效果评估及量化经验方法

通常，卫星通信干扰效果评估不能够直接利用按照理论计算得出的数值，而是采用定性与定量相结合的方法，将理论计算得出的数值进一步量化，将其转化为可以实际操作并且方便用于该应用的数值。这里就是采用了这样一种方法，根据干扰机搭载平台类型的不同，分别计算相应的干扰效果。考虑到实际情况，干扰机搭载平台类型只分为地面和空中两种，所以，单对单卫星通信干扰效果评估可以分为四大类。但是，由于地面平台的干扰机只能干扰卫星并且空中平台的干扰机比较适宜干扰地面站，所以，下面只介绍这两种干扰的干扰效果评估方法。

计算干扰效果首先要确定指标，通过比较统一的指标值大小来确定干扰效果。接收机的输入干信比是一个比较常用的计算干扰效果的指标，这里仍然沿用这个指标。

1）地面平台干扰卫星效果计算

卫星通信干扰设备要能对上行信号实施有效干扰，必须满足以下条件:

①上行信号工作频率 Fu(GHz)在干扰设备的可干扰频率范围［fjmin，fjmax］之内；

②干扰设备位于通信卫星的覆球区内，即满足位置条件:

式中，βsj为通信卫星和干扰设备在地球表面上投影间的地心角，可按式（2）计算:

其中，Φj、θj分别为干扰设备的经度（-π≤Φj≤π）和纬度（-π/2≤θj≤π/2）。

③通信卫星接收到的干扰功率和信号功率之比为

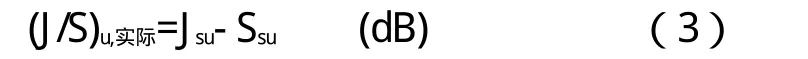
式中，Jsu为通信卫星接收到的干扰功率，可根据卫星通信的线路方程计算:

Ssu为通信卫星接收到的信号功率，可根据卫星通信的线路方程计算:

其中，EIRPj、EIRPt——干扰机和地面终端发射机的有效全向辐射功率(dBW)；

Gsj、Gst分别为卫星接收天线在干扰方向和地面发射机方向上的增益（dB）；

Lj,u、Lt,u分别为上行链路干扰信号和通信信号的传输损耗（dB），可用自由空间传播损耗公式进行计算:

LAj,u,LAs,u分别为上行链路干扰功率的大气损耗（dB）与信号功率的大气损耗（dB），两者可近似认为相等；

Lp为由于抖动和指向精度误差造成的指向损耗（dB）。

Rsj、Rst分别为通信卫星与干扰机和地面终端发射机之间的距离，可按下式计算[2]:

式中，Φsj＝Φs-Φj；

Φst＝Φs-Φt。

其中，Φt、θt分别为地面发射站的经度（-π≤Φt≤π）和纬度（-π/2≤θt≤π/2）。

2）空中平台干扰地面站效果计算

卫星通信干扰设备要能对下行信号实施有效干扰，必须满足以下条件:

①下行信号工作频率 fd(GHz)在干扰设备的可干扰频率范围［fjmin，fjmax］之内。

②机载干扰机对地面通信接收机的仰角要超过通信接收机需要的最小仰角αmin，即满足位置条件:

式中，hj为机载干扰设备的升空高度（km）；

hj,min为由地面接收站天线波束抑制仰角αmin(rad)计算而得的干扰机升空的最低高度(km)，可按下式计算:

其中，βjr为机载干扰设备与地面接收站在地球表面上投影间的地心角，可按下式计算:

式中，Φr、θr、hr分别为地面接收站的经度（-π≤Φr≤π）、纬度（-π/2≤θr≤π/2）和天线架高(km)。

③地面接收站接收到的干扰功率和信号功率之比为:

式中，Srd为地面接收站接收到的信号功率，可根据卫星通信的线路方程计算:

Jrd为地面接收站接收到的干扰功率，可根据卫星通信的线路方程计算:

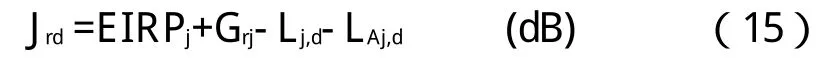
式中，Grj为地面接收机天线在干扰机方向上的增益（dB）；

Ls,d、Lj,d分别为下行链路通信信号和干扰信号的传输损耗（dB），可用自由空间传播损耗公式计算:

LAs,d、LAj,d分别为下行链路信号功率的大气损耗（dB）与干扰功率的大气损耗（dB）。

其中，Rsr为地面接收机与通信卫星之间的距离，可按下式计算:

其中，Φsr＝Φs-Φr;

Φr、θr分别为地面接收站的经纬度。

Rjr为地面接收机与干扰机之间的距离，可按下式计算:

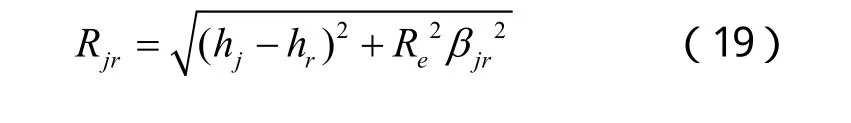
有了干信比，就可以通过其值的大小来量化干扰效果。根据干信比的大小来量化干扰效果的方法比较多，这里根据参考文献[3]和[4]，利用给出的不同误码率情况下，干扰效果等级的不同划分这个条件，将其反解，得出在不同的干扰效果等级下，不同的干信比大小。接下来，只要将实际计算出来的干信比与反解出来的干信比进行比较，如果在哪个范围段内，就将其量化为这个区域较小的那个值。

上述的经验计算方法仅是一种尝试，为了满足不同的实际需要，可以对卫星通信干扰效果评估及量化的经验方法作进一步改进。

2.5 遗传算子

GA以适应度值为依据，反复对群体进行遗传运算，最终得到接近最优解。GA包括三种基本遗传算子:选择，交叉及变异。这三种算子都是在随机扰动下进行，使群体中个体向最优解随机地逼进。此外，还增加了“多对一控制”专用算子。下面分别进行说明:

1）选择

采用最佳个体保存方法(Elitist Model)，即群体中适应度最高的个体不进行交叉和变异而直接复制到下一代中，以保证最后结果一定是历代出现过的最高适应度的个体。

2）交叉

交叉运算把随机选择的父代个体的部分代码进行交换而生成后代新个体。采用一点交叉方法，交叉概率Pe控制交叉运算的频度，这里取Pe=0.5。

3）变异

采用基本变异运算方法，以变异概率Pm，将个体中随机选取的某一整数变为相应的值，具体的操作方法如下所述:如果选取的整数小于10，直接将其变为0，否则直接将其变为10。这里取Pm=0.05。

4）“多对一控制”专用算子

干扰机的数量与其能够干扰的通信卫星数量相等时，则限定按1对1选择目标，不允许多部干扰机干扰同一目标。如果双方数量不相等时，也只是采用有限制的多对一选择干扰目标，只有在此种干扰机的数量大于其能够干扰的目标数时，允许多余的干扰机去干扰已经干扰的目标。例如，4部地面干扰机对2个通信卫星时，只允许1、2或3部干扰机去干扰同一卫星。这里主要是针对地面干扰装备去干扰通信卫星的，因为一般情况下通信卫星的数目比较少。这个专用算子功能是裁减GA搜索空间的大小，减少不合理的目标选择，使干扰机选择尽可能多的目标，从而使总体干扰效果近似最优，但不能保证最优，因为在实际的情况下，干扰目标分配大多数采用的就是近似最优解。

上述专用算子主要是针对卫星通信对抗效能评估设计的。在实际的卫星通信对抗干扰资源分配的过程中，干扰目标的分配要比上述专用算子采用的规则复杂得多。为了满足不同应用需求，可以对专用算子采用的规则作适当的改进和扩充。

2.6 进化代数确定

GA利用适应度函数来判断停止条件，通常以适应度函数的最大值作为GA的停止条件。但是，由于在许多组合优化问题中，适应度函数的最大值就是搜索目标，很难确定。所以GA运算中，如果发现相当数量的个体是同一种类，群体进化趋于稳定，则停止运算。

在利用GA进行卫星通信干扰资源分配的过程中，可以记录历次干扰目标分配方案的最大适应度函数值及对应的进化代数等数据并画出曲线，以此来确定应该进化多少代停止GA。

根据参考文献[5]得出的结论，这里采用进化的代数为20代。

3 仿真结果

下面针对一具体情况，进行仿真，并给出仿真的结果。假设红方现有地面干扰卫星通信装备4部，空中干扰卫星通信装备8部，蓝方现有通信卫星2个，地面站20个，可能的卫星通道数为12个。根据上面给出的利用GA进行干扰资源分配的方法，进行仿真。仿真的结果如表1所示。

表1 仿真结果

对仿真结果进行分析，出现前四位的排列为1011和1101的原因有以下几个方面:一是地面干扰站需要的功率比较大，一部干扰机的效果可能不是很好，需要多部干扰机去干扰同一个通信卫星，这里就出现了三部地面干扰机去干扰第二个卫星的情况；二是卫星的覆盖范围比较广，无论用第二个地面干扰机还是用第三个地面干扰机去干扰第一个卫星，效果都会是一样的。空中干扰机干扰地面站的情况就与地面干扰机不一样了，基本上变化不是很大。这主要是因为空中干扰机受到的限制比较大，且受到地面站在空间上的位置影响比较大，且必须符合升空高度的要求，这里出现最后一位不同也仅是因为第十六个地面站与第十七个地面站在地理位置上差不多，且离地面高度也相差不大这两个原因导致。

上面的仿真结果是在进化20代时给出的，由于这两种分配方案得到的最大适应度函数值是一样的，故暂可认为这两种分配方案都是比较好的分配方案。当然，随着进化代数的增加，得到的最大适应度函数也有可能会发生变化，此时干扰的分配方案也会相应发生变化，所以这里只是给出一个近似的最优解。

4 结束语

在未来战场上，空间资源的争夺战必将愈演愈烈，其中，卫星通信与反卫星通信之间的对抗会首当其冲。对反卫星通信的研究必将涉及到对卫星通信实施电子攻击，对卫星通信信号实施电子干扰，以扰乱其信息的中继转发或接收，在战争期间是完全可行的，也是非常有效的。为了能够在战时更有效地干扰敌方的卫星通信，合理地分配现有的干扰资源将显得更为重要。本文利用遗传算法在解决组合优化问题上的优点，初步提出了一种基于遗传算法进行卫星通信干扰资源分配的构想，希望能够借此对卫星通信对抗的发展有所帮助。

[1]曾宪钊.军事最优化方法[M].北京:军事科学出版社.2005:80-99.

[2]吕海寰,等. 卫星通信系统[M].北京:人民邮电出版社,1990.

[3]邵国培等.电子对抗作战效能分析[M]. 北京:解放军出版社,1998:350-361.

[4]McGuffin B F. Distributed jammer performance in Rayleigh fading[J]. In:MILCOM 2002. Proceedings,7-10 Oct.2002:669-674.

[5]丁慧勇,等. 空战智能仿真系统中遗传算法的遗传代数选择问题研究[A].未来战争与军事系统工程, 北京:军事科学出版社,2003.