小波方法在水资源趋势分析中的能力检验

陈 杰，秦 毅，李怀恩，张 静

（1.北京江河瑞通技术发展有限公司，北京 100097；2.西安理工大学西北水资源与环境生态教育部重点实验室，西安 710048）

水资源作为一个地区甚至国家的发展基础，在国民经济中占有重要的地位。因此，准确并合理地分析水资源变化趋势，从而对未来做出预测，具有重要意义。但由于水文循环的复杂性，其发展演化呈现出高度的非线性，这给预测问题特别是中长期趋势预测带来了很大的困难。小波分析作为非线性科学中强有力的工具，在预测领域中得到了越来越多的应用，各种预测方法层出不穷，特别是小波多分辨分析水文时间序列趋势的应用研究取得了迅速的发展。但从实际应用的做法看，尚存在一些值得讨论的问题。我们知道，形成水文序列趋势的原因很多，有天然状态下自身的机理因素，又有气候变化和人类活动的影响；趋势形态表现出复杂多变性，且这种趋势同时还隐含在其它变化特性之中，如周期性和随机性。因此，仅将小波分析得出的最低频信号视为趋势，它是否真实可靠？随着小波分析的层次提高，一个信号序列的低频部分逐渐显现出来，并由弱到强，但当层次继续升高，以低频信号表达的趋势逐渐变为一条水平直线，那么，实用中哪一层分析结果才是合理的趋势？分析结果受哪些因素影响？本文通过Monte Carlo模拟试验，着重对小波分析趋势的效果进行检验，从而回答上述问题。

1 试验设计

从水文过程的物理成因知，水文物理过程可以表示为趋势成分 A（t）、周期成分 P（t）和随机成分 R（t）的组合：

因此试验时，我们可以用M-C方法，人工生成多种方案的 X（t）如下：

1） X（t）=R（t），纯随机过程。 以此代表水文特征值序列。根据水文序列统计特性，取为正态分布过程和皮尔迅Ⅲ型分布过程。

2） X（t）=P（t）， 纯周期过程。 以此代表水文月径流等周期性变化的时间序列，用正弦函数表示。

3） X（t）=A（t）+R（t）， 随机趋势过程。 以此代表某一时段的水文时间序列，其中趋势过程采用水文上常出现的型式：直线型y1=t、指数型y2=2.5e0.04t和S型，其中 t=1,2,3,…,n。

4） X（t）=A（t）+P（t）+R（t）,显然它是水文序列更一般的型式。

对上述假设水文序列，利用广泛采用的小波多分辨分析方法进行分解与重构，从而得到小波分析的趋势系列。由于上述X（t）序列的趋势型式A（t）已知，这里称其为真实趋势，则可以根据小波分析出的趋势系列对真实趋势A（t）的描述效果，决定小波分解尺度a的大小。这也正是为什么采用M-C方法的原因。设描述效果达到要求时的a=a0，那么在确定a0的同时，观察在a从0变化到a0过程中，小波趋势形状的变化，从而为判定小波分析的趋势提供视觉依据。另外，水文上常采用的直线趋势分析和多项式拟合方法也将同时用来对X（t）进行趋势分析，以便对小波分析的结果进行对比评价。

小波分析所用到的函数 （即小波函数）具有不唯一性，同一个工程问题用不同的小波函数进行分析有时结果相差甚远。小波函数的选用是小波分析应用到实际中的一个难点问题，目前往往是通过经验来选择小波函数。而各种不同类型的小波基函数主要分成两类，一类为正交小波基函数，另一类为非正交小波基函数。根据正交小波与非正交小波的对比研究结果，非正交小波的各个时间尺度小波系数间会受到重复信息的影响，在一定程度上不能很好地反映信号的变化情况。而正交小波因其具有正交性，使得所分解出来的各成分之间两两正交，没有线性相关关系，没有信息冗余。若提取各个时间尺度的相互正交的高低频小波系数，对这些各个层次的系数进行重构，就能清晰地分析出各个层次的信号变化及进行进一步的分析，更好地了解整个信号的变化情况[7]。

本文采用Daubechies-16（DB16）小波进行分析研究。DB16为近似对称的紧支双正交二进小波，它由32个系数标定，没有明确的表达式，其支撑长度和滤波器长度分别为31和32，且尺度函数也是紧支正交的，这使得它们作为多分辨分析的基函数具有很好的局部化特征[7]。将DB16与其他正交小波进行对比试验，得出DB16小波在一定程度上过滤一些 “噪音”，却又严格保持了原信号的特性，而且能揭示出信号的细微变化情况。因此，在以下的分析中采用DB16小波进行探讨。值得说明的是，采用不同的小波分析所得的结果会有所差异，这个问题不在本文的讨论范围。

2 小波多分辨率法识别趋势能力检验

2.1 纯随机序列 X（t）＝R（t）的小波多分辨率趋势分析

本次研究的纯随机序列采用正态分布序列和皮尔逊-Ш分布序列。检验步骤如下：

1） 生成正态 N(0,1)、N(0,50)和N(0,100)的随机序列，样本容量均取n=100。

2）生成皮尔逊-Ш随机序列E(R)=100，变差系数Cv(R)分别为 0.2、0.5、0.8，偏差系数Cs(R)=3Cv(R)，样本容量同样取100。

3）对生成的时间序列进行小波多分辨趋势分析，确定分解尺度a，对重构序列写出趋势方程。

4）对趋势方程的回归系数进行检验，分析结果列于表1。从该表可以看出，对于平稳随机序列而言，无论是正态分布还是偏态的皮尔逊-Ш分布，小波多分辨分析与直线拟合相差无几，得出的趋势也都为0，说明小波趋势分析不受平稳随机因素的影响。

表1 平稳随机序列趋势的小波多分辨分析

2.2 周期序列 X（t）＝P（t）的小波多分辨率趋势分析

本次研究的周期函数取为正弦曲线，如图1所示。首先生成样本容量n=88的正弦周期时间序列P（t），再对该时间序列进行小波多分辨趋势分析，确定分解尺度a，对重构序列写出趋势方程。

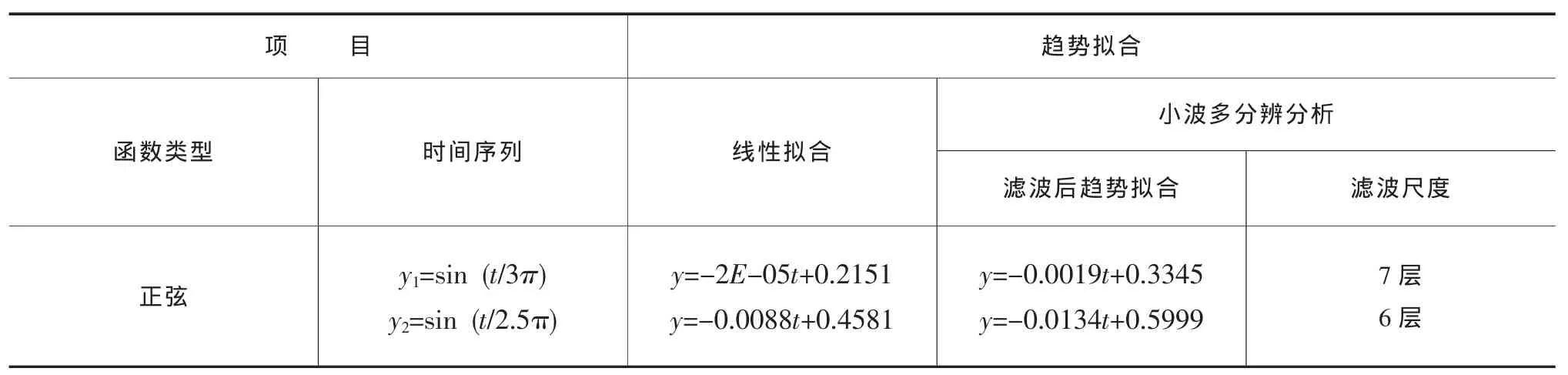
表2 周期序列趋势的小波多分辨分析

从图1及表2可以看出，对于纯周期序列，线性回归和小波多分辨分析结果依然相当，没有大的差别。趋势的强弱只与序列终止时的相位有关，当终止相位与起始相位相同或相差180度时，序列没有趋势，如图1a所示；当相差270度时，趋势最大，如图1b所示，显然这是个伪趋势。同时还可以看到，分解尺度也会随相位的不同而不同。所以，从上面的分析可以得知，若用多分辨小波分析法，以最低频信号视为周期性水文序列的趋势是不可靠的。

2.3 正态噪音时间序列趋势试验

为了进一步了解小波多分辨率分析对时间序列趋势的识别能力，这里仅就确定性的非周期成分和平稳随机成分合成的时间序列X(t)=A(t)+R(t)进行检验。其中R(t)采用生成的正态N(0,σ2)分布随机序列，考虑三种情况，即σ2分别取为1.0、50、100。生成样本容量为n=100。A(t)分别采用水文上常见的趋势成分：

式中 t=1,2,3,…,n。

对X(t)进行小波多分辨趋势分析时，为了反映对趋势成分的识别能力，将识别能力的表征量定义为：

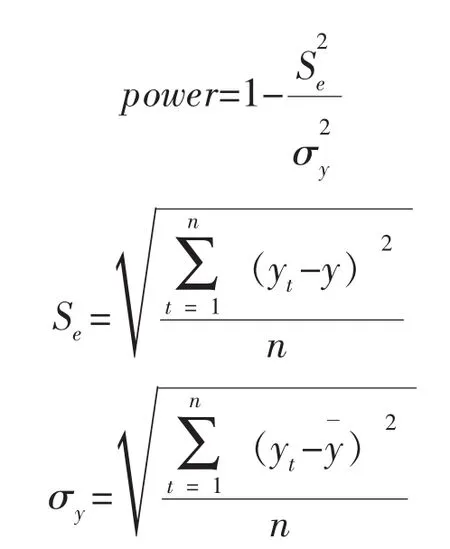
式中：Se——趋势值拟合误差的均方差；

σy——趋势值的均方差；

yt——趋势真值；

y——趋势方程给出的拟合值；

n——趋势值序列的长度。

识别能力的表征量power的取值域为0燮power燮1，其值越接近1，识别能力就越好。

正态噪音序列趋势检验结果见图2和表3。

在图2中，我们可以看到小波多分辨分析和最小二乘法分析所得结果的不同，不管确定性成分是线性还是非线性趋势，小波多分辨分析识别时间序列趋势的能力都很强，可以将X(t)中的确定性成分几乎完全识别出来。根据表3的蒙特卡洛试验得知，与常用的趋势分析方法比较，对于含有确定趋势成分的正态随机序列而言，与线性回归和多项式拟合趋势分析法比较，三者中小波多分辨趋势分析法表现最好，其次为多项式拟合。这说明小波多分辨分析在频域中分析趋势比其他方法在时域中分析趋势更具有优势，同时小波多分辨分析所具有的时频局部化特征，能够合理地反映出时间序列在时间域中的变化特点，因此更能准确地捕捉时间序列的发展演化规律 （如图2c所示）。

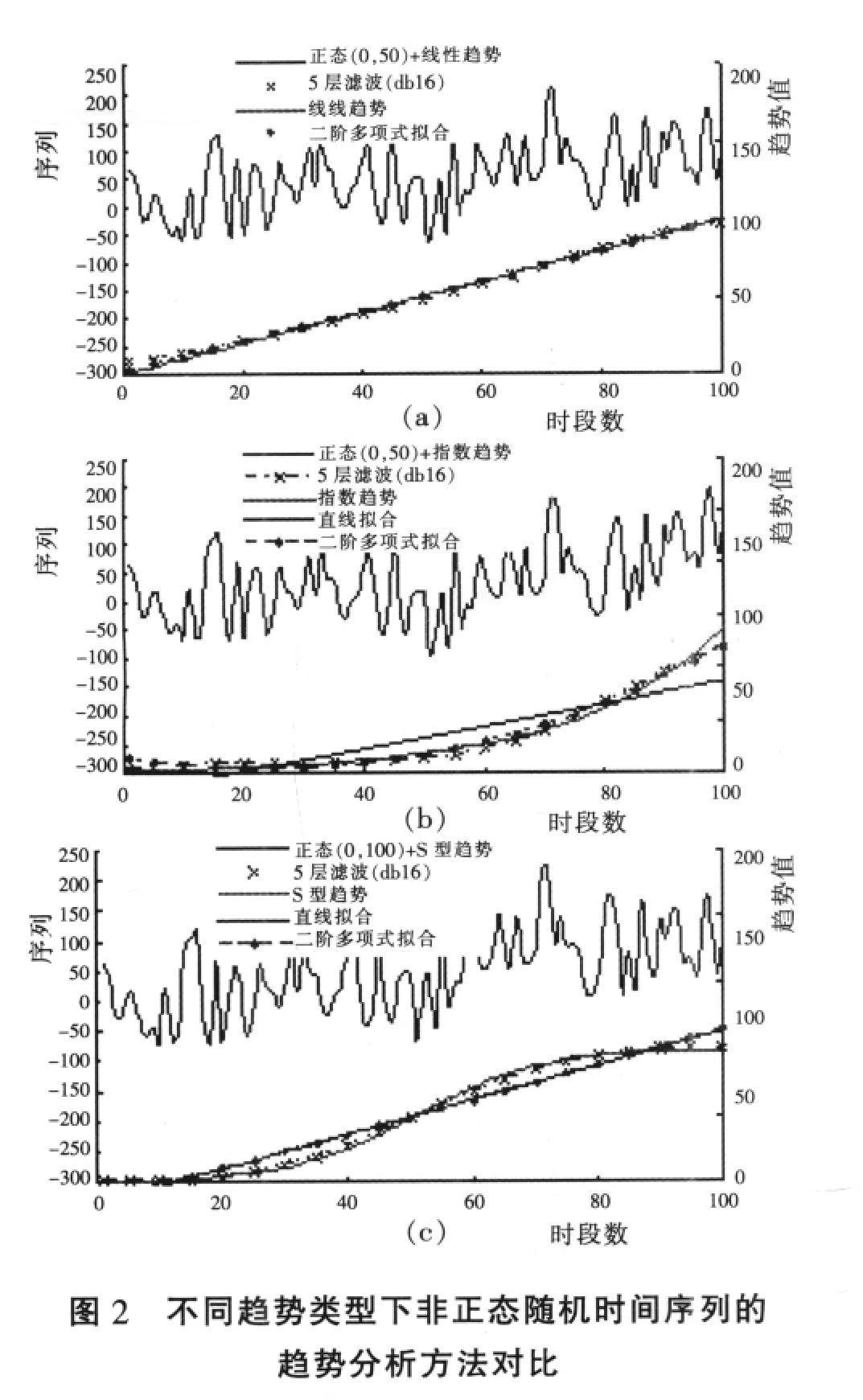
需要强调的是，小波分析所认定的序列趋势是系列中某一尺度a所对应的低频部分，如果趋势序列本身包含有很陡的变化 （突变或跳跃），那么在多尺度小波变换的低频部分中，显示的信号则越来越不像原始信号，因为它将信号本身的陡峭变化当作高频滤掉了。这就是为什么在指数型趋势中，小波趋势分析的结果偏差相对较大的原因（见表3）。这一结果也告诉我们，在用小波进行趋势分析前，应分析序列中是否存在突变，以保证小波趋势分析对水文物理过程的正确反映。

2.4 非正态噪音时间序列趋势试验

一般而言，水文随机分布的统计特征是偏态的。这里将X(t)的随机成分R(t)取为皮尔逊Ⅲ型（PⅢ），其统计参数为：均值 E(R)=100，变差系数Cv分别取 0.2、 0.5、 0.8，偏态系数 Cs=3Cv，样本长度n=100；趋势成分 A(t)的生成方法同“2.3”节的正态噪音时间序列。试验分析方法同上。限于篇幅，图3仅给出部分试验的结果，详情见表4。

对非正态噪音趋势成分系列，在直线型趋势情况下三种趋势分析方法都是稳健的，相差无几。对指数型趋势情形，线性拟合最差，二阶多项式拟合则要比线性回归好得多，而小波多分辨分析趋势还要优于多项式拟合，其所具有的时频局部化特征更能反映趋势的真实情况，这可从图3c中的S型趋势分析看出。小波多分辨分析所具有的时频局部化特征的优点是非常明显的，能够把整个时间序列的趋势变化比较完整地反映出来，而线性回归和二阶多项式拟合仅仅是对趋势变化的最小二乘近似逼近。这说明小波多分辨分析比线性回归、多项式拟合具有更强的适用性，且与所给的趋势类型无关。另外，从表3、表4可以看出，对于给定的趋势线类型，小波趋势分析对正态噪音或非正态噪音的识别能力相当，也即小波趋势分析能力与序列服从的分布类型无关。这两个特点使得小波多分辨分析在水文时间序列的分析上，具有更强的实用性。

2.5 X(t)=A(t)+P(t)+R(t)序列趋势试验

针对更一般的情况，模拟生成随机水文序列。这里将X(t)的随机成分R(t)取为皮尔逊Ⅲ型（PⅢ），其统计参数为：均值E(R)=100，变差系数Cv取0.5，偏态系数Cs=3Cv，样本长度n=100；趋势成分A(t)的生成方法同“2.3”节的正态噪音时间序列；周期成分采用P(t)=100+50sin(t/pi)，趋势分析的试验方法同上。限于篇幅，图4仅给出部分试验的结果，详情见表5。

从图4和表5可以清晰的看出，在同等情况下，小波多分辨趋势分析方法具有很强的识别能力。这也再一次说明小波多分辨分析比线性回归、多项式拟合具有更强的适用性，且与所给的趋势类型无关。对于给定的趋势线类型，小波趋势分析对正态噪音或非正态噪音的识别能力相

当，也即小波趋势分析能力与序列服从的分布类型无关。

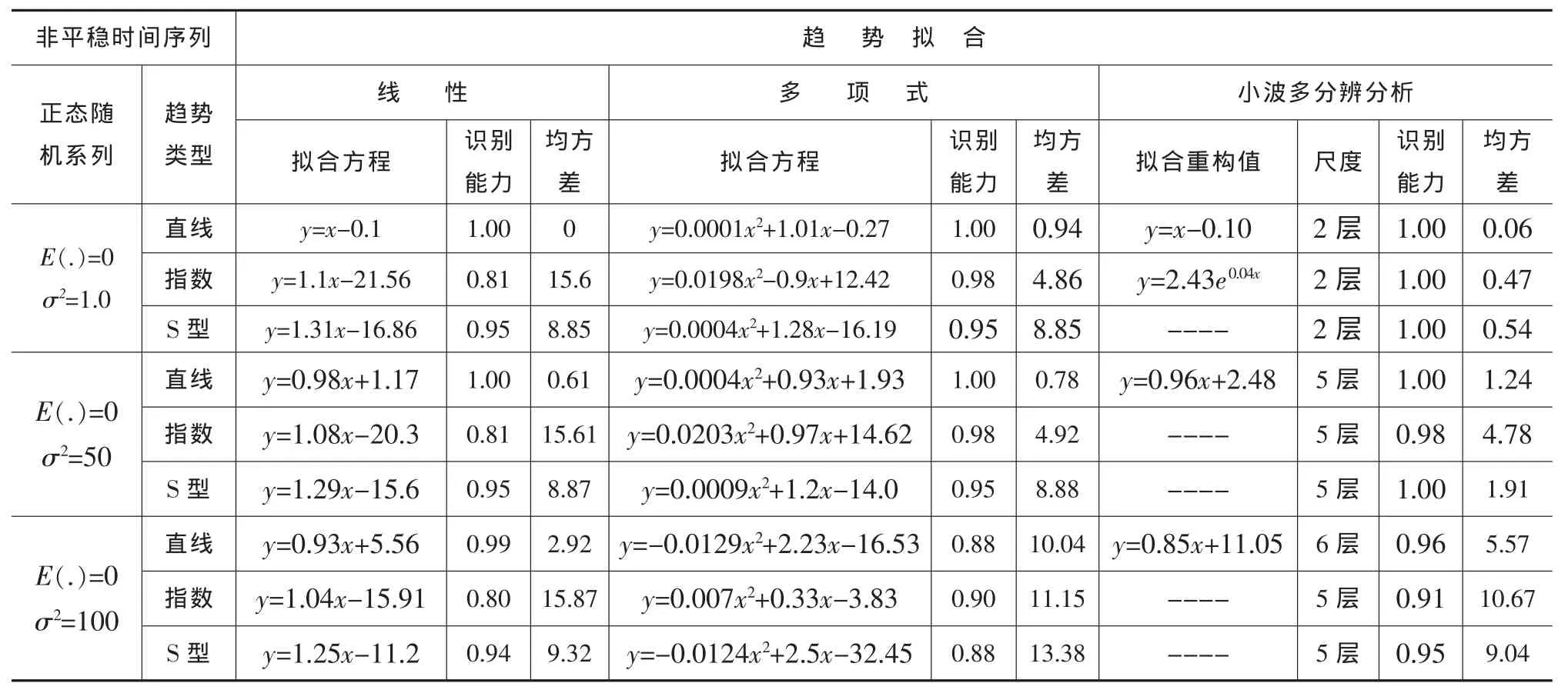
表3 不同趋势类型下正态随机序列的小波多分辨分析

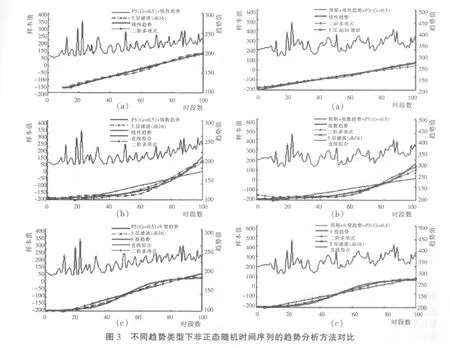
表4 不同趋势类型下各种分析非正态随机时间序列的趋势方法对比

表5 不同趋势类型下各种分析非正态随机时间序列的趋势方法对比

3 关于分解尺度

从表1、表2、表3和表4可以看到，小波多分辨分析的识别能力是最稳健的，即识别能力并不随序列方差的增大而发生显著的降低，但分解尺度却随序列性质的不同而变化。当序列为纯随机时，分解尺度随方差的增加而加大，一般要在a=7以上。这其实是因为序列的方差改变体现在序列高频成分的加强，而高频部分恰恰可以通过调节尺度因子a来实现高频滤波。所以实用中，只要进行高尺度的多分辨分析，就可以比较明显地反映序列的趋势而又不失代表性。当序列为部分随机时，尤其是随机成分所占比例不大时（均值较小），则a的大小与Cv无关，一般a=5，同时，根据对a的跟踪对比发现，多分辨分析的分解尺度a=5是生成时间序列被分解到趋势线接近光滑且没有大的波动时（接近单增或是单减）所对应的尺度，因此，它可作为判定小波分析趋势的视觉依据。由于水文序列中的随机成分所占比重取法准确确定，实用中可以考虑a取5～6。

4 应用实例

为检验本文所描述的小波多分辨分析技术在水文趋势性分析中的应用效果，现采用渭河下游咸阳水文站及泾河张家山水文站1961～2001实测年径流资料进行水文时间序列趋势分析说明。首先，对原始实测年径流值X(t)的距平系列dx(t)（去除各种成分的量级影响）进行周期分析，并重构确定性周期成分P(t)，然后在原实测系列中减去周期成分，再利用其差值dx(t)-P(t)进行小波多分辨趋势分析。由于随机成分所占比例不大，取调节尺度因子a=5，且观察得到实测水文时间序列被分解后的趋势线接近光滑，没有大的波动，因此可以认为这就是所要提取的趋势成分A(t)。对比分析结果如图4和图5所示。

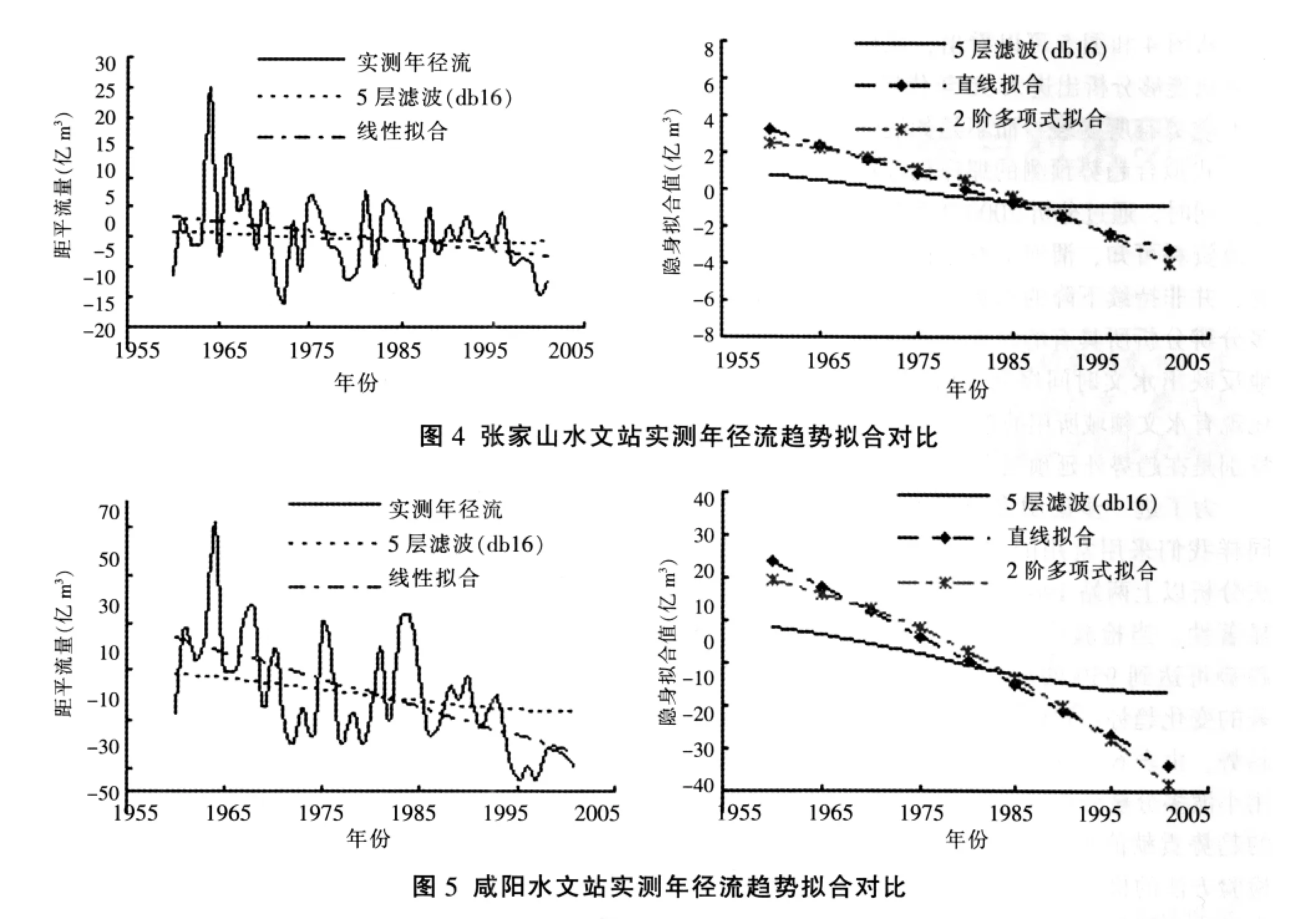
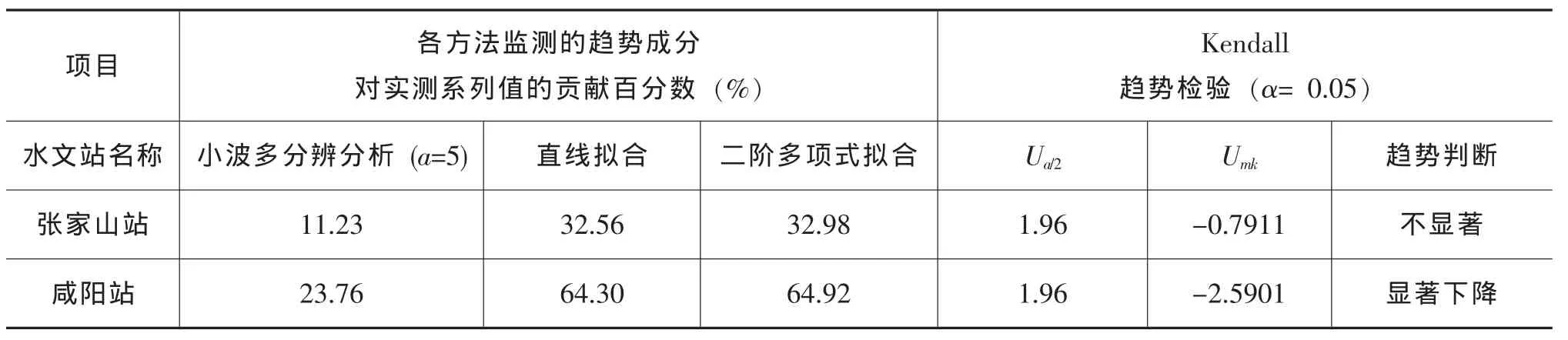
表6 渭河下游实测年径流趋势分析对比

从图4和图5可以看出，采用小波多分辨分析方法能够分析出进入90年代后，实测年径流下降的趋势有所变缓，而不是如线性回归或者二阶多项式拟合趋势预测的那样仍存在继续下降的趋势。同时，通过分析2000年后渭河下游实测的年径流资料可知，渭河下游年径流量为平稳发展演变，并非持续下降的态势。这也从侧面说明小波多分辨分析所具有的时频局部化特征，能够合理地反映出水文时间序列在时间域中的变化特点，比现有水文领域所用的趋势分析方法更具可靠性，特别是在趋势外延预测上。

为了进一步说明多分辨分析方法的合理性，同样我们采用常用的Mann-Kendall趋势检验方法分析以上两站1961～2001年时段的变化趋势的显著性。当检验值的绝对值大于1.96时，变化趋势可达到95%的信度检验，因而认为存在显著的变化趋势；正值表示增大趋势，反之为减小趋势。由表6可以看出，张家山站实测年径流采用小波多分辨分析方法在剔除周期成分后所检验的趋势贡献值为11.23%，与Mann-Kendall趋势检验方法的检验结果是一致，其发展趋势主要是由于水文循环的周期演变引起的。这也从侧面说明了，对于存在确定性周期成分的水文时间序列而言，在进行趋势分析之前，应先剔除周期成分，否则，将会得出如张家山站采用直线拟合分析所得的趋势值贡献达到32.56%，而Mann-Kendall趋势检验却不显著的错误结果。实际上，如前文所述，周期成分的存在会产生伪趋势，而当前在水文领域对水文时间序列进行趋势分析并进行预测时，并没有剔除周期成分再进行分析预测，而是直接拟合趋势分析预测。这种做法显然是不合理。另外，咸阳站小波多分辨趋势分析，趋势贡献值仅为23.76%时，对应的Mann-Kendall趋势检验为显著下降，两者吻合比较好。可见，采用小波多分辨趋势分析的定量方法和Mann-Kendall趋势检验的定性分析方法相结合的模式可以得到比其他方法更合理的结果，其结果也更可靠。

5 结论

1）Monte Carlo模拟试验表明，用小波分析得出的某一尺度a所对应的低频信号作为时间序列的趋势是可行的。

2）小波多分辨分析在频域中分析趋势比其他方法 （如线性回归或多项式拟合法），在时域中分析趋势更具有优势，同时小波多分辨分析所具有的时频局部化特征，能够合理地反映出时间序列在时间域中的变化特点，因此更能捕捉时间序列的发展演化规律。

3）小波趋势分析的识别能力与所给定的趋势线类型及时间序列所含噪音的分布类型无关，只要进行有限尺度的多分辨分析，就可以比较明显地反映序列的趋势而又不失代表性。

4）一般分解尺度a的选择取决于序列随机成分所占比重，比重越大，a值越大。实用中可以考虑a取5～6。过度加大a值，将使分析出的趋势失真。

5）由于小波方法是以滤去高频信号为手段分析趋势，周期成分或突变成分的存在都将影响小波多分法分析趋势的可靠性，因此，在对实测序列进行趋势分析前，应首先剔除这些成分。

[1]李贤彬,丁晶,李后强.水文时间序列的子波分析法[J].水科学进展,1999,10(2):144-149.

[2]王文圣,丁晶,向红莲.小波分析在水文学中的应用研究及展望[J].水科学进展,2002,13(4):515-520.

[3]薛小杰,蒋晓辉,黄强,王煜.小波分析在水文序列趋势分析中的应用[J].应用科学学报,2002,20(4):246-248.

[4]蒋晓辉,刘昌明,黄强.黄河上中游天然径流多时间尺度变化及动因分析[J].自然资源学报,2003,18(2):142-147.

[5]高卫平,秦毅,黄强,郑学萍.唐乃亥流域近期降雨径流特性变化分析[J].西安理工大学学报,2005,21(4):429-432.

[6]程正兴.小波分析算法与应用[M].西安:西安交通大学出版社,1998.

[7]胡昌华,张军波,夏军,张伟.基于MATLAB的系统分析与设计[M].西安:西安电子科技大学出版社,1999.

[8]金光炎.水文水资源随机分析[M].北京:中国科技出版社,1993.